Максвелове једначине

Амперов закон је физички закон који изражава чињеницу да магнетно поље настаје као последица кретања електричних набоја.

Приказ електричног поља које окружује позитивни (црвено) и негативни (плаво) електрични набој.

Приказ електричног поља између два тачкаста електрична набоја.

Поларизовани диелектрични материјал.

Радијално (попречно) електрично поље позитивне кугле.

Магнетно поље је простор око природних и вештачких магнета и унутар њих у којем делују магнетске силе.

Магнетно поље прстенастог магнета.

Максвелове једначине су основне једначине електромагнетизма. Назив су добиле по шкотском физичару Џејмсу Максвелу који је 1864. године објавио први пут рад са једначинама које објашњавају електромагнетске појаве. Овиме је објашњено јединство електричног и магнетног поља и њихова узрочно-последична повезаност. Неке од ових једначина су биле познате и пре овог рада, али их је Максвел први објединио и допунио својим открићима. Поједине једначине су познате и под називима Гаусов закон, Гаусов закон магнетизма, Фарадејев закон и Амперов закон (са Максвеловом исправком). Овај скуп једначина описује електрично и магнетно поље у простору и њихову зависност од густине наелектрисања и електричних струја. Неки пут се овом скупу придружи и Лоренцова једначина. Ове једначине описују свет електромагнетних интеракција у макроскопском свету и зову их једначинама класичног електромагнетизма.

Приказ једначина

За разумевање следећих једначина потребно је познавати основе векторске анализе. Максвелове се једначине могу приказати у диференцијалном и интегралном облику. Еквиваленција између ових облика заснива се на Стоксовој и Гаус-Остроградски теоремима. Такође постоји и четвородимензионални облик који се користи у теорији релативности и квантној електродинамици.

Универзални облик Максвелових једначина описује електромагнетне феномене у вакууму, а у диференцијалној форми (у СИ систему) гласи:

$\nabla \cdot \mathbf {E} ={\frac {\rho }{\epsilon _{0}}}$

$\nabla \cdot \mathbf {B} =0$

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$

$\nabla \times \mathbf {B} =\mu _{0}\cdot \mathbf {J} +\mu _{0}\cdot \epsilon _{0}\cdot {\frac {\partial \mathbf {E} }{\partial t}}$

где је:

$\rho \$ - густина електричног набоја или количина електричног набоја по јединици запремине,

$\mathbf {J} \$ - густина електричне струје, ток електричног набоја по јединици површине у јединици времена,

$\epsilon _{0}\$ - диелектрична константа вакуума (пермитивност),

$\mu _{0}$ - пермеабилност вакуума, а једнака је:

$\mu _{0}={1 \over {\varepsilon _{0}\cdot c^{2}}}$

где је $c\$ брзина светлости.

У Максвеловим једначинама имплицитно се претпоставља да вреди једначина континуитета:

${\partial {\rho } \over \partial t}+\nabla \cdot \mathbf {J} =0$

Ово је заправо закон очувања набоја. За сваку затворену повшину у простору вреди да је ток струје која пролази кроз ту затворену површину једнак негативној промени количине набоја у том простору.

За потпуни опис електромагнетских феномена поред Максвелових једначина нужна је и једначина за Лоренцову силу, како би се из поља могла одредити сила:

$\mathbf {F} =q\cdot (\mathbf {E} +\mathbf {v} \times \mathbf {B} )$

Сажети приказ Максвелових једначина у СИ јединицама

диференцијални облик	повезујућа теорема	интегрални облик
Гаусов закон: извор електричног поља је електрични набој.	Гаусов	Електрични ток кроз затворену плочу једнак је укупном електричном набоју у њеној унутрашњости.
$\nabla \cdot \mathbf {E} ={\frac {\rho }{\epsilon _{0}}}$	$\Leftrightarrow$	$\oint _{\partial V}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =\int _{V}{\frac {\rho }{\epsilon _{0}}}\mathrm {d} V$
Магнетно поље нема извора (не постоје магнетски монополи).	Гаусов	Магнетни ток кроз било коју затворену површину једнак је нули.
$\nabla \cdot \mathbf {B} =0$	$\Leftrightarrow$	$\oint _{\partial V}\mathbf {B} \cdot \mathrm {d} \mathbf {A} =0$
Фарадајев закон индукције: свака промена магнетног поља ствара електрично поље.	Стоксов	Интеграл вектора електричног поља по затвореној кривој једнак је негативној промени по времену магнетног тока обухваћеног том кривом.
$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	$\Leftrightarrow$	$\oint _{\partial A}\mathbf {E} \cdot \mathrm {d} \mathbf {s} =-{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{A}\mathbf {B} \cdot \mathrm {d} \mathbf {A}$
Проширени Амперов закон: око проводника којим тече електрична струја индукује се магнетно поље, али и свако промењиво електрично поље ће индуковати магнетно поље.	Стоксов	Интеграл вектора јачине магнетног поља по затвореној кривој једнак је збиру струје и временске промене електричног тока обухваћених том кривом.
$\nabla \times \mathbf {B} =\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}$	$\Leftrightarrow$	$\oint _{\partial A}\mathbf {B} \cdot \mathrm {d} \mathbf {s} =\int _{A}\mu _{0}\mathbf {J} \cdot \mathrm {d} \mathbf {A} +{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{A}\mu _{0}\epsilon _{0}\mathbf {E} \cdot \mathrm {d} \mathbf {A}$

У горњим једначинама кориштени су симболи СИ мерних јединица :

Симбол	Значење	SI јединице мере
$\mathbf {E}$	електрично поље	волт по метру или, њутн по кулону
$\mathbf {H}$	магнетско поље	ампер по метру
$\mathbf {D}$	електрична индукција	кулон по квадратном метру
$\mathbf {B}$	магнетска индукција	тесла, или, вебер по квадратном метру
$\ \rho \$	густина наелектрисања	кулон по кубном метру
$\mathbf {J}$	густина електричне струје	ампер по квадратном метру
$\mathrm {d} \mathbf {A}$	одсечак површине по којој се интеграли	квадратни метар
$\mathrm {d} V\$	део простора обухваћеног затвореном површином S	кубни метар
$\mathrm {d} \mathbf {l}$	део контуре која окружује површину S	метар
$\nabla \cdot$	оператор дивергенције	по метру
$\nabla \times$	ротор оператор	по метру

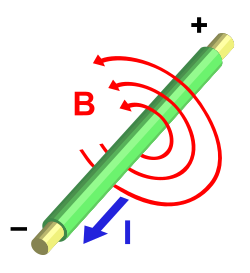
У табели су наведене основне мерне јединице, али често се те физичке величине изражавају и у другим јединицама. Други закон, закон магнетског флукса, наводи чињеницу да магнетских монопола у природи нема. Постоје само диполи а једини извор магнетног поља је електрична струја и променљиво електрично поље. Фарадејев закон показује, да је променљиво (нестатичко) магнетно поље (B) узрок настанка електричног поља.

Објашњење Максвелових једначина

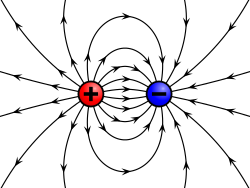
Прва једначина говори да је електрични набој извор (или понор) електричног поља. Укупни електрични ток кроз затворену површину пропорционалан је количини електричног набоја који се налази унутар запремине те површине. Ако унутар те затворене површине нема електричног набоја (или је количина позитивног једнака количини негативног електричног набоја), укупни електрични ток кроз ту затворену површину је нула. То не значи да у тој запремини уопште нема електричног поља, већ само да укупни ток ишчезава. Дакле, ако нема електричног набоја у тох посматраној запремини, колико силница електричног поља улази кроз површину која описује запремину, толико силница негде и излази из те исте затворене површине.

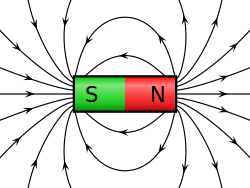
Друга Максвелова једначина слична је првој (у ситуацији у којој не постоји набој), али описује магнетно поље. Ова једначина изриче да не постоји „магнетни набој” (магнетни монопол), то јест не постоји извор магнетног поља, из којега би произлазио магнетни ток различит од нуле. У свакој тачки простора, количина силница магнетног поља која улази у ту тачку једнака је количини силница које излазе из те тачке, силнице магнетног поља немају извора (или понора). Стога укупни магнетни ток кроз затворену површину увек ишчезава. То вреди и за изворе магнетног поља, стога је сваки извор магнетног поља барем дипол.

Максвелове једначине у макроскопском медију (средству)

Максвелове једначине описују понашање електричног и магнетног поља свугде у простору, ако су познати сви извори, то јест набоји и струје. У опису макроскопских објеката такав приступ није могућ из два разлога. Прво, број наелектрисаних честица у атомима и нуклеарним језграма врло је велик. Други је разлог да са макроскопске тачке гледања, сви детаљи у понашању поља и набоја на атомским и молекуларним димензијама нису релевантни. Оно што је битно, то је просечна вредност поља и извора у запремини која је велика у поређењу са једним атомом или молекулом. Овакве просечне вредности називају се макроскопска поља и макроскопски извори. У овом случају Максвелове једначине попримају облик:

$\nabla \cdot \mathbf {D} ={\rho _{slob.}}$

$\nabla \cdot \mathbf {B} =0$

$\nabla \times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}=0$

$\nabla \times \mathbf {H} -{\frac {\partial \mathbf {D} }{\partial t}}={\mathbf {J} _{slob.}}$

где је:

$\mathbf {D} \$ - поље електричног помака,

$\mathbf {H} \$ - магнетизирајуће поље,

${\rho _{slob.}}\$ - густина слободног електричног набоја (укупна густина електричног набоја минус густина везаних електричних набоја),

${\mathbf {J} _{slob.}}\$ - густина слободне електричне струје (укупна густина електричне струје минус густина везаних електричних струја).

Величине $\mathbf {D} \$ i $\mathbf {H} \$ није једноставно одредити, јер је у њима садржана целокупна сложеност интеракције поља и средства (медија, то јест материјала у којем се поље налази). Могуће је да ове величине зависе од претходног стања средства (хистерезис), такође је могуће да су нелинеарне и просторно анизотропне. Ове једначине за поља у средству нису толико универзалне као почетно наведене једначине. Ипак, Ј. К. Максвел их је на сличан начин првобитно формулисао. Везе између $\mathbf {E} \$ i $\mathbf {D} \$ te između $\mathbf {B} \$ i $\mathbf {H} \$ зову се конститутивне релације.

У најједноставнијем случају претпоставља се, да су електрична и магнетска својства средства хомогена и изотропна, те да се поља не мењају интензивно у времену. У стварности то вреди за диелектричне и парамагнетске материјале. Тада спољашње електрично поље ствара поларизацију $\mathbf {P} \$, која је линеарно пропорционална електричном пољу, док магнетно поље ствара магнетизацију $\mathbf {M} \$ пропорционалну магнетном пољу, те вреди:

$\mathbf {P} \ =\chi _{e}\cdot \epsilon _{0}\cdot \mathbf {E}$

$\mathbf {M} \ =\chi _{m}\cdot \mathbf {H}$

Тада је:

$\mathbf {D} \ =\epsilon _{0}\cdot \mathbf {E} +\mathbf {P} =\epsilon _{0}\cdot (1+\chi _{e})\cdot \mathbf {E} =\epsilon \cdot \mathbf {E}$

$\mathbf {B} =\mu _{0}\cdot (\mathbf {H} +\mathbf {M} )=\mu _{0}\cdot (1+\chi _{m})\cdot \mathbf {H} =\mu \cdot \mathbf {H}$

Опис закона

Гаусов закон

Гаусов закон описује однос међу статичким електричним пољем и наелектрисања које ствара то поље.

Види још

• Лоренцова сила
• Био-Саваров закон
• Кулонов закон

Литература

• On Faraday's Lines of Force – 1855/56 Maxwell's first paper (Part 1 & 2) – Compiled by Blaze Labs Research (PDF)
• On Physical Lines of Force – 1861 Maxwell's 1861 paper describing magnetic lines of Force – Predecessor to 1873 Treatise
• James Clerk Maxwell, "A Dynamical Theory of the Electromagnetic Field", Philosophical Transactions of the Royal Society of London 155, 459–512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
  • A Dynamical Theory Of The Electromagnetic Field – 1865 Maxwell's 1865 paper describing his 20 Equations, link from Google Books.
• J. Clerk Maxwell (1873) A Treatise on Electricity and Magnetism
  • Maxwell, J.C., A Treatise on Electricity And Magnetism – Volume 1 – 1873 – Posner Memorial Collection – Carnegie Mellon University
  • Maxwell, J.C., A Treatise on Electricity And Magnetism – Volume 2 – 1873 – Posner Memorial Collection – Carnegie Mellon University
• Joseph Larmor (1897) "On a dynamical theory of the electric and luminiferous medium", Phil. Trans. Roy. Soc. 190, 205–300 (third and last in a series of papers with the same name).
• Hendrik Lorentz (1899) "Simplified theory of electrical and optical phenomena in moving systems", Proc. Acad. Science Amsterdam, I, 427–43.
• Hendrik Lorentz (1904) "Electromagnetic phenomena in a system moving with any velocity less than that of light", Proc. Acad. Science Amsterdam, IV, 669–78.
• Henri Poincaré (1900) "La théorie de Lorentz et le Principe de Réaction", Archives Néerlandaises, V, 253–78.
• Henri Poincaré (1902) La Science et l'Hypothèse
• Henri Poincaré (1905) "Sur la dynamique de l'électron", Comptes Rendus de l'Académie des Sciences, 140, 1504–8.
• Catt, Walton and Davidson. "The History of Displacement Current". Wireless World, March 1979. Архивирано на сајту Wayback Machine (6. мај 2008)
• Imaeda, K. (1995), "Biquaternionic formulation of Maxwell’s Equations and their solutions", Clifford Algebras and Spinor Structures (editors—Rafał Ablamowicz, Pertti Lounesto) Springer; . doi:10.1007/978-94-015-8422-7_16. 

Спољашње везе

• Hazewinkel Michiel, ур. (2001). „Maxwell equations”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104. 
• maxwells-equations.com — An intuitive tutorial of Maxwell's equations.
• Mathematical aspects of Maxwell's equation are discussed on the Dispersive PDE Wiki.
• Electromagnetism (ch. 11), B. Crowell, Fullerton College
• Lecture series: Relativity and electromagnetism, R. Fitzpatrick, University of Texas at Austin
• Electromagnetic waves from Maxwell's equations on Project PHYSNET.
• MIT Video Lecture Series (36 × 50 minute lectures) (in .mp4 format) – Electricity and Magnetism Taught by Professor Walter Lewin.
• -author= -
• Nature Milestones: Photons – Milestone 2 (1861) Maxwell's equations