Algoritam obrnutog brisanja

Algoritam obrnutog brisanja je algoritam u teoriji grafova koji se koristi za dobijanje minimalnog razapinjućeg stabla iz datog povezanog težinskog grafa . On se prvi put pojavio kod Kruskala 1956, ali to ne treba mešati sa algoritmom Kruskala koji se pominje u ovoj oblasti. Ukoliko graf nije povezan, ovaj algoritam će naći minimalno razapinjuće stablo, odvojeno za svaki deo grafa. Skup ovih minimalnih razapinjućih stabala se zove minimalna razapinjuća šuma, koja sadrži svaki čvor grafa.

Ovaj algoritam je pohlepni algoritam, bira najbolji izbor u svakom trenutku u zadatoj situaciji. To je suprotno od Kruskalovog algoritma, što je još jedan pohlepni algoritam koji pronalazi minimalno Razapinjuće stablo. Kruskalov algoritam počinje sa praznim grafom i dodaje grane, dok obrnuto brisanje počinje sa originalnom grafom i briše iz njega grane. Algoritam radi na sledeći način:

• Počinje sa grafom G, koji sadrži listu grana E.
• Ide do E po opadajućem redosledu težine grana.
• Za svaku granu, proverite da li će brisanje napraviti nepovezan graf.
• Izvršite brisanja koja ne dovode do dodatnih isključenja.

Pseudokod

 1  function ReverseDelete(edges[] E)
 2    sort E in decreasing order
 3    Define an index i ← 0
 4    while i < size(E)
 5       Define edge temp ← E[i]
 6	   delete E[i]
 7	   if temp.v1 is not connected to temp.v2
 8             E[i] ← temp
 9   	   i ← i + 1
 10   return edges[] E

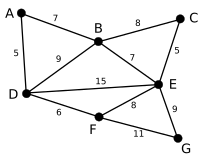
Gornji graf je skup grana E gde svaka grana ima težinu i povezuje čvorove v1 i v2.

Primer

U sledećem primeru zelene grane se procenjuju u algoritmu a crvene grane su izbrisane.

	Ovo je naš originalni graf. Brojevi na grani govore težinu grane.
	Algoritam će početi sa granom maksimalne težine, što je u ovo slučaju DE težine 15. Pošto brisanje grana DE ne uzrokuje raspadanje grafa, grana se briše.
	Sledeća najveća grana je FG , algoritam će proveriti da li brisanjem ove grane dolazi do raspada grafa. Pošto brisanje grane neće dovesti dotle, grana je tada obrisana.
	Sledeća najveća grana je BD, pa će algoritam proveriti ovu granu i izbrisati je.
	Sledeća grana je da proverite granu EG, koja neće biti izbrisana jer bi isključili čvor G iz grafa. Dakle, sledeća grana za brisanje je BC.
	Sledeća najveća grama je grana EF, tako će algoritam proveriti ovu granu i izbrisati je.
	Algoritam će onda tražiti preostale grane i neće naći drugu granu da obriše, pa ovo je konačni graf koji nam vraća algoritam.

Vreme izvršavanja

Za algoritam se može dokazati da radi u O (E log V (log log V)³) vremenu, gde jeE je broj grama i V je broj čvorova. Ova granica se dostiže na sledeći način:

• Sortiranje grana po težini pomoću poređenja u O ( E log E) vremenu
• E iteracije petlje
• Brisanje uO (1) vremenu
• Povezivanje proveriti u O(logV (log log V)³) vremenu Thorup 2000.

Isto tako, vreme rada može se smatrati O (E log E (log log E)³) jer najveći E može se V ². Zapamtite da logV ² = 2 * log V, pa 2 je multiplikativna konstanta koja će biti ignorisana u notaciji velikog O.