Bernulijeva jednačina

Venturijeva cev: pritisak u prvoj mernoj tački u cevi (1) je viši nego u drugoj (2), a brzina fluida „1” je niža u mernoj tački „2”, jer je poprečni presek u tački „1” veći nego u „2”.

Bernulijeva jednačina je jedna od osnovnih matematičkih definicija, u delu fizike, koja se zove dinamika fluida. Opisuje Bernulijev princip, odnosno definiše međusobnu vezu između pritiska ili potencijalne energije fluida i njegove brzine ili njegove kinetičke energije, u strujnoj cevi (strujnom polju). Bernulijev princip je dobio ime po dansko-švajcarskom naučniku Danijelu Bernuliju, koji je opisao ovaj princip u svojoj knjizi Hidrodinamica 1738. godine. Bernulijeva jednačina služi upravo za opisivanje ovog principa i izračunavanje parametara vezanih za protok fluida.

Postoji više oblika Bernulijeve jednačine koje opisuju razne vrste protoka fluida. Najjednostavniji oblik Bernulijeve jednačine se odnosi na slučaj kada se gustina fluida može uzeti kao nepromenljiva (kod tečnosti i kod zanemarivanja stišljivosti gasa na malim brzinama). Postoji i jednačina za protok fluida kada se gustina ne može uzeti kao konstantna. Kod većih brzina gasova, kada se mora uzimati u obzir njihova stišljivost, tada se uvodi u jednačinu Mahov broj, kao ekvivalent brzine. Bernulijeva jednačina se dodatno usložnjava ako se radi o viskoznom strujanju.

Bernulijev princip se može izvesti iz zakona o održanju energije. Naime, iz ovog zakona sledi da u mirnom toku fluida suma svih oblika mehaničkih energija, u celom strujnom toku, mora biti jednaka u svima tačkama toga polja. Drugim rečima, suma kinetičke i potencijalne energije mora biti međusobno jednaka u svima tačkama strujnog polja.

Čestice fluida su pod uticajem sopstvene težine i pritiska, kreću se između tačaka sa različitim statičkim pritiskom, od većeg prema manjem. Ako se fluid kreće horizontalno, kroz strujnu cev, brzina će se povećavati ako se ta razlika statičkog pritiska povećava između dve tačke, odnosno između dva preseka cevi. Brzina fluida se smanjuje ako se ta razlika statičkog pritiska smanjuje. Najveća brzina je tamo gde je pritisak najmanji, a najmanja je tamo gde je pritisak najveći.

Energija tečnosti

Geodetska visina je visina tečnosti koja se može spustiti i izvršiti rad, a jednaka je njenoj potencijalnoj energiji.

Toričelijev zakon isticanja.

Tečnosti mogu imati energiju u različitim oblicima.

Potencijalna energija tečnosti

Glavni članak: Potencijalna energija

Tečnost mase m (kg), koja se nalazi na nekoj visini z (m), merenoj od neke vodoravne ravni, ima potencijalnu energiju:

$E_{p}=m\cdot g\cdot z$

Naime sa te visine tečnost se može spustiti i izvršiti rad kolika je njena potencijalna energija. Visina z, na kojoj se tečnost nalazi, zove se geodetska visina. Ona se meri geodetskim instrumentom, totalnom stanicom ili teodolitom.

Energija pritiska tečnosti

Tečnost ima energiju i zbog hidrostatičkog pritiska p. Ako se priključi na izlaznu cev posude, u kojoj se nalazi tečnost, jedna uska cev. Tečnost će se u toj cevi dignuti na visinu h, koja odgovara hidrostatičkom pritisku, to jest:

$h={p \over \rho \cdot g}$

a energija pritiska ove tečnosti zapremine V jeste:

$m\cdot g\cdot h=\rho \cdot V\cdot g\cdot h=p\cdot V$

Visina na koju se tečnost podigne zbog hidrostatičkog pritiska zove se manometarska visina.

Kinetička energija tečnosti

Glavni članak: Kinetička energija

Zamislimo rezervoar u koji dotiče tačnost sa strane tako da uvek stoji na istom nivou. Na dnu rezervoara nalazi se otvor kroz koji tečnost ističe. Tečnost mase m (kg) na nekoj visini h ima potencijalnu energiju m ∙ g ∙ h. Kad tečnost ističe kroz otvor na dnu rezervoara, potencijalna se energija tečnosti pretvara u kinetičku energiju, pa mora biti:

$m\cdot g\cdot h={\frac {m\cdot v^{2}}{2}}$

gde je v brzina isticanja tečnosti. Iz ovog izraza proizlazi da je visina tečnosti, na koju bi se ona popela zbog kinetičke energije:

$h={\frac {v^{2}}{2\cdot g}}$

Ta visina, koja daje tečnosti brzinu v, zove se visina brzine i ona je merilo za kinetičku energiju tečnosti.

Objašnjenje Bernulijeve jednačine

Da bi se objasnila Bernulijeva jednačina, na levu posudu se dodaje vodoravna staklena cev koja se sužava i na sebi ima uspravne staklene cevi. Ako se začepi otvor na kraju cevi desno i napuni posuda vodom do visine h, voda će po zakonu o spojenim posudama stajati svuda jednako visoko do visine h. Kad se vodoravna cev desno otčepi, voda će početi da ističe i ona neće u svim cevčicama stajati jednako visoko, što znači da pritisci u tečnosti koja struji nisu na svim mestima jednaki. Vidi se da je pritisak na kraju cevi desno jednak nuli, a odavde prema unutrašnjosti uniformno raste, što pokazuje pravac koji spaja vrhove stubaca vode u okomitim cevčicama. Pritisak pada ravnomerno (proporcionalno) s dužinom cevi. Pad pritiska je smanjenje pritiska na jedinici dužine cevi. Prema tome zaključuje se da je strujanje tečnosti kroz dugačke cevi drugačije u pogledu pritiska, a i brzine, nego što to daje Toričelijev zakon isticanja. Pritisak koji tečnost ima u strujanju zove se hidrodinamički pritisak.

Šema Bernulijeve jednačine

Iz eksperimenta vidi se da pritisak u vodoravnoj cevi stalno opada, te da je hidrodinamički pritisak na svakom mestu manji od hidrostatičkog pritiska koji bi postojao kad mi voda mirovala. Ako je cev svuda istog preseka, to po principu kontinuiteta brzina mora biti svuda ista. Ovo je moguće samo stoga što su čestice vode terane stalnim pritiskom (to jest stalnom silom), jer bi inače trenje postepeno poništilo njihovu kinetičku energiju. Visina h₁ stuba vode u strujanju prestavlja visinu otpora, to jest onaj pritisak koji je potreban za svladavanje otpora duž cevi. Visina h₂ je visina brzine koja daje tečnosti brzinu u strujanju. Odatle se vidi da se hidrostatski pritisak h delimično troši na svladavanje otpora, a preostali deo daje tečnosti brzinu.

Po zakonu kontinuiteta kroz svaki presek cevi mora proći u jedinici vremena ista količina tečnosti.

Da bi se ustanovilo po kojem se zakonu vlada pritisak kod tečnosti u strujanju, može se razmatrati jedna nagnuta cev kojoj se presek prema kraju smanjuje. Budući da po zakonu kontinuiteta kroz svaki presek mora proći u jedinici vremena ista količina tečnosti, to će brzine u raznim presecima biti različite. Tako će u preseku I brzina biti v₁, u preseku II brzina v₂, a u preseku III brzina v₃. Ako se zanemari trenje (idealna tečnost), u svakoj tački strujnog mlaza mora, po zakonu o održanju energije, ukupna energija ostati uvek ista. Uzima se da kroz svaki presek u jedinici vremena prolazi m kilograma tečnosti.

U položaju I energija tečnosti sastoji se od 3 dela:

• od potencijalne energije, koja iznosi m ∙ g ∙ z₁, gde se visina z₁ meri od nivoa isticanja,
• od energije pritiska p₁ ∙ V,
• od kinetičke energije m ∙ v₁² / 2.

Prema tome vredi, u položaju I:

$E_{1}=m\cdot g\cdot z_{1}+p_{1}\cdot V+{\tfrac {1}{2}}\ \cdot m\cdot v_{1}^{2}$

u položaju II:

$E_{2}=m\cdot g\cdot z_{2}+p_{2}\cdot V+{\tfrac {1}{2}}\ \cdot m\cdot v_{2}^{2}$

u položaju III:

$E_{3}=m\cdot g\cdot z_{3}+p_{3}\cdot V+{\tfrac {1}{2}}\ \cdot m\cdot v_{3}^{2}$

Uz pretpostavku da nema trenja, po zakonu o održanju energije mora biti:

$E_{1}=E_{2}=E_{3}$

odnosno generalno vredeti:

$m\cdot g\cdot z+p\cdot V+{\tfrac {1}{2}}\ \cdot m\cdot v^{2}=\,{\text{константа}}\,$

Kondenzacija vidljiva na gornjoj površini krila vazduhoplova Airbus A340 uzrokovana padom temperature koja nastaje zbog pada pritiska.

To je Bernulijev zakon strujanja, koji glasi: Zbir pritisne, potencijalne i kinetičke energije pri stacionarnom strujanju idealne tečnosti je konstantna veličina.

Ako se podeli gornju jednačinu sa V, dobija se:

${\frac {m}{V}}\ \cdot g\cdot z+p+{\tfrac {1}{2}}\ \cdot {\frac {m}{V}}\ \cdot v^{2}=\,{\text{константа}}\,$

budući da za gustinu tečnosti vredi:

$\rho ={m \over V}$

dobija se:

${\tfrac {1}{2}}\,\cdot \rho \,\cdot v^{2}\,+\,\rho \,\cdot g\,\cdot z\,+\,p\,=\,{\text{константа}}\,$

što je Bernulijeva jednačina koja se odnosi na jedinicu mase idealne tečnosti. Svi članovi u ovom izrazu imaju jedinicu pritiska. Veličina ρ ∙ v² / 2 zove se hidrodinamički pritisak, jer njegova vrednost zavisi od brzine tečnosti.

Ako se podeli gornji izraz sa ρ ∙ g dobija se:

${\frac {p}{\rho \cdot g}}\ +z+{\frac {v^{2}}{2\cdot g}}\ =\,{\text{константа}}\,$

Ovo je oblik Bernulijeve jednačine koji se odnosi na jedinicu težine idealne tečnosti. Njeni članovi imaju dimenziju dužine. Naime p / ρ g = h i prestavlja manometarsku visinu, odnosno energiju jedinice težine tečnosti. Naime, energija tečnosti težine G je:

$G\cdot h={\frac {G\cdot p}{\rho \cdot g}}\$

Ako je G = 1, onda je energija p / ρ ∙ g. Član z je geodetska visina i prestavlja potencijalnu energiju težine tečnosti. Naime, tečnost težine G ima na visini z energiju G ∙ z. Ako je G = 1, onda je potencijalna energija jednaka z. Član v2 / 2 ∙ g je visina brzine, te ima takođe dimenziju dužine, to jest brojno daje kinetičku energiju jedinice težine tečnosti. Naime, tečnost težine G, to jest mase m = G / g i brzine v ima kinetičku energiju G / g v² / 2, a tečnosti težine G = 1 ima kinetičku energiju v² / 2 ∙ g.

Prema tome, Bernulijeva jednačina se može izraziti i ovako: Pri stacionarnom strujanju idealne tečnosti je zbir geodetske visine, manometarske visine i visine brzine u svakoj tački duž strujanja stalna veličina.

Označimo li se ukupni pritisak u tečnosti koja struji sa p_o, može se napisati i ovako:

${\tfrac {1}{2}}\,\cdot \rho \,\cdot v^{2}\,+\,\rho \,\cdot g\,\cdot z\,+\,p\,=p_{0}$

Protiče li tečnost kroz vodoravnu cev, onda je z = 0, pa je:

$p_{0}=\,p\,+{\tfrac {1}{2}}\,\cdot \rho \,\cdot v^{2}\,$

Iz toga proizlazi da je zbir hidrostatičkog i hidrodinamičkog pritiska idealne tečnosti na svim mestima vodoravnog cevovoda konstantan. Iz prethodnog izraza proizlazi takođe važan zaključak koji daje odnos između pritiska p i brzine v u svakom preseku. Naime, po zakonu kontinuiteta proizlazi da je u većem preseku neke cevi brzina mala, a iz Bernulijevog zakona strujanja izlazi da se u tom slučaju pritisak p mora povećati kako bi ukupan pritisak ostao isti. Iz toga se vidi da je kod strujanja tečnosti brzina u većem preseku mala, a pritisak velik, dok je u malom preseku brzina velika, a pritisak mali. Sniženje pritiska pare ili gasova kod prolaza kroz uske otvore zove se prigušivanje ili prigušenje. Bernulijev zakon vrijedi i za gasove. Kod strujanja gasova razlikuju se aerodinamički i aerostatički pritisak.

Osnovne i izvedene merne jedinice koje se koriste kod Bernulijeve jednačine

ρ = gustina - $(kg/m^{3})$

S = presek predstavlja površinu poprečnog preseka - $(m^{2})$.

P = statički pritisak - (Pa)

v = brzina - (m/s)

m = masa tečnosti - (kg)

R = mehanički rad - (J)

V = zapremina mase tečnosti - $(m^{3})$

Bernulijeva jednačina koristi SI sistem jedinica.

• $\ z$ = geodetska visina odnosno visina težišta poprečnog preseka u odnosu na neku vodoravnu ravan u $\ (m)$
• $\ p \over \rho g$ = pijezometarska ili pritisna visina odnosno visina pijezometarskog pritiska koju pokazuje visina stuba tečnosti u pijezometarskoj cevi u $\ (m)$
• $\ {v^{2} \over 2g}$ = brzinska visina u $\ (m)$, a brzina $\ v$ predstavlja brzinu koju bi telo imalo kada bi bilo u slobodnom padu.
• Ukupan zbir energija daje Bernulijevu jednačinu

Ulaskom u uži deo cevi, preseka $S_{2}$ i statičkog pritiska $p_{2}$ tečnost dobije veću brzinu $v_{2}$. Masa tečnosti m ima u širem delu cevi kinetičku energiju:

${\frac {m\cdot v_{1}^{2}}{2}}$

a kad uđe u uži deo kinetičku energiju:

${\frac {m\cdot v_{2}^{2}}{2}}$

Povećanje kinetičke energije posledica je mehaničkog rada R koji je nastao radi razlike pritisaka ($p_{1}-p_{2}$) $s_{1}$ pri kretanju mase m tečnosti iz šireg dela cevi u uži na putu ΔS:

R = ($p_{1}-p_{2}$) $s_{1}$ ΔS

R = ($p_{1}-p_{2}$) V , gde je V zapremina mase tečnosti.

Taj je rad jednak povećanju kinetičke energije:

($p_{1}-p_{2}$) V = ${\frac {m\cdot v_{2}^{2}}{2}}$ - ${\frac {m\cdot v_{1}^{2}}{2}}$

Deljenjem gornje jednakosti sa zapreminom, znajući da je gustina ρ = ${\frac {m}{V}}$ dobija se Bernulijeva jednačina:

$p_{1}$ + ${\frac {\rho \cdot v_{1}^{2}}{2}}$ = $p_{2}$ + ${\frac {\rho \cdot v_{2}^{2}}{2}}$ = $p_{3}$ + ${\frac {\rho \cdot v_{3}^{2}}{2}}$ = konstanta.

Izrazi ${\frac {\rho \cdot v_{1}^{2}}{2}}$, $p_{2}$ + ${\frac {\rho \cdot v_{2}^{2}}{2}}$ i $p_{3}$ + ${\frac {\rho \cdot v_{3}^{2}}{2}}$ prikazuju pritisak koji je nastao usled strujanja tečnosti i zove se dinamički pritisak.

Oblik Bernulijeve jednačine za idealnu tečnost

Osnovne pretpostavke pod kojima vredi ova jednačina su:

1. Tečnost je idealna - nestišljiva tečnost, linija energije je konstantna duž preseka
2. Stacionarno strujanje

$\ z_{1}+{p_{1} \over \rho g}+{v_{1}^{2} \over 2g}=z_{2}+{p_{2} \over \rho g}+{v_{2}^{2} \over 2g}=H$

$\ H$ predstavlja hidrodinamički pritisak ili ukupnu specifičnu energiju u $\ (m)$.

Izvod Bernulieve jednačine preko zakona održanja količine kretanja

Bernulijeva jednačina je prvi put izvedena 1738. godine primenom zakona održanja količine kretanja.

Osnovne pretpostavke pod kojima vredi ovaj izvod su:

1. fiktivna cev ili proračun za konačni element neke cevi,
2. Stacionarno strujanje ili postupno promenjivo strujanje.

Izvod Bernulieve jednačine preko Ojlerovog integrala

Ojlerove diferencijalne jednačine kretanja tečnosti - implicitni oblik

$\ {\frac {1}{\rho }}{\frac {\delta p}{\delta x}}=X-{\frac {du}{dt}}$ ... ... ...(1E)

$\ {\frac {1}{\rho }}{\frac {\delta p}{\delta y}}=Y-{\frac {dv}{dt}}$ ... ... ...(2E)

$\ {\frac {1}{\rho }}{\frac {\delta p}{\delta z}}=Z-{\frac {dW}{dt}}$ ... ... ...(3E)

$\ \rho =konst$ - nema opšteg rešenja jer su prisutne 4 nepoznate. Rešenje je moguće samo ako definiše pretpostavka koja će eliminisati suvišnu nepoznatu.

Osnovna pretpostavka: postoji stacionarno strujanje

matematičke transformacije - (1E) se množi sa dx, (2E) se množi sa dy, (3E) se množi sa dz i sabiraju se dobijene jednačine.

$\ {\frac {1}{\rho }}({\frac {\delta p}{\delta x}}dx+{\frac {\delta p}{\delta y}}dy+{\frac {\delta p}{\delta z}}dz)=Xdx+Ydy+Zdz-(du\overbrace {\frac {dx}{dt}} ^{u}+dv\overbrace {\frac {dy}{dt}} ^{v}+dw\overbrace {{\frac {dz}{dt}})} ^{w}$

pa se dobija jednačina:

$\ 0=Xdx+Ydy+Zdz-{\frac {1}{\rho }}\delta p-(udu+vdv+wdw)$

ona se može derivisati

$\ udu={\frac {1}{2}}du^{2}$

$\ vdv={\frac {1}{2}}dv^{2}$

$\ wdw={\frac {1}{2}}dw^{2}$

pri čemu poprima ovaj oblik

$\ 0=Xdx+Ydy+Zdz-{\frac {\delta p}{\rho }}-{\frac {1}{2}}d(u^{2}+v^{2}+w^{2})$

$\ 0=Xdx+Ydy+Zdz-{\frac {\delta p}{\rho }}-{\frac {1}{2}}d(W^{2})$

ako postoji strujna cev u kojoj deluje samo gravitacija u normalnom koordinatnom sistemu. Može se pojednostaviti ovako;

$\ X=0,Y=0,Z=-g$

$\ -gdz-{\frac {\delta p}{\rho }}-{\frac {1}{2}}d(W^{2})=0...operacije/\int /:-g$

I konačno Ojlerov integral koji predstavlja izvod Bernulieve jednačine:

$\ z+{\frac {p}{\rho g}}+{\frac {W^{2}}{2g}}=konstanta$

Oblik Bernulijeve jednačine za realnu tečnost

$\ z_{1}+{p_{1} \over \rho g}+{\alpha _{1}v_{1}^{2} \over 2g}=z_{2}+{p_{2} \over \rho g}+{\alpha _{2}v_{2}^{2} \over 2g}+\Delta H$

$\ \Delta H$ je deo specifične energije utrošen na svladavanje hidrodinamičkih otpora strujanju tečnosti. Izražava se u $\ (m)$.

Koriolisov koeficijent

Ili koeficijent kinetičke energije $\ \alpha _{1,2}$. On pokazuje odnos stvarne kinetičke energije mase fluida koji protiče poprečnim presekom u jedinici vremena i kinetičke energije određene iz uslova da su brzine u svim tačkama preseka jednake (srednja brzina). Koeficijent kinetičke energije je bezdimenzionalna jedinica.

Koeficijent kinetičke energije najčešće ima sledeće vrednosti:

• kod strujanja u cevima $\alpha =1,0$
• kod strujanja u otvorenim vodotokovima $\alpha =1,1$
• vrednost $\alpha$ se može izračunati formulom:

$\ \alpha ={\frac {\int _{A}v^{3}dA}{v_{sr}^{3}A}}$ - uz uzlov da je $\alpha \geq 1$

Protok nestišljivih fluida

Dejstvo sila na delić fluida, u strujnom polju.

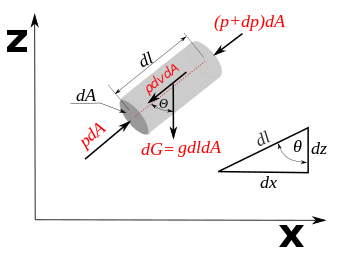
U slučaju većine tečnosti, i gasova sa malim mahovim brojem, gustina fluida se može smatrati konstantnom (odatle ‘’nestišljivih”), bez obzira na varijacije u pritisku.

U ovom slučaju Bernulijeva jednačina ima oblik:

${v^{2} \over 2}+gz+{p \over \rho }={\text{const}}$

gde je:

$v\,$ je Brzina protoka u nekoj tački toka,

$g\,$ je gravitaciono ubrzanje,

$z\,$ je visina po z-osi(pozitivan deo z-ose je usmeren prema gore, dakle suprotno od smera delovanja gravitacije)

$p\,$ je pritisak, i

$\rho \,$ je gustina fluida u svim tačkama fluida.

Važne napomene:

• fluid mora biti nestišljiv — uprkos promenjivom pritisku, gustina mora ostati ista da bi jednačina važila;
• ovaj oblik Bernulijeve jednačine važi za slučaj kada su viskozne sile zanemarljive.

Ako se gornja jednačina pomnoži sa gustinom dobija se sledeća jednačina:

Protok vazduha u mernoj venturi cevi. Kinetička energija je povećavana na račun pada statičkog pritiska fluida, što prikazuje razlika visina vodenog stuba u
U cevi.

${\tfrac {1}{2}}\,\rho \,v^{2}\,+\,\rho \,g\,z\,+\,p\,=\,{\text{const}}\,$

ili:

$q\,+\,\rho \,g\,h\,=\,p_{0}\,+\,\rho \,g\,z\,=\,{\text{const}},$

gde je:

$q\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}$ dinamički pritisak.

U pojednostavljenom posmatranju (pogotovo ako je fluid gas), pritisak je usled težine stuba fluida u posmatranom malom deliću, zanemarljivo je mali. Na osnovu toga je realno usvojiti: ρgz = 0. Tada Bernulijeva jednačina dobija jednostavniji oblik:

$\ p+{\frac {\rho \,\ v^{2}}{2}}=\,{\text{constant}}\,\quad \longmapsto \quad \ p+\ q=\,{\text{const}}\,$

Zbir statičkog i dinamičkog pritiska u svim tačkama strujne cevi je konstantan broj. Ova jednačina se još naziva i jednačinom o održanju energije.

Protok stišljivih fluida

Gornje jednačine važe za nestišljive fluide, međutim moguće je, koristeći fundamentalne fizičke zakone, doći do jednačina koji su slične njima ali su primenjive i na stišljive (barotoropne) fluide. Postoji mnogo oblika Bernulijeve jednačine i sve su one analogne osnovnoj Bernulijevoj jednačini i oslanjaju se na fundamentalne zakone poput Njutnovih zakona i prvog zakona termodinamike.

Jedna od najčešće korišćenih jednačina za stišljive fluide je:

${\frac {v^{2}}{2}}+\int _{p_{1}}^{p}{\frac {d{\tilde {p}}}{\rho ({\tilde {p}})}}\ +\Psi ={\text{const}}$

gde je:

p — pritisak,

ρ — gustina tečnosti,

v — brzina protoka i

Ψ — gravitacioni potencijal.

Vidi još

• Termodinamika
• Aerodinamika
• Dinamika fluida

Spoljašnje veze

• O kretanju fluida