Paralelni transport na sferi Kristofelovi simboli u diferencijalnoj geometriji predstavljaju koeficijente koji opisuju paralelni transport u krivolinijskim koordinatnim sistemima. Dobili su ime po nemačkom matematičaru Elvinu Brunu Kristofelu . Kristofelovi simboli prve vrste označavaju se sa
[
μ
ν
,
κ
]
=
Γ
μ
ν
κ
,
{\displaystyle [\mu \nu ,\kappa ]=\Gamma _{\mu \nu \kappa },}
{
σ
μ
ν
}
=
Γ
μ
ν
σ
{\displaystyle {\begin{Bmatrix}\sigma \\\mu \nu \end{Bmatrix}}=\Gamma _{\;\mu \nu }^{\sigma }}
Slika 1. Kada u krivolinijskom sistemu oduzimamo dva vektora pored uobičajene razlike dva vektora u pravougaonom sistemu imamo i dodatnu razliku zbog paralelnoga transporta jednoga vektora do drugoga. Neka u
x
i
{\displaystyle x^{i}}
A
i
,
{\displaystyle A^{i},}
x
i
+
d
x
i
{\displaystyle x^{i}+dx^{i}}
A
i
+
d
A
i
.
{\displaystyle A^{i}+dA^{i}.}
A
i
{\displaystyle A^{i}}
x
i
+
d
x
i
{\displaystyle x^{i}+dx^{i}}
δ
A
i
.
{\displaystyle \delta A^{i}.}
D
A
i
=
d
A
i
−
δ
A
i
{\displaystyle DA^{i}=dA^{i}-\delta A^{i}}
Paralelni transport zavisan je od Kristofelovih simbola :
δ
A
i
=
−
Γ
i
k
ℓ
A
k
d
x
l
.
{\displaystyle \delta A^{i}=-\Gamma ^{i}{}_{k\ell }A^{k}dx^{l}.}
Tu se koristi Ajnštajnova konvencija da se sumira po indeksima koji se pojavljauju više puta.
Slika 2. Uzmimo polarni koordinatni sistem u kome se tačka nalazi na udaljenosti
r
{\displaystyle {r}}
φ
.
{\displaystyle \varphi .}
A
{\displaystyle {\boldsymbol {A}}}
(
a
,
α
)
{\displaystyle (a,\,\alpha )}
a
{\displaystyle a}
α
{\displaystyle \alpha }
A
{\displaystyle {\boldsymbol {A}}}
|
A
|
2
=
a
2
+
r
2
α
2
{\displaystyle |A|^{2}=a^{2}+r^{2}\alpha ^{2}}
a na drugom je:
a
2
+
(
r
+
d
r
)
2
(
α
+
d
α
)
2
=
a
2
+
r
2
α
2
,
{\displaystyle a^{2}+(r+{\rm {d}}r)^{2}(\alpha +{\rm {d}}\alpha )^{2}=a^{2}+r^{2}\alpha ^{2},}
pa se dobija:
d
α
=
−
1
r
α
d
r
.
{\displaystyle {\rm {d}}\alpha =-{\frac {1}{r}}\,\alpha \,{\rm {d}}r.}
Paralelan transport duž luka [ uredi | uredi izvor ] Tokom translacije duž luka menjaju se obe koordinate, pa sa slike 2 vidimo da je:
α
=
A
r
sin
λ
{\displaystyle \alpha ={\frac {A}{r}}\sin \lambda }
a
=
A
cos
λ
{\displaystyle a=A\cos \lambda }
d
λ
=
−
d
φ
{\displaystyle {\rm {d}}\lambda =-{\rm {d}}\varphi }
d
α
=
−
1
r
a
d
φ
.
{\displaystyle {\rm {d}}\alpha =-{\frac {1}{r}}\,a\,{\rm {d}}\varphi .}
Osim toga pošto je
a
=
A
cos
λ
{\displaystyle a=A\cos \lambda }
d
λ
=
−
d
φ
{\displaystyle {\rm {d}}\lambda =-{\rm {d}}\varphi }
A
sin
λ
=
r
α
{\displaystyle A\sin \lambda =r\alpha }
d
a
=
−
(
−
r
)
α
d
φ
.
{\displaystyle {\rm {d}}a=-(-r)\,\alpha \,{\rm {d}}\varphi .}
Označimo li:
x
1
=
r
{\displaystyle x^{1}=r}
x
2
=
φ
{\displaystyle x^{2}=\varphi }
A
1
=
a
{\displaystyle {A^{1}=a}}
A
2
=
α
{\displaystyle A^{2}=\alpha }
δ
A
i
=
−
Γ
i
k
ℓ
A
k
d
x
l
.
{\displaystyle \delta A^{i}=-\Gamma ^{i}{}_{k\ell }A^{k}dx^{l}.}
mogu dobiti Kristofelovi simboli kao:
Γ
22
1
=
−
r
{\displaystyle {\Gamma _{22}^{1}=-r}}
Γ
12
2
=
Γ
21
2
=
1
/
r
{\displaystyle \Gamma _{12}^{2}=\Gamma _{21}^{2}=1/r}
Kristofelovi simboli prve i druge vrste [ uredi | uredi izvor ] Kristofelovi simboli prve i druge vrste povezani su sledećom relacijom:
Γ
c
a
b
=
g
c
d
Γ
d
a
b
,
{\displaystyle \Gamma _{cab}=g_{cd}\Gamma ^{d}{}_{ab}\,,}
Kristofelovi simboli povezani su sa metričkim tenzorom. Ako znamo metrički tenzor za neki krivolinijski sistem tada se Kristofelovi simboli druge vrste mogu potpuno predstaviti preko odgovarajućega matričkoga tenzora:
Γ
i
k
ℓ
=
1
2
g
i
m
(
∂
g
m
k
∂
x
ℓ
+
∂
g
m
ℓ
∂
x
k
−
∂
g
k
ℓ
∂
x
m
)
=
1
2
g
i
m
(
g
m
k
,
ℓ
+
g
m
ℓ
,
k
−
g
k
ℓ
,
m
)
,
{\displaystyle \Gamma ^{i}{}_{k\ell }={\frac {1}{2}}g^{im}\left({\frac {\partial g_{mk}}{\partial x^{\ell }}}+{\frac {\partial g_{m\ell }}{\partial x^{k}}}-{\frac {\partial g_{k\ell }}{\partial x^{m}}}\right)={1 \over 2}g^{im}(g_{mk,\ell }+g_{m\ell ,k}-g_{k\ell ,m}),\ }
a tu je
g
i
j
{\displaystyle g^{ij}\ }
g
i
j
{\displaystyle g_{ij}\ }
g
i
j
g
j
k
=
δ
k
i
{\displaystyle g^{ij}g_{jk}=\delta _{k}^{i}\ }
Γ
n
,
i
j
{\displaystyle \Gamma _{n,ij}^{}}
Γ
n
,
i
j
=
g
k
n
Γ
i
j
k
=
1
2
(
∂
g
i
n
∂
x
j
+
∂
g
j
n
∂
x
i
−
∂
g
i
j
∂
x
n
)
{\displaystyle \Gamma _{n,ij}=g_{kn}\Gamma _{ij}^{k}={\tfrac {1}{2}}\left({\frac {\partial g_{in}}{\partial x^{j}}}+{\frac {\partial g_{jn}}{\partial x^{i}}}-{\frac {\partial g_{ij}}{\partial x^{n}}}\right)}
Kristofelovi simboli su simetrični po donjim indeksima;
Γ
i
j
k
=
Γ
i
k
j
.
{\displaystyle \Gamma ^{i}{}_{jk}=\Gamma ^{i}{}_{kj}.}
S druge strane kovarijantan izvod metričkoga tenzora može se prikazati preko Kristofelovih simbola:
∇
ℓ
g
i
k
=
∂
g
i
k
∂
x
ℓ
−
g
m
k
Γ
m
i
ℓ
−
g
i
m
Γ
m
k
ℓ
=
0.
{\displaystyle \nabla _{\ell }g_{ik}={\frac {\partial g_{ik}}{\partial x^{\ell }}}-g_{mk}\Gamma ^{m}{}_{i\ell }-g_{im}\Gamma ^{m}{}_{k\ell }=0.\ }
Za sferni koordinatni sistem komponente metričkoga tenzora su
g
θ
θ
=
r
2
{\displaystyle g_{\theta \theta }=r^{2}}
g
ϕ
ϕ
=
r
2
sin
2
θ
{\displaystyle g_{\phi \phi }=r^{2}\sin ^{2}\theta }
g
θ
θ
,
r
=
2
r
{\displaystyle g_{\theta \theta ,r}=2r}
g
ϕ
ϕ
,
r
=
2
r
sin
2
θ
{\displaystyle g_{\phi \phi ,r}=2r\sin ^{2}\theta }
g
ϕ
ϕ
,
θ
=
2
r
2
cos
θ
sin
θ
{\displaystyle g_{\phi \phi ,\theta }=2r^{2}\cos \theta \sin \theta }
Γ
θ
θ
r
=
−
r
Γ
ϕ
ϕ
r
=
−
r
sin
2
θ
Γ
r
θ
θ
=
Γ
θ
r
θ
=
r
−
1
Γ
ϕ
ϕ
θ
=
−
cos
θ
sin
θ
Γ
r
ϕ
ϕ
=
Γ
ϕ
r
ϕ
=
r
−
1
Γ
ϕ
θ
ϕ
=
Γ
θ
ϕ
ϕ
=
cot
θ
{\displaystyle {\begin{aligned}\Gamma _{\theta \theta }^{r}&=-r\\\Gamma _{\phi \phi }^{r}&=-r\sin ^{2}\theta \\\Gamma _{r\theta }^{\theta }=\Gamma _{\theta r}^{\theta }&=r^{-1}\\\Gamma _{\phi \phi }^{\theta }&=-\cos \theta \sin \theta \\\Gamma _{r\phi }^{\phi }=\Gamma _{\phi r}^{\phi }&=r^{-1}\\\Gamma _{\phi \theta }^{\phi }=\Gamma _{\theta \phi }^{\phi }&=\cot \theta \end{aligned}}}
Za cilindrični koordinatni sistem simboli su:
Γ
ϕ
ϕ
r
=
−
r
Γ
r
ϕ
ϕ
=
Γ
ϕ
r
ϕ
=
1
r
{\displaystyle {\begin{aligned}\Gamma _{\phi \phi }^{r}&=-r\\\Gamma _{r\phi }^{\phi }=\Gamma _{\phi r}^{\phi }&={\frac {1}{r}}\end{aligned}}}
Preko Kristofelovih simbola prikazuje se kovarijantan izvod tenzora :
Kovarijantni izvod tenzorskoga polja
A
i
k
{\displaystyle A^{ik}\ }
∇
ℓ
A
i
k
=
∂
A
i
k
∂
x
ℓ
+
Γ
i
m
ℓ
A
m
k
+
Γ
k
m
ℓ
A
i
m
,
{\displaystyle \nabla _{\ell }A^{ik}={\frac {\partial A^{ik}}{\partial x^{\ell }}}+\Gamma ^{i}{}_{m\ell }A^{mk}+\Gamma ^{k}{}_{m\ell }A^{im},\ }
tj.
A
i
k
;
ℓ
=
A
i
k
,
ℓ
+
A
m
k
Γ
i
m
ℓ
+
A
i
m
Γ
k
m
ℓ
.
{\displaystyle A^{ik}{}_{;\ell }=A^{ik}{}_{,\ell }+A^{mk}\Gamma ^{i}{}_{m\ell }+A^{im}\Gamma ^{k}{}_{m\ell }.\ }
Za mešano tenzorsko polje imamo:
A
i
k
;
ℓ
=
A
i
k
,
ℓ
+
A
m
k
Γ
i
m
ℓ
−
A
i
m
Γ
m
k
ℓ
,
{\displaystyle A^{i}{}_{k;\ell }=A^{i}{}_{k,\ell }+A^{m}{}_{k}\Gamma ^{i}{}_{m\ell }-A^{i}{}_{m}\Gamma ^{m}{}_{k\ell },\ }
a za tenzorsko polje polje tipa (0,2) kovarijantan izvod je:
A
i
k
;
ℓ
=
A
i
k
,
ℓ
−
A
m
k
Γ
m
i
ℓ
−
A
i
m
Γ
m
k
ℓ
.
{\displaystyle A_{ik;\ell }=A_{ik,\ell }-A_{mk}\Gamma ^{m}{}_{i\ell }-A_{im}\Gamma ^{m}{}_{k\ell }.\ }
Kovarijantni izvod za neki tenzor tipa (n, m) je:
∇
k
v
j
1
⋯
j
m
i
1
⋯
i
n
=
∂
∂
x
k
v
j
1
⋯
j
m
i
1
⋯
i
n
+
∑
α
=
1
n
Γ
k
ℓ
i
α
v
j
1
⋯
j
m
i
1
⋯
i
α
−
1
ℓ
i
α
+
1
⋯
i
n
−
∑
α
=
1
m
Γ
k
i
α
ℓ
v
j
1
⋯
j
α
−
1
ℓ
j
α
+
1
⋯
j
m
i
1
⋯
i
n
{\displaystyle \nabla _{k}v_{j_{1}\cdots j_{m}}^{i_{1}\cdots i_{n}}={\frac {\partial }{\partial x^{k}}}v_{j_{1}\cdots j_{m}}^{i_{1}\cdots i_{n}}+\sum _{\alpha =1}^{n}\Gamma _{k\ell }^{i_{\alpha }}\ v_{j_{1}\cdots j_{m}}^{i_{1}\cdots i_{\alpha -1}\ \ell \ i_{\alpha +1}\cdots i_{n}}-\sum _{\alpha =1}^{m}\Gamma _{ki_{\alpha }}^{\ell }\ v_{j_{1}\cdots j_{\alpha -1}\ \ell \ j_{\alpha +1}\cdots j_{m}}^{i_{1}\cdots i_{n}}}
Koristi se Ajnštajnova konvencija da se sumira po indeksima koji se pojavljauju više puta.
Kontrakcijom Kristofelovih simbola odnosno sumacijom po indeksu, koji se ponavlja dobija se:
Γ
i
k
i
=
1
2
g
i
m
∂
g
i
m
∂
x
k
=
1
2
g
∂
g
∂
x
k
=
∂
log
|
g
|
∂
x
k
{\displaystyle \Gamma ^{i}{}_{ki}={\frac {1}{2}}g^{im}{\frac {\partial g_{im}}{\partial x^{k}}}={\frac {1}{2g}}{\frac {\partial g}{\partial x^{k}}}={\frac {\partial \log {\sqrt {|g|}}}{\partial x^{k}}}\ }
i
g
k
ℓ
Γ
i
k
ℓ
=
−
1
|
g
|
∂
(
|
g
|
g
i
k
)
∂
x
k
{\displaystyle g^{k\ell }\Gamma ^{i}{}_{k\ell }={\frac {-1}{\sqrt {|g|}}}\;{\frac {\partial \left({\sqrt {|g|}}\,g^{ik}\right)}{\partial x^{k}}}}
Tu je |g | determinanta od
g
i
j
{\displaystyle g_{ij}\ }
g
i
j
{\displaystyle g^{ij}\ }
g
i
j
g
j
k
=
δ
k
i
{\displaystyle g^{ij}g_{jk}=\delta _{k}^{i}\ }
Pri transformaciji jednoga sistema
(
x
1
,
.
.
.
,
x
n
)
{\displaystyle (x^{1},...,x^{n})\ }
(
y
1
,
.
.
.
,
y
n
)
{\displaystyle (y^{1},...,y^{n})\ }
∂
∂
y
i
=
∂
x
k
∂
y
i
∂
∂
x
k
{\displaystyle {\frac {\partial }{\partial y^{i}}}={\frac {\partial x^{k}}{\partial y^{i}}}{\frac {\partial }{\partial x^{k}}}\ }
pa se dobija formula transformacije Kristofelovih simbola:
Γ
k
i
j
¯
=
∂
x
p
∂
y
i
∂
x
q
∂
y
j
Γ
r
p
q
∂
y
k
∂
x
r
+
∂
y
k
∂
x
m
∂
2
x
m
∂
y
i
∂
y
j
{\displaystyle {\overline {\Gamma ^{k}{}_{ij}}}={\frac {\partial x^{p}}{\partial y^{i}}}\,{\frac {\partial x^{q}}{\partial y^{j}}}\,\Gamma ^{r}{}_{pq}\,{\frac {\partial y^{k}}{\partial x^{r}}}+{\frac {\partial y^{k}}{\partial x^{m}}}\,{\frac {\partial ^{2}x^{m}}{\partial y^{i}\partial y^{j}}}\ }
Kristofelov simbol Kobayashi, Shoshichi and Nomizu, Katsumi (1996 (New edition)). Foundations of Differential Geometry, Vol. 1. Wiley Interscience. ISBN 978-0-471-15733-5 .
Sternberg, Shlomo (1964). Lectures on Differential Geometry. Prentice-Hall 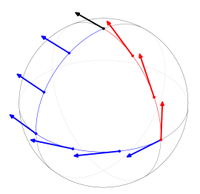



![{\displaystyle [\mu \nu ,\kappa ]=\Gamma _{\mu \nu \kappa },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39ed7210dffe16f7ad91c7166bc2f4224e9bb49e)

























































