Površina

Ukupna površina ova tri oblika je približno 15,57 kvadrata.

Površina je geometrijski pojam koji označava meru veličine geometrijske slike u euklidskom dvodimenzionalnom prostoru. Tačka i linija nemaju površinu, odnosno njihova površina je nula. Sa druge strane ravan ima beskonačnu površinu. Površina je takođe i deo tela u prostoru koji je izložen spoljašnjosti. Merenjem površina su se bavili još stari Egipćani, ali su ga do nivoa nauke podigli tek stari Heleni. Kod njih se površina neke geometrijske slike izračunavala tako što se nizom transformacija pretvara u kvadrat iste površine. Potom se izmere stranice kvadrata i lako izračuna površina. Od tih dana je izračunavanje površine dobilo drugi naziv: kvadratura.

Površina je količina koja opisuje u kojoj je meri dvodimenzionalna figura ili oblik, ili planarne lamine, u ravni. Površina je njen analogni pojam na dvodimenzionalnoj površi trodimenzionalnog oblika. Površina može biti shvaćena kao količina materijala sa datom debljinom koja bi bila potrebna da obuče model oblika, ili količina boje potrebne da prekrije površ sa uniformnim nanosom. To je dvodimenzionalni analog dužine krive (jednodimenzionalni koncept) ili zapremine čvrstog tela (trodimenzionalni koncept).

U SI sistemu, standardna jedinica površine je kvadratni metar (piše se kao m²), što je površina kvadrata čije su stranice duge po jedan metar. Oblik sa površinom od tri kvadratna metra bi imao istu površinu kao i tri takva kvadrata. U matematici, jedinica kvadrata je definisana da ima površinu od jedan, i površinu od bilo kojeg oblika ili površi je bezdimenzioni realni broj.

Postoji nekoliko dobro poznatih formula za površine manjih oblika kao što su trouglovi, pravougaonici i krugovi. Koristeći ove formule, površina svakog poligona može se naći deljenjem poligona u trouglove. Za oblike sa zakrivljenim granicama, kalkulus se često koristi da se izračuna površina. Doista, problem određivanja površine ravnih figura bio je veća motivacija za istorijski razvoj kalkulusa (matematička analiza).

Za čvrsti oblik kao što je sfera, konus ili cilindar, površina njihovih površi naziva se površina površi. formule za površine jednostavnih oblika bile su računate u doba drevnih Grka, ali računanje površine komplikovanijih oblika obično zahteva multivarijabilni kalkulus.

Površina igra važnu ulogu u modernoj matematici. U dodatku sa očiglednom važnošću u geometriji i kalkulusu, površina je vezana za definiciju determinanti u linearnoj algebri, te je osnovna osobina površi u diferencijalnoj geometriji. U analizi, površina podskupa ravni je definisana korištenjem mere Lebega, Generalno, površina u višoj matematici vidi se kao specijalan slučaj zapremine za dvodimenzionalne regije.

Površina može biti definisana kroz upotrebu aksioma, definišući je kao funkciju kolekcije određenih ravnih figura u skup realnih brojeva. Može biti dokazano da takva funkcija postoji.

Formalna definicija

Pojam „površine” su definiše aksiomima. Površina može biti definisana kao funkcija iz kolekcije M specijalne vrste ravnih figura (nazvani merljivi skupovi) ka skupu realnih brojeva koji zadovoljavaju sledeće osobine:

• Za sve S u M, a(S) ≥ 0.
• Ako su S i T u M tada su i S ∪ T i S ∩ T, i takođe a(S∪T) = a(S) + a(T) − a(S∩T).
• Ako su S i T u M sa S ⊆ T tada je T − S u M i a(T−S) = a(T) − a(S).
• Ako je skup S u M i S je kongruentno sa T tada T je takođe u M i a(S) = a(T).
• Svaki pravougaonik R je u M. Ako pravougaonik ima dužinu h i širinu k tada je a(R) = hk.
• Neka Q bude skup zatvoren između dve step regije S i T. Step regija je formirana od ograničene unije susjednih pravougaonika koji se nalaze na istoj bazi, npr. S ⊆ Q ⊆ T. Ako postoji unikatan broj c takav da je a(S) ≤ c ≤ a(T) za sve takve step regije S i T, tada je a(Q) = c.

Može biti dokazano da takva površinska funkcija zaista postoji.

Istorija

Površina kruga

U 5. veku p. n. e., Hipokrat sa Hiosa je bio prvi da pokaže da je površina diska (regiona obuhvaćenog krugom) proporcionalna kvadratu njegovog prečnika, kao deo njegove kvadrature Hipokritovog meseca, ali nije identifikovao konstantu proporcionalnosti. Eudoks je isto tako u 5. veku p. n. e., utvrdio da je površina diska proporcionalna kvadratu njegovog prečnika.

Knjiga I Euklidovih Elemenata se bavi jednakošću oblasti između dvodimenzionalnih figura. Matematičar Arhimed je koristio oruđa Euklidove geometrije da pokaže da je oblast unutar kruga jednaka površini pravougaonog trougla čija baza ima dužinu obima kruga i čija visina je jednaka poluprečniku kruga, u svojoj knjizi Merenje kruga. (Obim je 2πr, i površina trougla je polovina baze puta visina, iz čega sledi da je površina diska πr².) Arhimed je aproksimirao vrednost parametra π (i stoga je površina kruga jediničnog poluprečnika) putem njegovog metoda udvostručavanja, u kome je upisivao regularni trougao u krug, beležio njegovu površinu, i zatim udvostručavao broj strana da bi dobio regularni heksagon, nakon toga je ponavljao udvostručavanje broja strana čime je površina poligona postajala sve bliža površini kruga (i isto je radio sa opisanim poligonima).

Švajcarski naučnik Johan Hajnrih Lambert je 1761. godine dokazao da je π, odnos površine kruga i kvadrata njegovog poluprečnika, i da je jednaka iracionalnom broju, što znači da nije jednaka količniku bilo koja dva cela broja. Godine 1794. je francuskim matematičar Adrijen-Mari Ležandr dokazao da je π² iracionalna vrednost; time je takođe dokazano da je π iracionalno. Godine 1882, nemački matematičar Ferdinand fon Lindeman dokazao da je π transcendentna vrednost (da nije rešenje bilo koje polinomne jednačine sa racionalnim koeficijentima), čime je potvrdio pretpostavku Ležandra i Ojlera.

Površina trougla

Heron (ili Hero) od Aleksandrije utvrdio je Heronovu formulu za površinu trougla izraženu odnosom njegovih strana, i dokaz se može naći u njegovoj knjizi, Metrika, koju je napisao oko 60. godine. Po nekim izvorima Arhimed je znao tu formulu par vekova ranije, i pošto je Metrika kolekcija matematičkog znanja dostupnog u antičkom svetu, moguće je da ta formula predatira reference date u tom radu.

Godine 499. Arijabhata, veliki matematičar-astronom iz klasičnog doba indijske matematike i indijske astronomije, izrazio je površinu trougla kao jednu polovinu baze pomnoženu visinom u svom radu Aryabhatiya (sekcija 2.6).

Kinezi su nezavisno od Grka otkrili Formulu ekvivalentnu Heronovoj. To je bilo objavljeno 1247. godine u radu Šušu Điuzhang („Matematička rasprava u devet sekcija”), autora Ćin Đušao.

Kvadrilateralna površina

U 7. veku, Bramagupta je razvio formulu, koja je u današnje vreme poznata kao Formula Bramagupte, za površinu tetivnog četvorougla (četvorougla upisanog u krug) u smislu njegovih strana. Godine 1842. nemački matematičari Karl Anton Bretšnajder i Karl Georg Hristijan Štaudt nezavisno su izveli formulu, poznatu kao Bretšnajderova formula, za površinu bilo kog četvorougaonika.

Opšta površina poligona

Rene Dekartov razvoj Kartezijanski koordinata u 17. veku omogućio je Gausu da razvije geodetske formule za površinu bilo kog poligona sa poznatim lokacijama temenom u 19. veku.

Površine utvrđene korišćenjem računa

Razvoj integralnog računa u kasnom 17. veku pružio je oruđa koja se mogu koristiti za izračunavanje komplikovanijih površina, kao što je površina elipse i površinske oblasti raznih zakrivljenih trodimenzionih objekata.

Formule za površinu

Formule poligona

Glavni članak: Mnogougao § Površina i centroid

Za (jednostavni) poligon koji ne preseca samog sebe, kartezijanske koordinate $(x_{i},y_{i})$ (i=0, 1, ..., n-1) čijih n temena je poznato, površina je data geodetskom formulom:

$A={\frac {1}{2}}|\sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i})|,$

gde kad je i=n-1, onda je i+1 izraženo kao modulo n i stoga se odnosi na 0.

Pravougaonici

Površina ovog pravougaonika je lw.

Najosnovnija formula površine je formula za površinu pravougaonika. Ako je dat pravougaonik sa dužinom l i širinom w, formula za površinu je:

A = lw (pravougaonik).

Površina pravougaonika je dužina pomnožena širinom. Kao specijalni slučaj, kad je l = w u slučaju kvadrata, površina kvadrata sa dužinom strane s je data formulom:

A = s² (kvadrat).

Formula za površinu pravougaonika sledi direktno iz osnovnih svojstava površine, i ponekad se uzima kao definicija ili aksiom. S druge strane, da je geometrija razvijena pre aritmetike, ova formula bi se mogla koristiti za definisanje množenja realnih brojeva.

Figure jednake površine.

Disekcija, paralelogrami i trouglovi

Glavni članci: Trougao § Računanje površine trougla i Paralelogram § Formula površine

Većina drugih jednostavnih formula za površinu sledi iz metoda disekcije. Time je obuhvaćeno deljenje oblika u komade, pri čemu je suma površina komada jednaka površini originalnog oblika.

Na primer, bilo koji paralelogram se može podeliti u trapezoid i pravougaoni trougao, kao što je prikazano na slici levo. Ako se trougao pomeri na drugu stranu trapezoida, onda je rezultirajuća figura pravougaonik. Iz ovoga sledi da je površina paralelograma jednaka površini pravougaonika:

A = bh (paralelogram).

Dva jednaka trougla.

Međutim, isti paralelogram se isto tako može preseći duž dijagonale u dva podudarna trougla, kao što je prikazano na slici s desne strane. Površina svakog trougla je polovina površine paralelograma:

$A={\frac {1}{2}}bh$ (trougao).

Slični argumenti mogu se koristiti za pronalaženje formule za površinu trapezoida kao i komplikovanijih poligona.

Površina zakrivljenih oblika

Krugovi

Krug se može podeliti u sektore koi se mogu rearanžirati da formiraju približni paralelogram.

Glavni članak: Površina kruga

Formula za površinu kruga (preciznije površina obuhvaćena krugom ili površina diska) bazirana je na sličnom metodu. Polazeći od poluprečnika kruga r, moguće je podeliti krug u sektore, kao što je prikazano na slici desno. Svaki sektor je približno trougaon po obliku, i sektori se mogu aranžirati tako da formiraju približni paralelogram. Visina paralelograma je r, a širina je polovina obima kruga, ili πr. Stoga je totalna površina kruga πr²:

A = πr² (krug).

Mada je disekcija koja se koristi u ovoj formuli samo približna, greška postaje sve manja i manja kako se krug deli u sve manje i manje sektore. Limit površine aproksimiranog paralelograma je precizno πr², što je površina kruga.

Ovaj argument je zapravo jednostavna primena ideje infinitezimalnog računa. U antička vremena, metod iscrpljivanja je korišten na sličan način za nalaženje površine kruga, i taj metod se sad smatra prekurzorom integralnog računa. Koristeći moderne metode, površina kruga se može izračunati koristeći određeni integral:

$A\;=\;2\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx\;=\;\pi r^{2}.$

Elipse

Glavni članak: Elipsa § Površina

Formula za površinu obuhvaćenu elipsom je srodna formuli za krug; za elipsu sa velikom i malom poluosom x i y formula je:

$A=\pi xy.$

Površina tela

Glavni članak: Površina tela

Arhimed je pokazao da je površina sfere jednaka sa tačno četiri površine kruga istog poluprečnika, i da je zapremina sfere tačno 2/3 zapremine cilindra iste visine i poluprečnika.

Većina osnovnih formula za površinu tela se može dobiti presecanjem i poravnavanjem površina. Na primer, ako se bočna površina cilindra (ili bilo koje prizme) uzdužno preseče, površina se može poravnati u pravougaonik. Slično tome, ako se preseče jedna strana kupe, bočna površina se može poravnati u sektor kruga, i rezultirajuća površina se može izračunati.

Formulu za površinu sfere je teže izvesti: pošto sfera ima nenultu Gausova zakrivljenost, ona se ne može poravnati. Formulu za površinu sfere je prvi izveo Arhimed u svom radu O sferi i cilindru. Formula je:

A = 4πr² (sfera),

gde je r radijus sfere. Kao sa formulom površine kruga, svako izvođenje ove formule nasledno koristi metode slične metodima kalkulusa.

Opšte formule

Površine dvodimenzionalnih figura

• Trougao: ${\tfrac {1}{2}}Bh$ (gde je B bilo koja strana, i h je rastojanje od linije na kojoj B leži do drugog temena trougla). Ova formula se može koristiti ako je visina h poznata. Ako su poznate dužine tri strane onda se može koristiti Heronova formula: ${\sqrt {s(s-a)(s-b)(s-c)}}$ gde su a, b, c strane trougla, i $s={\tfrac {1}{2}}(a+b+c)$ je polovina njegovog obima. Ako su jedan ugao i dve strane date, površina je ${\tfrac {1}{2}}ab\sin(C)$ gde je C dati ugao i a i b su strane. Ako je trougao prikazan na koordinatnoj ravni, može se koristiti matrica koja se pojednostavljuje apsolutnom vrednošću izraza ${\tfrac {1}{2}}(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3})$. Ova formula je poznata kao formula pertle i to je jedan jednostavan način izračunavanja površine trougla zamenom koordinata tri tačke (x₁, y₁), (x₂, y₂), i (x₃, y₃). Formula pertle se isto tako može koristiti za nalaženje površine drugih poligona kad su njihova temena poznata. Još jedan pristup nalaženju površine koordinatnog trougla je putem kalkulusa.
• jednostavni poligon konstruisan na mreži ravnomerno razmaknutih tačaka (tj., tačaka sa celobrojnim koordinatama) takvoj da su sva temena poligona tačke na mreži: $i+{\frac {b}{2}}-1$, gde je i broj tačaka mreže unutar poligona i b je broj graničnih tačaka. Ovaj rezultat je poznat kao Pikova teorema.

Površina u računu

Integracija se može poistovetiti sa merenjem površine ispod krive, definisane sa f(x), između dve tačke (ovde a i b).

Površina između dva grafa se može izračunati kao razlika integrala dve funkcije

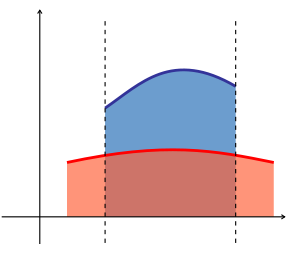
• Površina između krive s pozitivnim vrednostima i horizontalne ose, merene između dve vrednosti a i b (b je definisana kao veća od ove dve vrednosti) na horizontalnoj osi, je dato integralom od a do b funkcije koja predstavlja krivu:

$A=\int _{a}^{b}f(x)\,dx.$

• Površina između grafova dve funkcije je jednaka integralu jedne funkcije, f(x), minus integral druge funkcije, g(x):

$A=\int _{a}^{b}(f(x)-g(x))\,dx,$ gde je $f(x)$ kriva sa većim y-vrednostima.

• Površina ograničena funkcijom r = r(θ) izraženom u polarnim koordinatama je:

$A={1 \over 2}\int r^{2}\,d\theta .$

• Oblast obuhvaćena parametarskom krivom ${\vec {u}}(t)=(x(t),y(t))$ sa krajnjim tačkama ${\vec {u}}(t_{0})={\vec {u}}(t_{1})$ je data linijskim integralom:

$\oint _{t_{0}}^{t_{1}}x{\dot {y}}\,dt=-\oint _{t_{0}}^{t_{1}}y{\dot {x}}\,dt={1 \over 2}\oint _{t_{0}}^{t_{1}}(x{\dot {y}}-y{\dot {x}})\,dt$

(pogledajte Grinovu teoremu) ili z-komponentu od

${1 \over 2}\oint _{t_{0}}^{t_{1}}{\vec {u}}\times {\dot {\vec {u}}}\,dt.$

Ograničena površina između dve kvadratne funkcije

Da bi se našla ograničena površina između dve kvadratne funkcije, potrebno je oduzeti jednu od druge

$f(x)-g(x)=ax^{2}+bx+c=a(x-\alpha )(x-\beta )$

gde je f(x) kvadratna gornja granica i g(x) je kvadratna donja granica. Diskriminanta f(x)-g(x) se definiše kao

$\Delta =b^{2}-4ac.$

Pojednostavljujući integralnu formulu između grafova dve funkcije (kao što je dato u gornjoj sekciji) i koristeći Vijetove formule, dobija se

$A={\frac {\Delta {\sqrt {\Delta }}}{6a^{2}}}={\frac {a}{6}}(\beta -\alpha )^{3},\qquad a\neq 0.$

Ovo ostaje validno ako je jedna od funkcija linearna.

Površina trodimenzionalnih figura

• Kupa: $\pi r\left(r+{\sqrt {r^{2}+h^{2}}}\right)$, gde je r poluprečnik kružne osnove, i h je visina. Ovo se isto tako može napisati kao $\pi r^{2}+\pi rl$ ili $\pi r(r+l)\,\!$ gde je r poluprečnik i l je visina nagiba kupe. $\pi r^{2}$ je baza površine, dok je $\pi rl$ lateralna površina kupe.
• kocka: $6s^{2}$, gde je s dužina ivice.
• cilindar: $2\pi r(r+h)$, gde je r poluprečnik osnove i h je visina. 2$\pi$r se takođe može napisati kao $\pi$ d, gde je d dikametar.
• prizma: 2B + Ph, gde je B površina osnove, P je obim baze, i h je visina prizme.
• piramida: $B+{\frac {PL}{2}}$, gde je B površina osnove, P je obim osnove, i L je dužina nagiba.
• pravougaona prizma: $2(\ell w+\ell h+wh)$, gde je $\ell$ dužina, w je širina, i h je visina.

Opšta formula za površinu

Opšta formula za površinu grafa neprekidno diferencijabilne funkcije $z=f(x,y),$ gde je $(x,y)\in D\subset \mathbb {R} ^{2}$ i $D$ je region u xy-ravni sa glatkim granicama:

$A=\iint _{D}{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}\,dx\,dy.$

Još opštija formula za površinu grafa parametarske površine u vektorskom obliku $\mathbf {r} =\mathbf {r} (u,v),$ gde je $\mathbf {r}$ neprekidno diferencijabilna vektorska funkcija $(u,v)\in D\subset \mathbb {R} ^{2}$ je:

$A=\iint _{D}\left|{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}\right|\,du\,dv.$

Osnovne formule

Formule za račun površina:
Slika	Formula	Objašnjenje
Pravougaonik	$l\cdot w\,$	$l$ i $w$ su dužina i širina pravougaonika.
Trougao	${\frac {1}{2}}b\cdot h\,$	$b$ i $h$ su osnovica i visina.
Krug	$\pi \cdot r^{2}\,$	$r$ je poluprečnik.
Elipsa	$\pi \cdot a\cdot b\,$	$a$ i $b$ su velika i mala poluosa.
Sfera	$4\pi r^{2}\,$, ili $\pi d^{2}\,$	$r$ je poluprečnik, a $d$ je prečnik.
Trapez	${\frac {1}{2}}(a+b)h\,$	$a$ i $b$ su paralelne strane, a $h$ je rastojanje među paralelama.
Valjak	$2\pi r(h+r)\,$	$r$ i $h$ su poluprečnik i visina.
Omotač valjka	$2\pi rh\,$	$r$ i $h$ su poluprečnik i visina.
Kupa	$\pi r(l+r)\,$	$r$ i $l$ su poluprečnik i dužina stranice kupe.
Omotač kupe	$\pi rl\,$	$r$ and $l$ su poluprečnik i dužina stranice kupe.
Kružni isečak	${\frac {1}{2}}r^{2}\theta \,$	$r$ i $\theta$ su poluprečnik i ugao (u radijanima).

Merne jedinice

Prema SI sistemu jedinica mera, koji je i kod nas na snazi, osnovna merna jedinica površine je kvadratni metar (m²), a mogu se koristiti i iz nje izvedene veličine:

• 1 dm² = 0.01 m² = 10^-2m² (retko se koristi)
• 1 cm² = 0.0001 m² = 10^-4m² (retko se koristi)
• 1 mm² = 0.000001 m² = 10^-6m² (koristi se za merenje površine preseka žice u elektrotehnici)

Za merenje površine terena koriste se veće mere:

• 1 ar = 100 m² = 10²m²
• 1 ha = 10 000 m² = 10⁴m² (jedan hektar)
• 1 km² = 1 000 000 m² = 10⁶m² (jedan kvadratni kilometar)

Vidi još

• Površ

Literatura

• Eves, Howard (1990). An Introduction to the History of Mathematics (6th izd.). Saunders. str. 121. ISBN 978-0-03-029558-4. 
• Arndt, Jörg; Haene l, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Pristupljeno 5. 6. 2013.  English translation by Catriona and David Lischka.</ref> Godine 1794. je francuskim matematičar Adrijen-Mari Ležandr dokazao da je π² iracionalna vrednost; time je takođe dokazano da je π iracionalno.<ref>Eves, Howard (1990). An Introduction to the History of Mathematics (6th izd.). Saunders. str. 121. ISBN 978-0-03-029558-4. 
• Stewart, James (2003). Single variable calculus early transcendentals. (5th. izd.). Toronto ON: Brook/Cole. str. 3. ISBN 978-0-534-39330-4. „However, by indirect reasoning, Eudoxus (fifth century B.C.) used exhaustion to prove the familiar formula for the area of a circle: $A=\pi r^{2}.$” 
• Heath, Thomas L. (2003). A Manual of Greek Mathematics. Courier Dover Publications. str. 121—132. ISBN 978-0-486-43231-1. 
• Moise, Edwin (1963). Elementary Geometry from an Advanced Standpoint. Addison-Wesley Pub. Co. Pristupljeno 15. 7. 2012. 
• Rudin, Walter (1966). Real and Complex Analysis. McGraw-Hill. ISBN 978-0-07-100276-9. 
• Boyer, Carl B. (1959). A History of the Calculus and Its Conceptual Development. Dover. ISBN 978-0-486-60509-8. 

Spoljašnje veze

• Surface Area Video at Thinkwell