Prizma (geometrijska figura)
| Skup uniformnih n-gonalnih prizmi | |
|---|---|
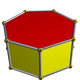
 Primer uniformne heksagonalne prizme | |
| Type | Uniformna u smislu polupravilnog poliedra |
| Strane | 2 n-gonalna regularna poligona n kvadrata |
| Ivice | 3n |
| Temena | 2n |
| Konfiguracija temena | 4.4.n |
| Šlaflijev simbol | {n}×{} [1] t{2, n} |
| Konvejova notacija | Pn |
| Koksterov dijagram | |
| Grupa simetrije | Dnh, [n,2], (*n22), red 4n |
| Grupa rotacije | Dn, [n,2]+, (n22), red 2n |
| Dualni poliedar | Konveksna dualna-uniformna n-gonalna bipiramida |
| Svojstva | konveksna, regularna poligonska lica, temeno-tranzitivne, translirane osnove, strane ⊥ baze |
| Mreža | |
 | |
Prizma je geometrijski poliedar ograničen sa dve paralelne podudarne osnove (osnova može biti bilo koji mnogougao) koje su povezane paralelogramima (bočnim stranama). U zavisnosti od mnogougla u osnovi, prizma može biti trougaona, četvorougaona, petougaona itd. Svi poprečni preseci paralelni sa osnovama su translacije osnova. Prizme su nazvane po svojim osnovama, npr. prizma sa petougaonom osnovom naziva se petougaona prizma. Prizme su podklasa prizmatoida.
Kao i mnogi osnovni geometrijski termini, reč prizma (od grčki πρίσμα (prizma) sa značenjem „nešto testerisano”) prvi put je upotrebljena u Euklidovim elementima. Euklid je definisao termin u Knjizi XI kao „čvrsta figura koju ograničavaju dve suprotne, jednake i paralelne ravni, dok su ostale paralelogrami“. Međutim, ova definicija je kritikovana jer nije dovoljno konkretna u odnosu na prirodu osnova, što je izazvalo zabunu među kasnijim piscima geometrije.[2][3]
Desna prizma, jednolična prizma[uredi | uredi izvor]

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|

|

|

|
Desna prizma[uredi | uredi izvor]
Prava prizma je prizma u kojoj su spojne ivice i lica okomite na osnovne površine.[4] Ovo važi ako su sve spojne površine pravougaone.
Dual prave n-prizme je prava n-bipiramida.
Desna prizma (sa pravougaonim stranicama) sa pravilnim n-ugaonim osnovama ima Šaflijev simbol { }×{n}. Ona se približava cilindričnom čvrstom telu kako se n približava beskonačnosti.
Posebni slučajevi[uredi | uredi izvor]
- Prava pravougaona prizma (sa pravougaonom osnovom) se takođe naziva kuboid, ili neformalno pravougaona kutija. Pravougaona prizma ima Šaflijev simbol { }×{ }×{ }.
- Prava kvadratna prizma (sa kvadratnom osnovom) se takođe naziva kvadratni kuboid ili neformalno kvadratna kutija.
Napomena: neki tekstovi mogu primeniti termin pravougaona prizma ili kvadratna prizma i na pravu pravougaonu prizmu i na pravu kvadratnu prizmu.
Uniformna prizma[uredi | uredi izvor]
Uniformna prizma ili polupravilna prizma je prava prizma sa pravilnim osnovama i kvadratnim stranicama, pošto su takve prizme u skupu uniformnih poliedara.
Uniformna n-ugaona prizma ima Šaflijev simbol t{2,n}.
Desne prizme sa pravilnim osnovama i jednakim dužinama ivica formiraju jedan od dva beskonačna niza polupravilnih poliedara, dok su druge serije antiprizme.
Podela[uredi | uredi izvor]
- Prave i kose prizme
- Trostrane, četvorostrane, petostrane ...
- Pravilne i nepravilne
Pravilna prizma je ona prizma koja u osnovi ima pravilan mnogougao (trougao, četvorougao, petougao itd.)
Delovi prizme[uredi | uredi izvor]
- Prava
- Osnova (Basis)
- Bočna strana
- Osnovna ivica
Površina prizme[uredi | uredi izvor]
Površina prizme je zbir površina svih strana prizme. Najjednostavnije je izračunati površinu bočnih strana -M- prizme i saberemo sa dve osnove.
gde je B površina osnove, h visina, a P obim osnove.
Površina prave prizme čija je osnova pravilan n-strani mnogougao sa dužinom stranice s i visinom h je prema tome:
Zapremina prizme[uredi | uredi izvor]
Zapreminu prizme izračunavamo tako što površinu osnove prizme pomnožimo visinom prizme.
gde je B površina osnove, a h visina. Zapremina prizme čija je osnova n-strani pravilan mnogougao sa dužinom stranice s je prema tome:
Šlegelovi dijagrami[uredi | uredi izvor]
 P3 |
 P4 |
 P5 |
 P6 |
 P7 |
 P8 |
Simetrija[uredi | uredi izvor]
Grupa simetrije prave n-strane prizme sa pravilnom osnovom je Dnh reda 4n, osim u slučaju kocke, koja ima veću grupu simetrije Oh reda 48, koja ima tri verzije D4h kao podgrupe. Rotaciona grupa je Dn reda 2n, osim u slučaju kocke, koja ima veću grupu simetrije O reda 24, koja ima tri verzije D4 kao podgrupe.
Grupa simetrije Dnh sadrži inverziju ako je n parno.
Hozoedri i diedri takođe poseduju simetriju diedra, a n-ugaona prizma se može konstruisati geometrijskim skraćenjem n-ugaonog hozoedra, kao i kroz kantelaciju ili proširenje n-ugaonog diedra.
Skraćena prizma[uredi | uredi izvor]
Skraćena prizma je prizma sa neparalelnim gornjim i donjim stranama.[5]
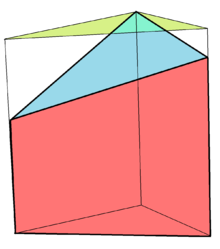
Uvrnuta prizma[uredi | uredi izvor]
Uvrnuta prizma je nekonveksni poliedar konstruisan od uniformne n-prizme sa svakom bočnom pločom podeljenom na polovinu kvadratne dijagonale, uvrtanjem vrha, obično za π/n radijana (180/n stepeni) u istom pravcu, što dovodi do konkavnih stranica.[6]<ref>„Pictures of Twisted Prisms”.
Uvrnuta prizma se ne može secirati na tetraedre bez dodavanja novih vrhova. Najmanji slučaj: trouglasti oblik, naziva se Šenhartov poliedar.
n-ugaona uvrnuta prizma je topološki identična n-ugaonoj uniformnoj antiprizmi, ali ima polovinu grupe simetrije: Dn, [n,2]+, reda 2n. Može se posmatrati kao nekonveksna antiprizma, sa tetraedrima uklonjenim između parova trouglova.
| 3-gonal | 4-gonal | 12-gonal | |
|---|---|---|---|
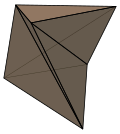 Šenhartov poliedar |
 Uvrnuta kvadratna prizma |
 Kvadratna antiprizma |
 Uvrnuta dodekagonalna antiprizma |
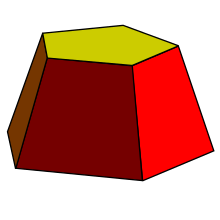
Frustum[uredi | uredi izvor]
Frustum je konstrukcija slična prizmi, sa trapeznim bočnim stranama i različitim velikim gornjim i donjim poligonima.
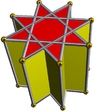
Zvezdana prizma[uredi | uredi izvor]
Zvezdana prizma je nekonveksni poliedar konstruisan od dve identične površine zvezdastog poligona na vrhu i dnu, paralelne i pomerene rastojanjem i povezane pravougaonim površinama. Uniformna zvezdana prizma će imati Šlaflijev simbol {p/q} × { }, sa p pravougaonikom i 2 {p/q} lica. Topološki je identična p-gonalnoj prizmi.
| { }×{ }180×{ } | ta{3}×{ } | {5/2}×{ } | {7/2}×{ } | {7/3}×{ } | {8/3}×{ } | |
|---|---|---|---|---|---|---|
| D2h, red 8 | D3h, red 12 | D5h, red 20 | D7h, red 28 | D8h, red 32 | ||

|

|

|

|

|

|
|
Ukrštena prizma[uredi | uredi izvor]
Ukrštena prizma je nekonveksni poliedar konstruisan od prizme, gde su vrhovi jedne osnove obrnuti oko centra ove osnove (ili rotirani za 180°). Ovo transformiše bočne pravougaone površine u ukrštene pravougaonike. Za pravilnu poligonsku osnovu, izgled je n-gonalni peščani časovnik. Sve kose ivice prolaze kroz jedan centar tela. Napomena: nijedan vrh nije u centru ovog tela. Ukrštena prizma je topološki identična n-ugaonoj prizmi.
| { }×{ }180×{ }180 | ta{3}×{ }180 | {3}×{ }180 | {4}×{ }180 | {5}×{ }180 | {5/2}×{ }180 | {6}×{ }180 | |
|---|---|---|---|---|---|---|---|
| D2h, red 8 | D3d, red 12 | D4h, red 16 | D5d, red 20 | D6d, red 24 | |||

|

|

|

|

|

|

|

|
Toroidna prizma[uredi | uredi izvor]
Toroidna prizma je nekonveksni poliedar poput ukrštene prizme, ali bez donje i gornje osnovne površine, i sa jednostavnim pravougaonim bočnim stranama koje zatvaraju poliedar. Ovo se može uraditi samo za jednostrane osnovne poligone. To su topološki tolozi, sa Ojlerovom karakteristikom za nulu. Topološka poliedarska mreža može biti isečena iz dva reda kvadratnih pločica (sa konfiguracijom temena 4.4.4.4): traka od n kvadrata, od kojih je svaki pričvršćen za ukršteni pravougaonik. n-ugaona toroidna prizma ima 2n vrhova, 2n lica: n kvadrata i n ukrštenih pravougaonika i 4n ivica. Topološki je samodualna.
| D4h, red 16 | D6h, red 24 |
| v=8, e=16, f=8 | v=12, e=24, f=12 |

|

|
Prizmatični politop[uredi | uredi izvor]
Prizmatični politop je višedimenzionalna generalizacija prizme. n-dimenzionalni prizmatični politop je konstruisan od dva (n − 1)-dimenzionalna politopa, prevedena u sledeću dimenziju.
Prizmatični n-politopni elementi se udvostručuju od (n − 1)-politopskih elemenata i zatim kreiraju nove elemente od sledećeg nižeg elementa.
Uzmimo n-politop sa fi i-stranim elementima (i = 0, ..., n). Njegova (n + 1)-politopna prizma će imati 2fi + fi−1 i-stranih elemenata. (Sa f−1 = 0, fn = 1.)
Po dimenziji:
- Uzmite mnogougao sa n vrhova, n ivica. Njegova prizma ima 2n temena, 3n ivica i 2 + n lica.
- Uzmite poliedar sa v vrhovima, e ivica i f površina. Njegova prizma ima 2v temena, 2e + v ivice, 2f + e lica i 2 + f ćelije.
- Uzmite polihoron sa v vrhovima, e ivica, f površina i c ćelija. Njegova prizma ima 2v temena, 2e + v ivice, 2f + e lica, 2c + f ćelija i 2 + c hiperćelije.
Ujednačeni prizmatični politop[uredi | uredi izvor]
Pravilan n-politop predstavljen Šlaflijevim simbolom {p, q, ..., t} može formirati uniforman prizmatični (n + 1)-politop predstavljen kartezijanskim proizvodom dva Šlaflijeva simbola: {p, q, ..., t}×{}.
Po dimenziji:
- 0-politopna prizma je segment linije, predstavljen praznim Šlaflijevim simbolom {}.
- 1-politopna prizma je pravougaonik, napravljen od 2 prevedena segmenta. Predstavlja se kao proizvod Šaflijevog simbola {}×{}. Ako je kvadratna, simetrija se može smanjiti: {}×{} = {4}.
- Poligonalna prizma je 3-dimenzionalna prizma napravljena od dva prevedena poligona povezana pravougaonicima. Pravilan mnogougao {p} može da konstruiše uniformnu n-ugaonu prizmu predstavljenu proizvodom {p}×{}. Ako je p = 4, sa kvadratnom simetrijom, postaje kocka: {4}×{} = {4, 3}.
 Primer: Pentagonalna prizma, {5}×{}, dva paralelna petougla povezana sa 5 pravougaonih stranica.
Primer: Pentagonalna prizma, {5}×{}, dva paralelna petougla povezana sa 5 pravougaonih stranica.
- Poliedarska prizma je 4-dimenzionalna prizma napravljena od dva prevedena poliedra povezana ćelijama 3-dimenzionalne prizme. Pravilan poliedar {p, q} može konstruisati uniformnu polihorijsku prizmu, predstavljenu proizvodom {p, q}×{}. Ako je poliedar kocka, a stranice kocke, on postaje teserakt: {4, 3}×{} = {4, 3, 3}.
 Primer: Dodekaedarska prizma, {5, 3}×{}, dva paralelna dodekaedra povezana sa 12 petougaonih stranica prizme.
Primer: Dodekaedarska prizma, {5, 3}×{}, dva paralelna dodekaedra povezana sa 12 petougaonih stranica prizme.
Prizmatični politopi višeg reda takođe postoje kao kartezijanski proizvodi bilo koja dva politopa. Dimenzija proizvoda politopa je proizvod dimenzija njegovih elemenata. Prvi primeri ovih postoje u 4-dimenzionalnom prostoru; nazivaju se duoprizmi kao proizvod dva poligona. Regularni duopizmi su predstavljeni kao {p}×{q}.
Galerija[uredi | uredi izvor]
-
Prava trostrana prizma
-
Kosa nepravila prizma
Reference[uredi | uredi izvor]
- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3b
- ^ Malton, Thomas (1774). A Royal Road to Geometry: Or, an Easy and Familiar Introduction to the Mathematics. ... By Thomas Malton. ... author, and sold. str. 360—.
- ^ Elliot, James (1845). Key to the Complete Treatise on Practical Geometry and Mensuration: Containing Full Demonstrations of the Rules ... Longman, Brown, Green, and Longmans. str. 3—.
- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, pp. 28
- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, pp. 81
- ^ Geometry handbookŽauthor=Catherine A. Gorini. The facts on file. 2003. str. 172. ISBN 0-8160-4875-4.
Literatura[uredi | uredi izvor]
- Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
- Ljiljana Petruševski - Poliedri
- Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
- Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ur.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. str. 43—70. ISBN 978-94-010-4398-4.
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Arhivirano na sajtu Wayback Machine (3. август 2016))
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8.
- Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067.
- Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678
- Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7
- Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093
 . doi:10.1007/s00373-002-0503-y. Arhivirano iz originala 2015-07-21. g.
. doi:10.1007/s00373-002-0503-y. Arhivirano iz originala 2015-07-21. g. - Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. str. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6.
- Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), str. 80—86, doi:10.1145/800061.808735
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd izd.), Oxford: Clarendon Press, MR 0124167.
- Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049.
- Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ur.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, str. 461—488, CiteSeerX 10.1.1.102.755
 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21.
, ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21. - Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037.
- Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ur.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, str. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208.
- Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688
Spoljašnje veze[uredi | uredi izvor]
- Weisstein, Eric W. „Prism”. MathWorld.
- Paper models of prisms and antiprisms Free nets of prisms and antiprisms
- Paper models of prisms and antiprisms Using nets generated by Stella