Квадратна једначина
Квадратна једначина је у математици полиномијална једначина другог степена. Имплицитни облик потпуне квадратне једначине гласи:
где је a ≠ 0. (За a = 0, једначина постаје линеарна.)
Слова a, b, и c се називају коефицијентима: квадратни коефицијент a је коефицијент уз x2, линеарни коефицијент b је коефицијент уз x, а c је слободан члан.
Квадратна једначина увек има два решења.

Квадратна формула[уреди | уреди извор]
Квадратна једначина са реалним (или комплексним) коефицијентима има два (не обавезно различита) решења, која се називају коренима. Решења могу бити реална или комплексна, а дата су формулом:
где ± означава да су и
и
решења дате квадратне једначине.
Дискриминанта[уреди | уреди извор]

■ <0: x2+1⁄2
■ =0: −4⁄3x2+4⁄3x−1⁄3
■ >0: 3⁄2x2+1⁄2x−4⁄3
У горњој формули, испод квадратног корена присутан израз:
се назива дискриминантом квадратне једначине.
Квадратна једначина са реалним коефицијентима може имати један или два различита реална корена, или два различита комплексна корена. У овом случају, дискриминанта одређује број и природу корена. Постоје три случаја:
- Ако је дискриминанта позитивна добијају се реална и различита решења. Код квадратних једначина са целобројним коефицијентима, ако је дискриминанта савршен квадрат, онда су корени рационални бројеви, док у осталим случајевима могу бити ирационални.
- Ако је дискриминанта једнака нули, постоји само једно решење једначине, и оно је реалан број. Он се некада назива двоструким кореном, а његова вредност је:
- Ако је дискриминанта негативна, решења су комплексни бројеви, и постоје два различита комплексна корена, који су комплексни конјугати један другог:
Дакле, корени су различити ако и само ако је дискриминанта различита од нуле, а реални су ако и само ако дискриминанта није негативна.
Геометрија[уреди | уреди извор]
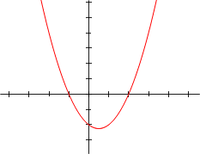
f (x) = x2 − x − 2 = (x + 1)(x − 2) реалне променљиве x, x-координате тачака где график додирује x-осу, x = −1 и x = 2, су корени квадратне једначине: x2 − x − 2 = 0.
Корени квадратне једначине
су такође нуле квадратне функције:
јер су то вредности x за које је
Ако су a, b и c реални бројеви, и домен функције f је скуп реалних бројева, онда су нуле функције f тачно x-координате тачака где график функције додирује x-осу.
Из овога следи да ако је дискриминанта позитивна, график додирује x-осу у две тачке, ако је дискриминанта једнака нули, онда је додирује у једној тачки, а ако је негативна, онда график не додирује x-осу.
Квадратна факторизација[уреди | уреди извор]
Вредност
дели полином
ако и само ако је r корен квадратне једначине
Из квадратне формуле следи да
У посебном случају када квадратна једначина нема два различита корена (то јест, када је дискриминанта једнака нули), квадратни полином се може фактористи као
Примена на једначине вишег реда[уреди | уреди извор]
Одређене једначине вишег реда се могу лако решити помоћу квадратних једначина. На пример:
се може записати као
где је
- .
Највећи експонент мора бити двоструко већи од експонента средњег сабирка. Ова једначина се може решити директно или коришћењем једноставне смене, помоћу метода за решавање квадратних једначина.
Уопштено говорећи, ако је полином квадратни за неку променљиву u где је
онда се квадратна једначина може користити за лакше проналажење решења.
Историја[уреди | уреди извор]
Вавилонски математичари су знали да реше задатке у којима се тражила површина или странице правоугаоника, већ око 1800. године пр. н. е, као што показују сачуване глинене таблице из времена Старог вавилонског царства. Постоје докази на основу којих се тај поступак датира чак у време владавине III династије Ура.[1] У савременој нотацији, задаци су, обично, подразумевали решавање система који су чиниле две једначине облика:
а које су еквивалентне једначини:[2]:86
Вавилонски писари наводе следеће кораке за решавање споменутог проблема одређивања непознатих елемената правоугаоника:
- Израчунати половину од p.
- Квадрирати добијени резултат.
- Одузети q.
- Одредити квадратни корен добијеног броја коришћењем таблице квадрата.
- Сабрати резултате добијене у корацима (1) и (4) како би се добило x. У суштини, овај поступак је еквивалентан коришћењу формуле .
Геометријске методе за решавање квадратних једначина коришћене су у Вавилону, Египту, Грчкој, Кини и Индији. Египатски папирус који датира негде из времена Средњег краљевства (од 2050. п. н. е. до 1650. п. н. е.) а данас се чува у Берлину, па је познат као Берлински папирус, даје решење непотпуне квадратне једначине која има два члана.[3] У индијским списима Шулба султре, око 8. века п. н. е., квадратне једначине облика ax2 = c and ax2 + bx = c су испитиване коришћењем геометријских метода. У Старом Вавилону око 400. п. н. е. и у Кини око 200. п. н. е. у употребу улази геометријска метода дисекције за решавање квадратних једначина са позитивним коренима.[4][5] Правила за решавање квадратних једначина могу се наћи у старокинеском математичком тексту под називом Девет књига о математичкој вештини.[5][6] Ни у једном од тих раних геометријских метода коришћених за одређивање решења квадратне једначине нема назнака опште формуле. Грчки математичар Еуклид нашао је, око 300. п. н. е., апстрактнији геометријски начин за решавање. Захваљујући чисто геометријском приступу Питагора и Еуклид заслужни су за проналажење општег начина одређивања решења квадратне једначине. Грчки математичар Диофант решио је квадратну једначину у својој Аритметици, али је дао само један корен, чак и у ситуацијама када су оба корена позитивна.[7]
Године 628., Брамагупта је дао прво експлицитно (мада још увек не потпуно опште) решење квадратне једначине:
| „ | Апсолутном броју помноженим четири пута [коефицијентом] квадрата, додај квадрат [коефицијента] средњег члана; квадратни корен овога, мање [коефицијент] средњег члана подељен двоструким [коефицијентом] квадрата је вредност. (Brahmasphutasiddhanta (Colebrook translation. 1817. pp. 346) | ” |
Ово је еквивалентно са:
Образац за рачунање корена квадратне једначине[уреди | уреди извор]
Начин извођења обрасца за проналажење решења квадратне једначине може се видети у следећем примеру:
Дата је квадратна једначина са реалним коефицијентима :
Сада ћемо поделити целу једначину са првим коефицијентом (односно поделићемо је са :)
У следећем кораку је потребно направити квадрат бинома:
Затим се познате пребаце на десну страну:
Среди се десна страна:
Сада је потребно изразити :
Односно, то је:
И када се пребаци на десну страну:
И на крају када се среди, добија се познати образац за израчунавање корена квадратне једначине:
Бакшали рукопис из Индије, датиран у 7. век је садржавао алгебарску формулу за решавање квадратних једначина. Мухамед Ал Хорезми (Персија, 9. век) је развио скуп формула које су радиле за позитивна решења. Абрахам бар Хија (познат и под латинским именом Савасорда) је у Европи увео комплетно решење у својој књизи Liber embadorum из 12. века. Баскара II (1114. – 1185), индијски математичар и астроном, је дао прво опште решење квадратне једначине са два корена.[8]
Списи кинеског математичара Јанг Хуија (1238—1298) су први у којима се појављују квадратне једначине са негативним коефицијентима од 'x', мада он ово приписује Лиу Јиу.
Види још[уреди | уреди извор]
- Линеарна једначина
- Кубна једначина
- Основна теорема алгебре
- Парабола
- Квадратна функција
- Чакравалин метод
- Допуна до потпуног квадрата
Референце[уреди | уреди извор]
- ^ Friberg, Jöran (2009). „A Geometric Algorithm with Solutions to Quadratic Equations in a Sumerian Juridical Document from Ur III Umma”. Cuneiform Digital Library Journal. 3.
- ^ Stillwell 2004, стр. 542
- ^ The Cambridge Ancient History Part 2 Early History of the Middle East. Cambridge University Press. 1971. стр. 530. ISBN 978-0-521-07791-0.
- ^ Henderson, David W. „Geometric Solutions of Quadratic and Cubic Equations”. Mathematics Department, Cornell University. Приступљено 28. 4. 2013.
- ^ а б Aitken, Wayne. „A Chinese Classic: The Nine Chapters” (PDF). Mathematics Department, California State University. Приступљено 28. 4. 2013.
- ^ Smith 1958, стр. 380
- ^ Smith 1958, стр. 134.
- ^ h2g2 - The History Behind The Quadratic Formula, Приступљено 8. 4. 2013.
Литература[уреди | уреди извор]
- Smith, David Eugene (1958). History of Mathematics. Courier Dover Publications. стр. 380. ISBN 978-0-486-20430-7.
- The Cambridge Ancient History Part 2 Early History of the Middle East. Cambridge University Press. 1971. стр. 530. ISBN 978-0-521-07791-0.
- Stillwell, John (2004). Mathematics and Its History (2nd ed.). Springer. стр. 542,86. ISBN 978-0-387-95336-6.
- Boyer, Carl Benjamin (1949). . Hafner. Dover edition. Boyer, Carl Benjamin (1959). The History of the Calculus and its Conceptual Development. Dover. ISBN 978-0-486-60509-8.
- Courant, Richard. ISBN 978-3-540-65058-4. Introduction to calculus and analysis 1.
- Robert A. Adams. 1999. ISBN 978-0-201-39607-2. Calculus: A complete course.
- Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985–1986 Survey, Mathematical Association of America No. 7.
- Cliff Pickover. 2003. ISBN 978-0-471-26987-8. Calculus and Pizza: A Math Cookbook for the Hungry Mind.
- Michael Spivak. (September 1994). ISBN 978-0-914098-89-8. Calculus. Publish or Perish publishing.
- Tom M. Apostol. 1967. ISBN 978-0-471-00005-1. Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley.
- Tom M. Apostol. 1969. ISBN 978-0-471-00007-5. Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley.
- Silvanus P. Thompson and Martin Gardner. 1998. ISBN 978-0-312-18548-0. Calculus Made Easy.
- Mathematical Association of America. (1988). Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.
- Thomas/Finney. 1996. ISBN 978-0-201-53174-9. Calculus and Analytic geometry 9th, Addison Wesley.
- Howard Anton, Irl Bivens, Stephen Davis:"Calculus", John Willey and Sons Pte. Ltd. 2002. ISBN 978-81-265-1259-1.
- Larson, Ron, Bruce H. Edwards Calculus, , Brooks Cole Cengage Learning. (9th изд.). 2010. ISBN 978-0-547-16702-2.
- McQuarrie, Donald A. (2003). Mathematical Methods for Scientists and Engineers. University Science Books. ISBN 978-1-891389-24-5.
- Salas, Saturnino L.; Hille, Einar; Etgen, Garret J. (2007). Calculus: One and Several Variables (10th изд.). Wiley. ISBN 978-0-471-69804-3.
- Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano Calculus, , Addison-Wesley. (11th изд.). 2008. ISBN 978-0-321-48987-6.
- Boelkins, M. (2012). Active Calculus: a free, open text (PDF). Архивирано из оригинала 30. 5. 2013. г. Приступљено 1. 2. 2013.
- Crowell, B. (2003). "Calculus". Light and Matter, Fullerton. Приступљено 6 May 2007 from http://www.lightandmatter.com/calc/calc.pdf
- Garrett, P. (2006). "Notes on first year calculus". University of Minnesota. Приступљено 6 May 2007 from http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf
- Faraz, H. (2006). "Understanding Calculus". Приступљено 6 May 2007 from UnderstandingCalculus.com, URL http://www.understandingcalculus.com (HTML only)
- Keisler, H.J. (2000). "Elementary Calculus: An Approach Using Infinitesimals". Приступљено 29 August 2010 from http://www.math.wisc.edu/~keisler/calc.html
- Mauch, S. (2004). "Sean's Applied Math Book" (pdf). California Institute of Technology. Приступљено 6 May 2007 from https://web.archive.org/web/20070614183657/http://www.cacr.caltech.edu/~sean/applied_math.pdf
- Strang, G. (1991). "Calculus" Massachusetts Institute of Technology. Приступљено 6 May 2007 from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm Архивирано на сајту Wayback Machine (25. фебруар 2010)
- Smith, William V. (2001). "The Calculus". Приступљено 4 July 2008 [1] (HTML only).
Спољашње везе[уреди | уреди извор]
- Hazewinkel Michiel, ур. (2001). „Quadratic equation”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104.
- Weisstein, Eric W. „Quadratic equations”. MathWorld.
- 101 uses of a quadratic equation Архивирано на сајту Wayback Machine (10. новембар 2007)
- 101 uses of a quadratic equation: Part II Архивирано на сајту Wayback Machine (22. октобар 2007)





































