Квадратура круга

Квадратура круга је појам везан за најпознатији антички математички проблем. То је скраћени назив за проблем који се најчешће описује реченицом:
Сам назив је опис математичког поступка конструкције квадрата исте површине као и круг. Битно је нагласити да су Хелени преферирали конструкцију, а не нумеричко израчунавање.
Пошто је површина квадрата , а површина круга тада из једнакости површина произилази да је . Још су Хелени умели да геометријски помноже два броја, тј две дужи, односно да геометријски нађу квадратни корен броја, али је за решавање овог проблема потребно геометријски конструисати број π. Геометријска конструкција броја π је немогућа, а то је тек 1882. године показао Линдеман доказујући да π није алгебарски већ трансцендентан број.
Израз квадратура круга у свакодневном животу метафора и означава нерешив проблем, мада је неки користе за опис безнадежног или бесмисленог. Претпоставља се да је на овај проблем током људске историје потрошено више интелектуалног напора него за слање човека на Месец.
У ствари, постоје егзактна решења, али ако се не поштују правила конструкције лењиром и шестаром. Лењиром и шестаром је могуће урадити приближну конструкцију, са извесним степеном апроксимације.
Ово важи за еуклидску геометрију, у нееуклидској геометрији је формула за површину круга другачија па је и квадратура круга могућа у неким случајевима.
Не треба поистовећивати овај проблем са проблемом квадратуре круга Тарског.
Древне квадратуре[уреди | уреди извор]
Први покушај квадратуре круга можемо наћи још код Старих Египћана у Ахмесовом папирусу, око 1650. г п. н. е. Ахмес пише да треба конструисати квадрат од 8/9 пречника круга.
Хелени су први дефинисали овај проблем на прецизан начин. Признавали су решење које поштује правила конструкције лењиром и шестаром. Први Хелен који се бавио квадратуром круга је Анаксагора, додуше у затвору, као богохулни филозоф.
Следећи квадратураши (грч. τετραγωσιειν) Антифон и Брисон разматрају квадратуру али њихови списи су изгубљени. Многи Хелени после њих покушавају, али не успевају. Они су макар били изузетно поштени и професионални и нису подваљивали и варали у тврдњи да су успели.
Архимед није решио квадратуру, али је први утврдио да је површина круга једнака површини правоуглог троугла чија је једна катета једнака полупречнику а друга обиму круга. Приказао је особине спирале којом се може извршити квадратура, али је то решење убројано у механичка.
Од 1050. г, када је Франко од Лижа објавио књигу De quadratura circuli где наводи конструкцију квадратуре у којој је π=22/7, до данашњих дана број људи који су јурили славу објављујући да су коначно решили најтежи математички проблем свих времена је огроман. Париска Академија 1775. године објављује да престаје да прима и разматра пријаве у вези квадратуре круга. Број превараната аматера и даље наставља да расте, па је за ову област дат назив псеудоматематика.
Геометријска квадратура[уреди | уреди извор]
Хелени нису нумерички него геометријски решавали проблем. Били су изузетно вешти и мудри. Када се проблем није успео савладати шестаром и лењиром, пронашли су извесне криве, занимљивих особина, које су се могле користити за решење разних проблема па и квадратуру круга. Сигурно знамо за следеће криве:
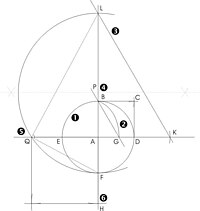
Хипиасова квадратриса[уреди | уреди извор]
Проналазак ове криве се приписује Хипиасу, али се прва успешна демонстрација на конструкцију квадратуре круга приписује Диностратусу.
Поступак квадратуре: Конструише се јединични круг и опише квадрат око њега. Конструише се квадратриса. Израчуна се реципрочна вредност од AG=2/π и помножи са 2 што је AL=π. Опише се круг да би се израчунао корен из π. Са том страницом се коначно конструише квадрат једнак кругу, што је и требало показати.
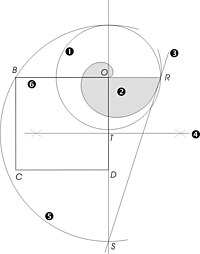
Архимедова спирала[уреди | уреди извор]
Први је открио Конон, али је Архимед описао бројне особине и, међу њима, примена на проблем квадратуре круга.
Поступак квадратуре: Конструише се јединични круг и у њему спирала која чини један пун обрт пре него што пресече круг. Из тачке пресека се повуче тангента на спиралу. Повуче се нормала на полупречник у тачки пресека и добије се тачка S. Сада је OS=π. Опише се круг TS да би се израчунао корен из π. Са том страницом се конструише квадрат једнаке површине као и круг, што је и требало показати.
Међутим ове методе су проглашаване механичким, јер су за цртање тих кривих линија морале бити конструисане посебне механичке направе, пошто лењир и шестар нису били довољни.
Нумеричка квадратура[уреди | уреди извор]
Ово је метода у којој се π апроксимира неким разломком или алгебарском вредношћу до неке жељене тачности па се приступа конструкцији таквог броја.
- Међу најбоље апроксимације спада једна стара од пољског језуитског свештеника Кочанског око 1685. године (конструкција)
- Рамануџан (1913) и Олдс (1963) су описали конструкцију за .
- Диксон (1991) је дао конструкцију у којој је
, где је φ златни пресек и
.
Модерне преваре, преваранти и друге бесмислице[уреди | уреди извор]
Током 20. века је рекорд највише издатих текстова о квадратури круга држао извесни Џејмс Смит. За њега важи да није на основу добрих претпоставки извлачио погрешне закључке већ да његови закључци немају везе са претпоставкама. Његова упорност да докаже да је π=25/8 је резултовала бројним књигама на ту тему.
Де Морган је 1872. године предложио да светац заштитник квадратураша круга буде Свети Вид. Постоји плес посвећен овом свецу у коме учесници вриште и урлају, вртећи се у круг, што води до масовне хистерије. Такође је предложио да лекари прихвате нову дијагнозу morbus cyclometricus за људе обузете квадратуром круга.
Скупштина Савезне државе Индијане је 5. фебруара 1897. године предложила закон којим се проглашава званична вредност броја π која се има употребљавати у држави Индијани. Извесни Едвард Гудвин, предлагач, је закон тако лоше написао да се спомињу четири различите вредности за π али је за сваки случај заштитио своје откриће копирајтом. Аутор је великодушно понудио држави да користи његову вредност за π у школским уџбеницима без надокнаде док би сви остали плаћали тантијеме. Закон је прошао доњи дом једногласно (са 76:0) али је заустављен у горњем дому. Нико не зна да ли је закон икад скинут са дневног реда или још чека на изгласавање.
Данас више нису у питању само аматери, већ предузимљиве особе које своје проналаске штите патентима.








