Ленард-Џоунсов потенцијал
| Рачунарска физика |
|---|
 |
|
Нумеричка анализа · Рачунарска симулација Анализа података · Научна визуелизација |
Ленард-Џоунсов потенцијал је један од физичкохемијских модела којим се описује зависност енергије узајамног деловања неутралних честица од њиховог међусобног растојања. Назван је по свом аутору Џону Ленард-Џоунсу.
Између неутралних честица (атома и молекула) делује сила која, зависно од њиховог међусобног растојања, може бити привлачна или одбојна. На великим растојањима сила је привлачна (ван дер Валсова сила или дисперзиона сила или Лондонова сила) а на малим сила је одбојна. Привлачна сила последица је покретљивости атомског и молекулског наелетрисања због чега неутралне честице могу једна у другој да индукују диполе који се међусобно привлаче. Потенцијална енергија у пољу привлачне силе је негативна. Међутим, на кратким растојањима када наелетрисања из различитих честица почну да се прекривају долази до одбијања честица. Потенцијал у пољу одбојне силе је позитиван. Ленард-Џоунсов потенцијал представља једноставан математички модел у којем је укупни потенцијал међуделовања приказан збиром потенцијала привлачне и одбојне силе. Џон Ленард-Џоунс са универзитета у Бристолу предложио је формулу 1931. године.[1]
Једначина[уреди | уреди извор]
Ленард-Џоунсов потенцијал има два члана, позитивни којим се представља одбијање и негативни којим се представља привлачење међу неутралним честицама:
Овде представља дубину поенцијалне јаме а је радијус честице представљене као чврста сфера. Дакле, члан означава одбојну силу а члан привлачну.
Минимум Ленард-Џоунсовог потенцијала постиже се када се деловања привлачне и одбојне силе узајамно пониште. Растојање при којем се то дешава називамо равнотежним:
- .
Сила је негативни градијент потенцијала поља па из горњег израза налазимо зависност силе од растојања:
Ленард-Џоунсов потенцијал је приближни потенцијал. Облик одбојног члана нема теоријског оправдања; одбојни члан би требало експоненцијално да пада са растојањем. Међутим зависност коју је педложио Ленард-Џоунс је згодна јер се лао израчунава (онд аније било рачунара) као квадрат привлачног члана, . Привлачни потенцијал који има далеки домет изведен је из Лоноднове дисперзионе силе.
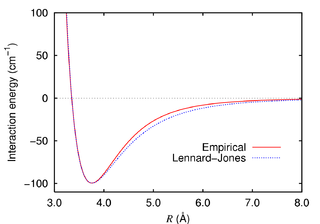
Ленард-Џоунсов потенцијал је релативно добра апроксимација и због једноставности често се користи за описивање гасова, и моделовање дисперзије и преклапања у молекулским моделима. Посебно је згодан за описивање атома инертних гасова а добра је апроксимација при великим и средњим растојањима код неутралних молекула. На цртежу је приказан потенцијал за димер аргона, у поређењу са емпиријским потенцијалом. Мало неслагање последица је нетачности у одбојном делу Ленард-Џоунсовог потенцијала.
Алтернативни изрази[уреди | уреди извор]
Функција Ленард-Џоунсовог потенцијала често се изражава и као
где је
- = равнотежно растојање (растојање на минимуму потенцијала).
Често се користи и облик
где је
и
- .
Референце[уреди | уреди извор]
- ^ Lennard-Jones, J. E. Cohesion. Proceedings of the Physical Society 1931, 43, 461-482.









![{\displaystyle V(r)=\epsilon \left[\left({\frac {r_{min}}{r}}\right)^{12}-2\left({\frac {r_{min}}{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/559839c917103b2e6bc1bbe0dc03d49bab81ce90)






