Непрекидна функција

Интуитивно, непрекидна функција је она функција, која за довољно мале промене вредности аргумента има произвољно мале промене вредности функције. Такође, интуитивно, непрекидну функцију замишљамо као функцију чији график можемо нацртати не подижући оловку са папира.

Непрекидност функције је појам везан за топологију, где је непрекиднст функција реалних бројева је специјалан случај. За функцију која није непрекидна кажемо да је прекидна, тј. да има прекид.

Дефиниције

За више информација погледајте чланак Дефиниције непрекидности

Кошијева дефиниција

Илустровани приказ Кошијеве ε - δ дефиниције непрекидности. За нпр. ε=0.5, c=2, вредност δ=0.5 задовољава услов дефиниције.

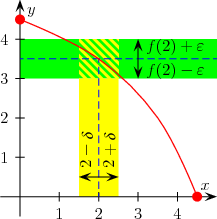
Кошијева дефиниција је дефиниција на $\varepsilon - \delta$ језику, и везана је за функције реалних бројева.

Посматрајмо функцију $f:X\rightarrow\mathbb{R},X\subseteq\mathbb{R}$. Нека је $x_0 \in X$ тачка нагомилавања скупа $X$.

Функција $f$ је непрекидна у тачки $x_0$, ако је:

$(\forall \varepsilon > 0)(\exists \delta > 0)(\forall x \in X)(|x - x_0| < \delta \Rightarrow |f(x) - f(x_0)| < \varepsilon)$

Ова дефиниција је еквивалентна са:

Функција $f$ је непрекидна у тачки $x_0$, ако је:

$\lim_{x\rightarrow x_0} f(x)=f(x_0)$

Хајнеова дефиниција

Овом дефиницијом описана је непрекидна функција преко граничне вредности низа.

Реална функција $f$ је непрекидна ако за сваки низ $(x_n)_{n\in \mathbb{N}}$, такав да

$\lim_{n\rightarrow \infty} x_n = L$,

важи

$\lim_{n\rightarrow \infty} f(x_n) = f(L)$

Овде смо наравно претпоставили да сваки члан низа припада домену функције.

Тополошка дефиниција

Функција $f:X\rightarrow\mathbb{R}$ је непрекидна у тачки $x_0\in X$ ако

$(\forall V \in \mathcal{V}(f(x_0)))(\exists U \in \mathcal{V}(x_0))(f(U \cap X) \subseteq V)$

Непрекидност са стране

Функција непрекидна с десне стране

Посматрајмо функцију $f:X\rightarrow\mathbb{R}$,

функција је непрекидна са леве стране у тачки $x_0$ ако

$\lim_{x\rightarrow x_0-0} f(x)=f(x_0)$

функција је непрекидна са десне стране у тачки $x_0$ ако

$\lim_{x\rightarrow x_0+0} f(x)=f(x_0)$

Теорема: Функција $f:X\rightarrow\mathbb{R}$ је непрекидна у тачки $x_0\in X$ ако и само ако је непрекидна у тој тачки и са леве и са десне стране.

Непрекидност на скупу

Функција $f$ је непрекидна на скупу $X \subseteq \mathbb{R}$ ако је непрекидна у свакој тачки тог скупа, односно на $\varepsilon - \delta$ језику:

$( \forall x_0 \in X)( \forall \varepsilon > 0)( \exists \delta > 0)( \forall x \in X)( | x - x_0 | < \delta \Rightarrow | f ( x ) - f ( x_0 ) | < \varepsilon )$

Униформна непрекидност

Функција $f: X \rightarrow \mathbb{R}$ је униформно непрекидна на скупу $X$ ако

$( \forall \varepsilon > 0)( \exists \delta > 0)( \forall x_1, x_2 \in X)( | x_1 - x_2 | < \delta \Rightarrow | f(x_1) - f(x_2) | < \varepsilon )$

Локална својства непрекидниих функција

Под локалним својствима непрекидне функције се подразумевају својства функције која су уско повезана са понашањем функције у околини неке тачке непрекидности.

Глобална својства непрекидних функција

Глобална својства непрекидне функције се односе на понашање функције у неком непрекидном интервалу дефинисаности.

Дефиниција: Функција $f: X \rightarrow \mathbb{R}, X \subseteq \mathbb{R}$ је непрекидна на неком скупу $X$ ако је непрекидна у свакој тачки тог скупа.

Функција је део-по-део непрекидна на скупу $[a,b]$ ако постоји коначно много тачака $a = x_0 < x_1 < x_2 < ... < x_n = b$ тако да је функција дефинисана на сваком сегменту $(x_i, x_{i+1}), i = {0, 1, 2, ..., n-1}$ и на крајевима тих интервала има одговарајуће лимесе.

Болцано-Кошијева теорема о међувредности

Нека је дата непрекидна функција $f: [a,b] \rightarrow \mathbb{R}$ и нека је $f(a) = A$ и $f(b) = B$. Ако је $C$ произвољна вредност између $A$ и $B$, онда постоји тачка $c \in [a,b]$ за коју важи: $f(c) = C$.

Специјално, ако функција $f$ узима вредности различитих знакова на крајевима сегмента $[a,b]$, тј. ако је $f(a) \cdot f(b) <0$, онда постоји тачка $c \in [a,b]$ тако да је: $f(c) = 0$.

Вајерштрасова теорема о ограничености непрекидне функције

Ако је функција $f : [a,b] \rightarrow \mathbb{R}$ непрекидна на $[a,b]$, она је и ограничена на $[a,b]$ и постоје тачке у оквиру тог сегмента у којима она достиже своју максималну и минималну вредност на сегменту.

Непрекидност код елементарних функција

Види елементарне функције

Теорема: Све елементарне функције су непрекидне на свом природном домену.

Литература

• Душан Аднађевић, Зоран Каделбург: Математичка анализа 1, Студентски трг, Београд, 1995.

Види још

• Функција
• Математичка анализа
• Гранична вредност функције
• Елементарна функција
• Униформна непрекидност

Спољашње везе

Викимедијина остава има још мултимедијалних датотека везаних за: Непрекидна функција