Фрешеова раздаљина
У математици, Фрешеова раздаљина је мера сличности између кривих која узима у обзир локације и редослед тачака на кривама. Добила је име по Морису Фрешеу.
Интуитивна дефиниција[уреди | уреди извор]
Фрешеова раздаљина између 2 криве је минимална дужина повоца потребна да се повежу пас и његов власник, смештених на 2 одвојене стазе, док се крећу искључиво напред дуж својих појединачних путања од једног краја до другог. Дефиниција је симетрична у односу на две криве. Замислите пса како иде једном путањом и његовог власника како иде другом путањом, а повезани су повоцем. Обоје се крећу непрекидно дуж својих појединачних кривих од предвиђене почетне тачке до предвиђене крајње тачке путање. Брзина обојице варира, могу и да стану, на произвољној позицији и на произвољно дуго време. Међутим, морају се искључиво кретати напред. Фрешеова раздаљина између 2 криве је дужина најкраћег повоца (не најкраћег повоца који је довољан за било какво кретање, већ најкраћег од свих поводаца) који је довољан да се повежу обе криве на овај начин.
Формална дефиниција[уреди | уреди извор]
Нека је метрички простор. Крива у је непрекидна функција из јединичног интервала у , нпр., . A, репараметризација из је непрекидна, монотона функција, сурјекција .
Нека су и две дате криве . Онда, Фрешеова раздаљина између и се дефинише као инфимум свих репараметризација и из максимума од свих раздаљина у између и . У математичком запису, Фрешеова раздаљина је
где је функција раздаљине у .
Неформално, можемо да посматрамо параметар као "време". Онда, је позиција пса, а позиција његовог власника у тренутку (или обрнуто). Дужина повоца између њих у тренутку је растојање између и . Инфимум свих могућих репараметризација одговара одабиру кретања дуж датих стаза где је максимална дужина повоца најмања могућа. Ограничење да су и неопадајуће значи да се и пас и његов власник могу кретати искључиво напред.
Фрешеова метрика узима у обзир путање 2 криве зато што парови тачака чија раздаљина доприноси Фрешеовој раздаљини непрекидно клизе дуж појединачних кривих. То чини Фрешеову раздаљину бољом мером сличности за криве него алтернативе, као што је Хаусдорфова раздаљина, за произвољне низове тачака. Могуће је да 2 криве имају малу Хаусдорфову, а велику Фрешеову раздаљину.
Фрешеова раздаљина и њене варијанте имају примену у неколико проблема, од специјалних ефеката за филмове и анимације[1] и препознавања рукописа[2] до усклађивања структуре протеина.[3] Алт и Годо[4] су први описали алгоритам у полиномском времену да би израчунали Фрешеову раздаљину између 2 полигонске криве и Еуклидовом простору. Време извршавања њиховог алгоритма је за 2 полигонске криве са m и n сегментима.
Дијаграм у слободном простору[уреди | уреди извор]
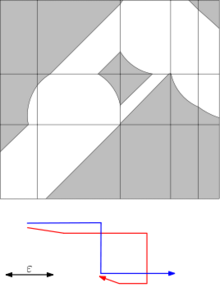
Важан начин рачунања Фрешеове раздаљине 2 криве је дијаграм у слободном простору који су први увели Алт и Годо.[4] Дијаграм у слободном простору између 2 криве за дати праг раздаљине ε је дводимензионална област у параметарском простору који се састоји од свих парова тачака на 2 криве највећег растојања ε:
Фрешеова раздаљина је највише ε ако и само ако дијаграм у слободном простору садржи путању од доњег левог до горњег десног угла, који је монотон и у хоризонталном и у вертикалном правцу.
Варијанте[уреди | уреди извор]
Слаба Фрешеова раздаљина је варијанта класичне фрешеове раздаљине без услова да се крајње тачке крећу монотоно дуж својих кривих — пцу и његовом власнику је дозвољено да се враћају назад да би одржали поводац кратким. Алт и Годо[4] су описали једноставнији алгоритам за израчунавање слабе Фрешеове раздаљине између полигоналних кривих.
Дискретна Фрешеова раздаљина, такозвана паздаљина спојнице, је апроксимација Фрешеове метрике за полигонске криве, које су дефинисанали Ајтер и Манила.[5] Дискретна Фрешеова раздаљина разматра само позиције ужета где су његове крајње тачке лоциране на теменима 2 полигонске криве и никада у унутрашњости ивице. Ова специјална структура дозвољава да се дискретна Фрешеова раздаљина израчуна у полиномном времену лаким алгоритмом динамичког програмирања.
Када су две криве уграђене у метрички простор изузев Еуклидовог простора, као што је полиедарских терен или неки Еуклидов простор са препрекама, растојање између две тачке на кривама најприродније се дефинише као дужина најкраћег пута између њих. Поводац мора да буде геодетски спој његових крајњих тачака. Добијена метрика између кривих се зове геодетско Фрешеово растојање.[1][6][7] Кук и Венк[6] су описали алгоритам за рачунање Фрешеове раздаљине између 2 полигонске криве у многоуглу са непресецајућим страницама у полигоналном времену.
Ако поводац мора непрекидно да се креће у амбијенталном метричком простору, онда добијамо хомотопијску Фрешеову раздаљину[8] између 2 криве. Поводац се може пребацити са једне позиције једино непрекидно у други, али поводац не може прескочити препреке, а може прећи преко планине на терену само ако је довољно дуг. Кретање повоца описује хомотопију између две криве. Чамберс и остали описујуалгоритам у полиномном времену за израчунавање хомотопијске Фрешеове раздаљине између полигоналних кривих у Еуклидовој равни са препрекама.
Примери[уреди | уреди извор]
Фрешеово растојање између 2 концентрична круга полупречника и је Најдужи поводац је потребан када власник стоји а пас оде на супротну страну круга (), а најкраћи поводац је када се обојица крећу константном брзином око круга ().
Референце[уреди | уреди извор]
- ^ а б Efrat, Alon; Guibas, Leonidas J.; Har-Peled, Sariel; Mitchell, Joseph S. B.; Murali, T. M. (2002), „New similarity measures between polylines with applications to morphing and polygon sweeping” (PDF), Discrete and Computational Geometry, 28 (4): 535—569, doi:10.1007/s00454-002-2886-1, Архивирано из оригинала (PDF) 19. 06. 2010. г., Приступљено 08. 06. 2014
- ^ Sriraghavendra, R.; Karthik, K.; Bhattacharyya, Chiranjib (2007), „Fréchet distance based approach for searching online handwritten documents”, Proc. 9th International Conference on Document Analysis and Recognition (ICDAR '07), стр. 461—465, doi:10.1109/ICDAR.2007.121, Архивирано из оригинала 03. 03. 2016. г., Приступљено 08. 06. 2014
- ^ Minghui, Jiang; Ying, Xu; Binhai, Zhu (2008), „Protein structure-structure alignment with discrete Fréchet distance”, Journal of Bioinformatics and Computational Biology, 6 (1): 51—64, PMID 18324745, doi:10.1142/S0219720008003278
- ^ а б в Alt, Helmut; Godau, Michael (1995), „Computing the Fréchet distance between two polygonal curves” (PDF), International Journal of Computational Geometry and Applications, 5 (1–2): 75—91, doi:10.1142/S0218195995000064, Архивирано из оригинала (PDF) 15. 05. 2004. г., Приступљено 08. 06. 2014
- ^ Eiter, Thomas; Mannila, Heikki (1994), Computing discrete Fréchet distance (PDF), Tech. Report CD-TR 94/64, Christian Doppler Laboratory for Expert Systems, TU Vienna, Austria
- ^ а б Cook, Atlas F., IV; Wenk, Carola (2008), Geodesic Fréchet distance with polygonal obstacles (PDF), Tech. Report CS-TR-2008-0010, University of Texas at San Antonio[мртва веза]
- ^ Maheshwari, Anil; Yi, Jiehua (2005), „On computing Fréchet distance of two paths on a convex polyhedron”, Proc. 21st European Workshop on Computational Geometry (PDF), стр. 41—44, Архивирано из оригинала (PDF) 03. 03. 2016. г., Приступљено 08. 06. 2014
- ^ Chambers, Erin Wolf; Colin de Verdière, Éric; Erickson, Jeff; Lazard, Sylvain; Lazarus, Francis; Thite, Shripad (2009), „Homotopic Fréchet distance between curves, or Walking your dog in the woods in polynomial time” (PDF), Computational Geometry: Theory and Applications, 43 (3): 295—311, doi:10.1016/j.comgeo.2009.02.008[мртва веза]



![{\displaystyle A:[0,1]\rightarrow S}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6edd4c77af36de6c609ab6800cce5f57c21742e)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle \alpha :[0,1]\rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3670292977d70d09aa06595f56abffe9173dfa8f)


![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)



![{\displaystyle F(A,B)=\inf _{\alpha ,\beta }\,\,\max _{t\in [0,1]}\,\,{\Bigg \{}d{\Big (}A(\alpha (t)),\,B(\beta (t)){\Big )}{\Bigg \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3395e48df64fa6870dcdc64f6992558789a2a1f7)



![{\displaystyle D_{\varepsilon }(A,B):=\{\,(\alpha ,\beta )\in [0,1]^{2}\mid d(A(\alpha ),B(\beta ))\leq \varepsilon \,\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5528eadf0a7d67fe052cdcf26a27b5a350b19b5)





