Hip (struktura podataka)
| Овај чланак је започет или проширен кроз пројекат семинарских радова. Потребно је проверити превод, правопис и вики-синтаксу. Када завршите са провером, допишете да након |проверено=. |

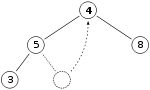
U kompjuterskim naukama, hrpa je struktura podataka organizovana po principu stabla koja mora da zadovoljava uslov hrpe: ključ svakog čvora je veći ili jednak od ključeva njihovih sinova. Kada je maksimalan broj dece jednog čvora dva, to je binarna hrpa.
Hrpa je izuzetno bitan u nekim algoritmima, kao što je Dijkstra algoritam i heapsort. Hrpa je veoma korisna struktura podataka kada treba da se ukloni čvor najvišeg ili najnižeg prioriteta.
Čvor je jedna memorijska jedinica i sadrži kljuc tj, podatak. Svaki čvor ima svog pretka, sem korena stabla koji predstavlja vrh hijerarhije. Ako je čvor A predak cvora B, onda je B potomak od A. Čvor bez potomaka se zove list, a čvor koji nije list se zove unutrašnji čvor. Ključ svakog čvora je uvek veci ili jednaki od kljuceva njegovih potamaka i najveci kljuc je u korenu stabla. Ne postoji posebna veza između čvorova na istom nivou ili braće. Kako je hrpa binarno stablo,ima najmanju moguću visinu - O(log n) za hrpa sa n čvorova. Kako između braće ne postoji veza i čvor je direktno vezan samo sa roditeljem i decom (prvim pretkom i potomcima), ne postoji mogućnost za obilazak stabla.
Hrpa je maksimalno efikasna implementacija apstraktnog tipa podataka koji se zove red sa prioritetom. U stvari redove sa prioritetom cesto nazivaju "hrpom", bez obzira na to kako su implemetirani. Uprkos sličnosti imena "hrpa" sa imenima "stek" i "red",druga dva su apstraktni tip podataka, dok je hrpa specifična struktura podataka i "red sa prioritetom" je pogodan naziva sa apstraktni tip podataka.
Operacije u hrpi[уреди | уреди извор]
Operacije uklanjanja i umetanja elementa se obavljaju tako da se prvo zadovolji svojstvo oblika dodavanjem ili uklanjanjem čvora sa dna stabla, a zatim se sređuje svojstvo hrpe kretanjem po hrpi. Obe operacija zahtevaju vremensku složenost O(log n), što znači da se efikasno izvršavaju.Nedostatak hrpe je što se traženje ključa ne može izvršiti tako jednostavno. Smatraćemo da su ključevi čvorova hrpe smešteni u vektor A,dok je n broj elemenata hrpe. Elementi su na indekisama od 1 do n.
Umetanje[уреди | уреди извор]
- Broj n se uveća za jedan i novi element se upiše na slobodnu poziciju A[n]
- Upoređujemo taj ključ i ključ elementa na poziciji A[i],gde je i=⌊n/2⌋,pa ako je veći od njega,menjaju im se mesta
- Postupak se nastavlja premeštanjem ključa naviše,sve dok n bude manji ili jednak od oca
- Induktivna hipoteza: Ako je umetnuti ključ nakon premeštanja u čvoru A[j], onda je to koren ispravne hrpe i ako se to podstablo ukloni,ostatak stabla zadovoljava uslov hrpe
[уреди | уреди извор]
- ključ najvećeg elementa je A[1], pa ga je lako naći
- zamenimo elemente A[n] i A[1]
- n smanjimo za jedan
- x=A[1] a y=max{A[2], A[3]}(veći od sinova korena)
- ako je x ≥ y,onda je kompletno stablo ispravna hrpa
- inace,posle zamene ključeva elemenata x i y,,podstablo sa nepromenjenim korenom ostaje ispravana hrpa,a u drugom podstablu je promenjen koren
- rekurzivno se sređuje podstablo
- induktivna hipoteza: ako je posle i koraka x na poziciji A[j],onda samo podstablo sa korenom A[j] eventualno ne zadovoljava uslov hrpe. Dalje se x upoređuje sa A[2j] i A[2j+1] i dalje se zamenjuju mesta ako treba.
Vrste hrpe[уреди | уреди извор]
- 2-3 hrpa
- B-hrpa
- Beap
- Binarna hrpa
- Binomna hrpa
- Brodal red
- d hrpa
- Fibonači hrpa
- Leftist hrpa
- Pairing hrpa
- Skew hrpa
- Soft hrpa
- Weak hrpa
- Leaf hrpa
- Radix hrpa
- Randomized meldable hrpa
- Ternary hrpa
- Treap
Poređenje teoretskih granica za varijante[уреди | уреди извор]
O(f) daje asimtotsku gornju granicu i Θ(f) je asimptotski bliska granica(pogledati notaciju veliko O). Radi se sa min-hrpom.
| Operacija | Binarni hip | Binomni hip | Fibonači hip | Pairing hip[1] | Brodal red [2][3]}} | Rank-pairing[4] |
|---|---|---|---|---|---|---|
| naći min | Θ(1) | Θ(1) | Θ(1) | Θ(1) | Θ(1) | Θ(1) |
| izbriši min | Θ(log n) | Θ(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| ubaci | Θ(log n) | O(log n) | Θ(1) | Θ(1) | Θ(1) | Θ(1) |
| smanji ključ | Θ(log n) | Θ(log n) | Θ(1) | O(log n) | Θ(1) | Θ(1) |
| spajanje | Θ(n) | O(log n) | Θ(1) | Θ(1) | Θ(1) | Θ(1) |
Implementacija hrpe[уреди | уреди извор]
Hrpa se može realizovati eksplicitno ili implicitno zadatim stablom.Eksplicitno znači da se koristi struktura podataka koja sadrži ključ i pokazivače ka sinovima(i nekada ka ocu).Implicitno znači da se čvorovi stavljaju u niz i da su njihove veze određene njihovom pozicijom u vektoru.
Implementacija pomoću niza[уреди | уреди извор]
Svako binarno stablo može biti sačuvano preko niza, ali pošto je binarna hrpa skoro uvek kompletno binarno stablo,implementacija pomoću niza,bez pokazivača je pogodna.Pozicija korena moze biti na indexu 0 ili 1.Sledeća dva elementa će da sadrže njegovu decu.Sledeća četiri decu od dva čvora koji su deca od korena itd. Tako da će deca čvora na poziciji n biti na poziciji 2n i 2n+1. Ovo omogućava pomeranje elemenata koristeći proračune indexa.Balansiranje hrpe se radi zamenjivanjem elemenata koji nisu na mestu.Kako možemo da napravimo hrpu od niza bez korišćenja dodatne memorije(za čvorove npr),heapsort može da bude korišćen za sortiranje nizova u mestu. Ova implementacija se koristi kod heapsort algoritma za sortiranje gde je dozvoljeno da se prostor u ulazni niz ponovo iskoristi za čuvanje hrpe. Algoritam vrši sortiranje u mestu. Implementacija je takođe korisna kao i red sa prioritetom gde korišćenje dinamičkog niza dozvoljava ubacivanje neograničenog broja članova.
Primena[уреди | уреди извор]
- Heapsort: Jedan od najboljih metoda za sortiranje u mestu bez kvadratne složenosti za najgore slučajeve.
- Algoritem izbora: Hrpa dozvoljava pristup najvećem i najmanjem elementu u konstantnom vremenu,a ostalim selekcijama (kao što su medijana i k-ti element) u sub-linearnom vremenu nad podacima koji su u hrpi.[5]
- Grefovski algoritmi:Koristeći hrpu kao internu strukturu podataka, vreme izvršavanja može biti smanjeno polinomijano. Primari takvih problema su Primov algoritam i Dijkstrin algoritam.
- Red sa prioritetom: Red sa prioritetom je apstraktni koncept kao "lista" ili "mapa";Kao što lista može biti implemetirana povezanom listom ili kao niz,red sa prioritetom može biti implemetiran pomoću hrpe ili drugih metoda.
- Statistika reda: Struktura podataka heap može da se koristi za efikasno pronalaženje k-tog najmanjeg (ili najvećeg) elementa u nizu.
Reference[уреди | уреди извор]
- ^ Iacono, John (2000), „Improved upper bounds for pairing heaps”, Proc. 7th Scandinavian Workshop on Algorithm Theory, Lecture Notes in Computer Science, 1851, Springer-Verlag, стр. 63—77, doi:10.1007/3-540-44985-X_5
- ^ http://www.cs.au.dk/~gerth/papers/soda96.pdf
- ^ Goodrich, Michael T.; Tamassia, Roberto (2004). „7.3.6. Bottom-Up Heap Construction”. Data Structures and Algorithms in Java (3rd изд.). стр. 338—341.
- ^ Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (2009). „Rank-pairing heaps” (PDF). SIAM J. Computing: 1463—1485. Архивирано из оригинала (PDF) 21. 04. 2014. г. Приступљено 20. 04. 2014.
- ^ Frederickson, Greg N. (1993), „An Optimal Algorithm for Selection in a Min-Heap”, Information and Computation (PDF), 104 (2), Academic Press, стр. 197—214, doi:10.1006/inco.1993.1030, Архивирано из оригинала (PDF) 03. 12. 2012. г., Приступљено 19. 04. 2014
Spoljašnje veze[уреди | уреди извор]
- Heap at Wolfram MathWorld
- "Algoritmi" Miodrag Živković