Samoorganizovana lista
| Овај чланак је започет или проширен кроз пројекат семинарских радова. Потребно је проверити превод, правопис и вики-синтаксу. Када завршите са провером, допишете да након |проверено=. |
Samoorganizovana lista je lista kod koje se elementi raspoređuju na osnovu samoorganizovanog heurističnog algoritma koji poboljšava prosečno vreme pristupa. Cilj ovakve liste je da se poboljša efikasnost linearne pretrage pomeranjem češće pristupanim elementima ka prednjem kraju liste. Lista samo-organizovanja ostvaruje gotovo konstantno vreme za pristup elementima u najboljem slučaju. Koristi se algoritam za prepoznavanje kako bi se prilagodila različitim vrstama zahteva u toku rada.
Istorija[уреди | уреди извор]
Koncept samoorganizovanih listi uveo je McCabe 1965.[1] godine. U ranom periodu on je predstavio dve heuristike - Pomeranje ka prednjem kraju (eng. Move to Front Method (MTF)) i Pravilo zamene (eng. Transpose Method). Vremenom, pravljena su različita poboljšanja, a algortime su pronalazili Ronald Rivest, Tenenbaum i Nemes, D. Knuth i drugi.
Uvod[уреди | уреди извор]
Najjednostavnija implementacija samoorganizovane liste je u obliku povezane liste. Ovaj način je efikasan u slučajnom umetanju čvora i alokaciji memorije, ali trpi zbog neefikasnog pristupa tim slučajnim čvorovima.
Nefikasnost samoorganizovanih listi[уреди | уреди извор]
Ako poseban čvor treba da se pronađe u listi, svakom čvoru u listi mora sekvencijalno da se pristupi dok se ne dostigne željeni čvor. U povezanoj listi, za pronalaženje n-tog elementa potrebno je O(n) operacija. Ovo je veoma neefikasno u poređenju sa nizovima gde je, na primer, pristup n-tom elementu O(1) operacija.
Efikasnost samoorganizovanih listi[уреди | уреди извор]
Samoorganizovana lista čuva čvorove kojima se najčešće pristupa na vrhu liste. Generalno , u određenom upitu , šanse za pristupanje čvoru kojem je ranije pristupljeno mnogo puta veće su nego šanse za pristup nekom čvoru kojem ranije nije tako često pristupano. Kao rezultat toga, držeći najčešće pristupane čvorove na prednjem kraju liste rezultuje smanjenom broju poređenja potrebnih, u prosečnom slučaju, da se dostigne željeni čvor. To dovodi do bolje efikasnosti i generalno smanjenom broju upita.
Implementacija samoorganizovanih listi[уреди | уреди извор]
Implementacija i metode samoorganizovanih listi su identični sa onima za standardnu povezanu listu. Povezana lista i samoorganizovana lista se razlikuju samo u pogledu organizovanja čvorova, interfejs ostaje isti.
Analiza vremena potrebnog za pristup/pretragu u listi[уреди | уреди извор]
Prosečan slučaj[уреди | уреди извор]
Može se pokazati da u prosečnom slučaju, vreme potrebno za pretragu u samoorganizovanoj listi veličine n je:
gde je p(i) verovatnoća pristupa i-tom elementu u listi; Ako je verovatnoća pristupa svakog elementa ista ( tj. p(1) = p(2) = p(3) = ... = p(n) = 1/n ), onda je redosled elemenata irelevantan i prosečna vremenska složenost iznosi:
i T(n) ne zavisi od verovatnoće pojedinačnih pristupa elemenatima u listi u ovom slučaju. Međutim, u slučaju pretrage na listi sa nejedinstvenim zapisom verovatnoće pristupa elementima (tj. one liste kod kojih se verovatnoća pristupa jednog elementa razlikuje od drugog), prosečna složenost može biti drastično smanjena pravilnim postavljanjem elemenata sadržanih u listi. To se radi uparivanjem manjeg sa većim verovatnoćama pristupa kako bi da smanjilo ukupnu prosečno vreme složenosti. Ovo može da se pokaže na sledeći način: Data je lista: A(0.1), B (0.1), C (0.3), D (0.1), E (0.4). Bez preraspoređivanja, prosečno vreme potrebno je pretraživanje:
Sada pretpostavimo da su čvorovi preuređene tako da su oni sa najvećom verovatnoćom pristupa postavljeni na prednjem kraju, tako da je sada preuređena lista: E(0.4), C(0.3), D(0.1), A(0.1), B(0.1) Ovde, složenost iznosi:
Tako je prosečno vreme potrebno za traženje u organizovanoj listi je ( u ovom slučaju ) oko 40% manje u odnosu na vreme koje je potrebno za traženje u nasumično uređenoj listi. Ovo je koncept samoorganizovanih listi kod kojih se prosečna brzina preuzimanja podataka povećava sa preraspoređivanjem čvorova prema njihovoj frekvenciji pristupa.
Najgori slučaj[уреди | уреди извор]
U najgorem slučaju, element koji treba pronaći nalazi se na samom kraju liste; bilo to obična ili samoorganizovana lista, mora biti napravljeno n poređenja kako bi se se stiglo do tog elementa. Stoga, u najgorem slučaju vreme izvršavanja linearne pretrage na listi je O(n) nezavisno od tipa liste koji se koristi. Imajte na umu da izraz prosečne složenosti vremena za pretragu u prethodnom odeljku je samo jedna verovatnoća. Zadržavanje elemenata kojima se najčešće pristupa na čelu liste jednostavno smanjuje verovatnoću javljanja najgoreg slučaja, ali ga ne eliminiše u potpunosti! Čak i u samoorganizovanoj listi, ako treba da se pristupi elementu sa najmanjom verovatnoćom pristupa (očigledno smestenom na kraj liste), cela lista mora da se predje. To je najgori slucaj.
Najbolji slučaj[уреди | уреди извор]
U najboljem slučaju, čvor koji tražimo je bas onaj čvor kojem se najčešće pristupa i on predstavlja glavu liste. Ovo će rezultovati gotovo konstatan broj operacija, pa je u - notaciji, u najboljem slučaju, složenost pristupa tom elementu O(1).
Tehnike preraspoređivanja čvorova[уреди | уреди извор]
Tokom postavljanja elemenata u listu, verovatnoće pristupa elementima nisu opšte poznate unapred. Ovo je dovelo do razvoja različitih heuristika da približe optimalno ponašanje. Osnovne heuristike koje se koriste da biste promenili redosled elemenata u listi su:
Pomeranje ka prednjem kraju(MTF metod)[уреди | уреди извор]
Ova tehnika pomera element kojem se pristupa na čelo liste. Prednosti ovoga su relativno jednostavna imlementacija i ne zahteva dodatnu memoriju. Ova heuristika se takođe brzo prilagođava na brze promene u raspodeli upita. S druge strane, ovaj metod može dati prioritet retko pristupanim čvorovima - na primer, ako je nekom čvoru pristupano barem jednom, on se premešta na čelo liste i daje mu se maksimalni prioritet, čak i ako mu se neće često pristupati u budućnosti. Ovi preko nagrađeni čvorovi narušavaju optimalan redosled u listi i dovode do sporijeg vremena pristupa najčešće pristupanim elementima. Još jedna mana je to što ovaj metod može postati previše fleksibilan što dovodi do modela prustupa koji se menjaju suviše brzo. To znači da zbog veoma kratkog sećanja modela pristupa čak i pri optimalnom rasporedu liste, može odmah da se poremeti pristupom nekom čvoru u listi kojem se ne pristupa tako često.
Za i-ti čvor važi:
if čvor i je pristupljen:
premesti i-ti čvor na čelo liste
Metod brojanja[уреди | уреди извор]
U ovoj tehnici, broji se koliko puta je svaki čvor tražen, odnosno svaki čvor vodi posebnu brojačku promenljivu koja se povećava svaki put kada se čvoru pristupi. Čvorovi su zatim raspoređeni u opadajućem redosledu. Dakle, čvorovi sa najvećim brojem, odnosno najčešće pristupani, čuvaju se na čelu liste. Osnovna prednost ove tehnike je da generalno realnije prikazuje stvarni obrazac pristupa. Međutim, postoji dodatni memorijski zahtev, tj prostor za brojačku promenljivu za svaki čvor u listi. Takođe, ova tehnika se ne prilagođava brzom naglim promenama u obrascima pristupa. Na primer: ako brojač za element glave (A) iznosi 100, a za neki drugi čvor nakon njega (B) je 40, onda čak i ako B postane novi najčešće pristupani elemenat, njemu se mora pristupiti najmanje (100 - 40 = 60 ) puta pre nego što on sam može postati glava liste, kako bi redosled liste postao optimalan.
init: count(i) = 0 za svaki čvor i
Za i-ti čvor važi:
if čvor i je pristupljen:
count(i) = count(i) + 1
sortiraj listu prema promenjivoj count(i)
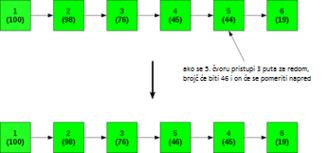
Metod zamene[уреди | уреди извор]
Ova tehnika podrazumeva zamenu čvora kojem se pristupa sa svojim prethodnikom. Prema tome, ako je pristupljeno čvoru, on se menja sa čvorom iza, osim ako je čvor glava; tada samo povećava svoj prioritet. Ovaj algoritam se lako implementira i prostorno je efikasan (ne zahteva dodatan memorijski prostor) i lakše je čuvati češće pristupane čvorove na prednjem delu liste. Međutim, ovaj metod je znatno oprezniji, odnosno potreban je veliki broj pristupa da bi element došao na vrh liste. Ovaj metod takođe ne dozvoljava brze odgovore na nagle promene u raspodeli zahteva za čvorove u listi.
Za i-ti čvor važi:
if čvor i je pristupljen:
if čvor i nije glava liste:
zameni čvor i sa čvorom i-1
Druge metode[уреди | уреди извор]
Istraživanje su se fokusirala na spajanje gore navedenih algoritama za postizanje bolje efikasnosti. Bitnerov algoritam[2] koristi MTF metod u početku, a zatim, za finije preraspodele, koristi metod zamene. Neki algoritmi su nasumični i pokušavaju da spreče "preterano nagrađivanje" čvorova kojima se retko pristupa, koje može nastati u MTF algoritmu. Ostale tehnike uključuju reorganizaciji čvorove na osnovu navedenih algoritama posle svakih n pristupa listi u celini ili posle n pristupa u nizu na određenom čvoru i tako dalje. Neki algoritmi preuređuju čvorove kojima je pristupljeno na osnovu njihove blizine glavi liste, na primer: Zameni sa roditeljem (eng. Swap-With-Parent) ili Dodaj do roditelja (eng. Move-To-Parent) algoritami. Druga klasa algoritama se koriste kada obrazac za pretraživanje pokazuje svojstvo koje se zove lokalnost veza, gde u datom vremenskom intervalu, samo za manji podskup liste je najviše verovatno da će se pristupiti. Ovo se takođe naziva i zavisnim pristupom jer verovatnoća pristupa određenom elementu zavisi od verovatnoće pristupa njegovim susednim elemenatima. Takvi modeli su uobičajeni u realnim aplikacijama kao što su baze podataka ili fajl sistemi i upravljanje memorijom i keširanje. Zajednički okvir za algoritame koji se bave takvim zavisnim okruženjima je da reorganizuje listu ne samo na osnovu evidencije pristupa za sam čvor, već i na evidenciji za čvorove blizu njega. To praktično podrazumeva reorganizaciju podliste liste na koju se evidencija odnosi.
Aplikacije koje koriste samoorganizovane liste[уреди | уреди извор]
Jezički prevodioci poput kompajlera i interpretatora koriste samoorganizovane liste za održavanje simbol-tabele tokom kompilacije ili interpretacije izvornog koda programa. Trenutno je u toku projekat koji bi trebao da uključi strukturu podataka samoorganizovane liste u sisteme da bi smanjile aktivnosti magistrala koje dovode do rasipanja snage u tim krugovima. Ove liste se takođe primenjuju u veštačkoj inteligenciji i neuronskim mrežama, kao i u samo-podešavajućim programaima. Algoritmi koji se koriste u samoorganizovanim listama se takođe koriste kao algoritmi za keširanje, kao na primer LFU algoritam.
Reference[уреди | уреди извор]
- ^ Knuth, Donald (1998), Sorting and Searching, The Art of Computer Programming, Volume 3 (Second ed.), Addison-Wesley. ISBN 978-0-201-89685-5. стр. 402..
- ^ http://www.springerlink.com/content/978-3-540-34597-8/#section=508698&page=1&locus=3[мртва веза] Lists on Lists: A Framework for Self Organizing-Lists in Environments with Locality of Reference
- Vlajic, N (2003), Self-Organizing Lists (PDF), Архивирано из оригинала (pdf) 06. 05. 2012. г., Приступљено 22. 03. 2014
- Self Organization (PDF), 2004, Архивирано из оригинала (pdf) 14. 04. 2012. г., Приступљено 22. 03. 2014
- NIST DADS entry
- A Drozdek, Data Structures and Algorithms in Java Third edition
- Amer, Abdelrehman; B. John Oommen (2006), Lists on Lists: A Framework for Self Organizing-Lists in Environments with Locality of Reference Lists on Lists: A Framework for Self-organizing Lists in Environments with Locality of Reference Проверите вредност параметра
|url=(помоћ) (pdf)[мртва веза]