Топологија (електрична кола)

С Википедије, слободне енциклопедије
За друге употребе, погледајте Топологија (вишезначна одредница).

Топологија електронског кола је форма изведена из мреже међусобних веза компоненти кола. Различите специфичне вредности или бројчани подаци о компнентама се сматрају да су иста топологија. Топологија се не бави физичким приказом компоненти у колу нити њиховом позицијом на дијаграму кола. Она се бави само везама које постоје између компоненти. Може постојати много физичких приказа и дијаграма кола који се сви своде на исту топологију. Строго узевши, замена компоненте компонентом потпуно другог типа је и даље иста топологија. У неким контекстима, међутим, ово се може мало слободније описати као различите топологије. На пример, замена индуктора кондензаторима у нископропусном филтеру доводи до високопропусног филтера. Ове топологије се могу описати као високопропусне и нископропусне топологије мада је топологија мреже идентична. Тачнији термин за ове класе објектата (тј. мреже где је тип компоненти спецификован али није апсолутна вредност) је прототип мреже. Топологија електронске мреже је повезана са математичком топологијом нарочито, јер мреже које садрже само двополарне уређаје имају топологију која се може сматрати применом теорије графова. У анализи мреже таквог кола са тополошке тачке гледишта чворови мреже су тачке у теорији графова, а гране мреже су гране у теорији графова. Стандардна теорија графова се може проширити да би обухватила активне компоненте и мултиполарне уређаје као што су интегрисана кола. Графови се могу користити у анализи бесконачних мрежа.

Дијаграми кола[уреди | уреди извор]

Дијаграми кола у овом тексту поштују уобичајене конвенције електронике; линије представљају проводнике, попуњени кружићи представљају спојеве проводника, празни кружићи представљају терминале за повезивање са спољашњим светом. У већини случајева импедансе су представљене правоугаоницима. Практични дијаграм кола би користио специфичне симболе за отпорнике, проводнике, кондензаторе итд, али топологија се не бави типовима компоненти у мрежи па се уместо тога користи симбол опште импедансе. У одељку о теорији графова у овом тексту дат је алтернативни метод за представљање мрежа.

Тополошка имена[уреди | уреди извор]

Многа тополошка имена се односе на њихов изглед када се нацртају у облику дијаграма. Већина кола се може нацртати на разне начине па зато имају различита имена. На пример, три кола приказана на Слици 1.1 сва изгледају различито али имају исте топологије.[1]

Figure 1.1. T,Y and Star topologies are all identical

Овај пример такође приказује уобичајена тополошка обележја по слову алфабета на које личи. Слова грчког алфабета се такође могу користити на овај начин П (пи) топологија и ∆ (делта) топологија.

Серијске и паралелне топологије[уреди | уреди извор]

За мрежу са две гране постоје само две могуће топологије: серијска и паралелна. : Серијска и паралелна кола.

Слика 1.2 серијске и паралелне топологије са две гране

Слика 1.2 серијске и паралелне топологије са две гране

Слика 1.3 све ове топологије су идентичне. Серијска топологија је општи назив. Напонски разделник или потенцијални разделник се користи за кола у ту сврху. Л-одељак је уобичајено име за тополгију у дизајну филтера.

а мрежу са три гране постоје четири могуће топологије:

Слика 1.4 серијске и паралелне топологије са три гране

Треба обратити пажњу на то да је паралелна /серијска топологија други начин представљања ∆ топологије о којој ће бити речи касније.

Серијске и паралелне топологије могу да прошире конструкцију све већим бројем грана до бесконачности. Број јединствених топологија које се могу добити из н грана је 2н-1. Укупан број јединствених топологија који се може добити са не више од н грана је 2н -1.

Y и ∆ топологије[уреди | уреди извор]

Slika 1.5 Y i ∆ topologije

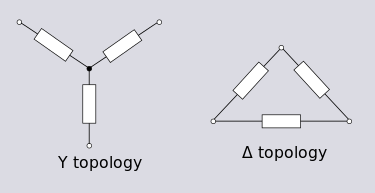
Y и ∆ су важне топологије у анализи линеарне мреже због тога што су оне најједноставније могуће трополне мреже. Y - ∆ трансформација је могућа за линеарна кола. Ова трансформација је важна зато што има неких мрежа које се не могу анализирати у смислу серијских и паралелних комбинација.

'Slika 1.6

Пример ове мреже је слика 1.6, која се састоји од Y мреже паралелно везане са ∆ мрежом. Рецимо да се тражи да се израчуна импеданса између два чвора мреже. У многим мрежама ово се може урадити само сукцесивном применом правила за комбиновање серијских и паралелних импеданси. У овом случају то није могуће јер је Y-∆ трансформација неопходна уз правила за серијске и паралелне импедансе.

Y топологија се зове још и топологија звезде. Међутим топологија звезде може да се односи и на општији случај са много грана повезаних за један чвор, више од три гране.



Топологија простих филтера[уреди | уреди извор]

Главни текст: топологија електронских филтера

Слика 1.7 уобичајене топологије балансираних и небалансираних филтера. Топологије приказане на слици 1.7 се најчешће користе за нацрте филтера и атенуатора. Л-одељак је тополошки идентичан топологији потенцијалног разделника. Т-одељак је идентичан топологији Y топологије. Π-одељак је идентичан топологије ∆ топологије. Све ове топологије могу се видети на сведеном пресеку лествичасте топологије. Дужи одељци би регуларно били описани као лествичаста топологија. Ове врсте кола су најчеће анализиране и описане као двоулазне мреже.

Топологија моста[уреди | уреди извор]

Главни текст: коло моста


Топологија моста је важна топологија са много употреба и у линеарним и у нелинеарним апликацијама укључујући међу осталима, исправљач моста, Витстонов мост и еквализатор фазе решетке. Постоји неколико начина на које се та топологија моста преноси на дијаграм кола. Први приказ је на слици 1.8 и то је традиционално приказивање кола моста. Други приказ јасно приказује еквивалентност између топологије моста и топологије изведене из серијских и паралелних комбинација. Трећи приказ је познатији као топологија решетке. Није баш очигледно да је то тополошки еквивалент. Може се видети да је то заиста тако визуализујући да се горњи леви чвор померио надесно до врха горњег десног чвора.


Слика 1.9. приказано је коло моста са аутпут улазом моста Уобичајено је звати мрежу моста топологијом само ако се користи као двоулазна мрежа са инпут и аутпут улазима од којих се сваки састоји од пара дијагонално супротних чворова. Топологија кутије на слици 1.7 може се сматрати топологијом моста али у случају филтера инпут и аутпут улази су по пар суседних чворова. Понекад унос (или нулти показатељ ) компоненте кроз аутпут улаз моста бива укључен у топологију моста приказан на слици 1.9.

Мост Т и дупло Т топологије[уреди | уреди извор]

Слика 1.10 мост Т топологија Мост Т топологија је изведена из топологије моста на начин објашњен у тексту о Зобеловој мрежи. Постоје многе изведене топологије које су описане у истом тексту. 

слика

Слика 1.11 Постоји такође дупло Т топологија која има практичну употребу тамо где је потребно да инпут и аутпут деле исти (базу) терминал. Ово се може десити, на пример, због тога што су инпут и аутпут повезани коаксијалном топологијом. Повезивање инпут и аутпут терминала није дозвољено код уобичајене тополгије моста и због тога дупло Т се користи где би се мост иначе био коришћен за равнотежу или примену нултог мерења. Топологија се често користи у дупло Т осцилаторима као генератор синусоиде. Доњи део слике 1.11 показује дупло Т топологију преправљену да би се истакла веза са топологијом моста.

Бесконачне топологије[уреди | уреди извор]

Лестивичаста топологија може се проширити безгранично и често се користи у дизајну филтера. Постоје многе варијације лествичасте топологије од којих су неке описане у текстовима о топологији електронског филтера и филтера композитне слике.

Слика 1.3 Антилествичаста топологија

Балансирани облик лестивчасте топологије може се видети као граф једне стране призме по произвољном реду. Страна антипризме прави топологију која је у том смислу антилестивичаста. Антилествичаста топологија проналази примену у колима са мултипликатором напона нарочито код Кокрофт-Волтоновог генератора. Постоји и пуноталасна верзија Кокрофт-Волтоновог генератора која користи дуплу антилествичасту топологију.

Бесконачне топологије могу се формирати и правећи каскаде од више одељака неких једноставнијих топологија као што су решетка или мост Т одељци. Такви бесконачни ланци одељака решетке појављују се у теоријским анализама и вештачким симулацијама преносних водова, али се ретко користе у практичној примени кола.

Компоненте са више од два терминала[уреди | уреди извор]

Кола која садрже компоненте са три или више терминала у великој мери повећавају број могућих топологија. Супротно томе број различитих кола представљен топологијом се смањује и у многим случајевима се лако разликује од топологије чак и када специфичне компоненте нису назначене.

Слика 1.4 топологија основног појачивача као што је обични емитерски биполарно спојни транзисторски појачивач Слика 1.5 балансирани појачивач као што је диференцијални појачивач

Теорија графова[уреди | уреди извор]

Теорија графова је област математике која се бави графовима. У анализи мреже графови се користе да би представили мрежу која се анализира. Граф мреже приказује само неке одређене аспекте мреже; ти аспекти се односе на њену спосбност повезивања или другим речима, на њену топологију. Ово може бити корисно представљање и генерализација мреже због тога што су многе једначине мреже непромењиве за све мреже са истом топологијом. Ово укључује једначине изведене из Кирхофових закона и Телегенове теореме.

Историја[уреди | уреди извор]

Теорија графова се користи у анализи мреже за линеарне пасивне мреже скоро од тренутка када су формулисани Кирхофови закони. Густаф Кирхоф лично је 1847. године, користио графове као апстрактну представу мреже у његовој анализи петље отпорног кола. Овај приступ је касније генерализован, довевши до РЛЦ кола, замењујући отпоре импедансама. Џејмс Клерк Максвел је 1892. године, дошао до дуала ове анализе, анлизом чворова. Максвел је такође одговаран за топологијску теорему да је детерминанта за матрицу адмитансе чвора једнака збиру производа све три адмитансе. Анри Поенкаре је 1900. године, увео представљање графа матрицом импедансе и тако засновао поље алгебарске топологије. Освалд Веблен је 1916. године, применио алгебарску топологију Поенкареа на Кирхофову анализу. Веблен је такође одговоран за увођење разапињућег стабла као помоћи при одабирању компатбилног скупа промењивих мреже.

Слика 2.1 дијаграм кола лестивчасте мреже нископропусног филтера: двоелементна врста мреже. Опсежни попис графова мреже како се примењују на електрична кола почеоје Перси МекМејхон, 1891. године (са чланком за инжињере у листу Електричар, 1892) који је ограничио свој елаборат на серијске и паралелне комбинације. МекМејхон је назвао ове графове спојни ланци. Роналд Фостер је 1932. године, категоризовао графове по њиховом проблему анулирања или рангу и дошао до карти свих оних са малим бројем чворова. Овај рад је настао на основу ранијег Фостеровог елабората док је сарађивао са Џорџом Кемпбелом 1920. године, на четвороулазном телефонском репетирору и произвео 83.539 различтих графова. Дуго је топологија у теорији електричних кола третирала самолинеарне пасивне мреже. Новији развој полупроводних уређаја и кола захтева нове алате у топологији да би их обрадила. Огроман пораст у комплексности кола довео је до комбинаторике у теорији графова да би се побољшала ефикасност рачунарских прорачуна.

Графови и дијаграми кола[уреди | уреди извор]

Слика 2.2 граф једне лествичасте мреже приказане на слици 2.1 са претпоставком да је лествица са четири пречке. Мреже се најчешће класификују по врсти електричних елемената који их сачињавају. На дијаграму кола ове врсте елемената се посебно цртају сваки са својим једиснтвеним симболом. Отпорничке мреже су једноелементне врсте мрежа које се састоје само од Р елемената. Тако су кондензаторске и индукционе мреже једноелементне мреже. РЦ, РЛ ЛЦ кола су једноставне двоелементне мреже. РЛЦ коло је најједноставнија врста троелементне мреже. ЛЦ лествичаста мрежа се најчешће користи за нископропусне филтере и може имати много елемената али је и још један пример двоелементне мреже. Супротно од тога топологија се бави само геометријским односима између елемената мреже а не врстама самих елемената. Средиште топологијске представе мреже је граф мреже. Елементи су представљени као гране графа. Грана се црта као линија која се завршава са тачкама или малим круговима из којих могу да пођу друге гране (елементи). У анализи кола гране графа се називају гранама. Тачке се називају тачкама графа и представљају чворове мреже. Чвор и тачка су термини који су међусобно замењиви када је реч о графовима мрежа. Слика 2.2 приказује представу графа кола са слике 2.1. Графови који се користе у анализи мреже су најчешће и усмерени графови да би се прибележио смер тока и напона струје, и означени графови да би се прибележила јединственост грана и чворова. На пример граф који се састоји од квадрата грана би и даље био тополошки исти граф ако би две гране биле међусобно замењене осим ако гране немају уникатне ознаке. У усмереним графовима два чвора које повезује грана су означена као изворни и циљни чвор. Најчеше ће стрелице нацртане на грани бити усмерене ка њима.

Инцидентност[уреди | уреди извор]

Главни текст: Матрица инцидентности Инцидентност је једна од основних особина графа. Грана која је повезана са тачком назива се инцидентном на тачку. Инцидентност графа може да се прикаже у форми матрице. Матрицом која се зове матрица инциденције. Заправо, матрица инциденције је алтернатива математичкој представи графа која уклања потребу за било каквим цртањем. Редови матрице одговарају чворовима а колоне матрице одговарају гранама. Елементи матирце су или нула ако нема инциденције или један ако постоји инциденција између чвора и гране. Смер усмереног графа је обележен знаком елемента.

Еквивалентност[уреди | уреди извор]

Графови су еквивалентни ако се један може трансформисати у други деформацијом. Деформација може укључивати операције транслације, ротације и рефлексије: савијање и истезање грана; и укрштање или учворавање грана. Два графа која су еквивалентна уз деформацију зову се конгруентним.

У пољу електричних мрежа постоје још две трансформације које доводе до еквивалентиних графова а не праве конгруентне графове. Прва од њих је замена места редно везаних грана. Ово је дуал замене места паралелно везаних грана који се може добити деформацијом без потребе за специјалним правилима. Друга је везана за графове који се деле на два или више одвојена дела то јест, граф са два сета чворова који немају гране инцидентне на чвор сваког сета. Два тако одвојена дела се сматрају еквивалентним графом са оним где су делови спојени комбиновањем чвора из сваког у један чвор. Такође граф који може да се подели на два одвојена дела дељењем чвора на два се такође сматра еквивалентним.

Стабла и везе[уреди | уреди извор]

Слика 2.3 једно могуће стабло графа са слике 2.2. везе су показане испрекиданим линијама Стабло је граф на којем су сви чворови повезани директно или индиректно гранама али без формирања било каквих затворених петљи. Пошто нема затворених петљи нема ни струје у стаблу. У анализи мреже интересују нас разапињућа стабла то јест, стабла која повезују сваки чвор присутан на графу мреже. У овом тексту разапињуће стабло се сматра потпуним стаблом осим ако није другачије наведено. Одређен граф мреже садржи неколико различитих стабала гране које се уклањају са графа да би се формирало стабло називају се везама, гране које остају на стаблу зову се гранчице. За граф са н чворова број грана на сваком стаблу т мора бити: формула Важан однос за анализу кола је: формула где је б број грана на графу а л број веза уклоњених да би се формирало стабло.

Спојни сетови и пресеци[уреди | уреди извор]

Циљ анализе кола је да одреди све струје и напоне гране у мрежи. Ове промењиве мреже нису све независне. Напон гране је повезан са струјама гране трансферном функцијом елемената од којих се састоји. Потпуно решење мреже, према томе, може бити или везано само за струје гране или само за напоне гране. Нису ни све струје гране независне једна од друге. Минимални број струја грана потребан да би се добило решење је л. Ово је последица чињенице да је са стабла уклоњено л веза и да не може бити струја у стаблу. Пошто преостале гране стабла имају нула струје оне не могу бити независне од струја везе. Струје гране које су изабране као сет независних промењивих морају бити повезане са везама стабла: не може се произвољно изабрати л грана. Што се тиче напона гране потпуно решење мреже може се добити уз т напона грана. Ово је последица чињенице да кратак спој свих грана стабла доводи до тога да је напон нула свуда. Напони везе не могу према томе бити независни од напона гране стабла.

Слика 2.4 пресек графа са слике 2.2 изведног са стабла са слике 2.3 избацивањем гране 3.

Уобичајен приступ анализе је да решава за струје петље пре него за струје гране. Струје гране се проналазе преко струје петље. Опет сет струја петље не може бити произвољно изабран. Да би се могао гарантовати сет независних промењивих струје петље морају бити оне које су повезане са одређеним сетом петљи. Овај сет петљи састоји се од оних петљи које су формиране замењивањем једне везе одређеног стабла графа анализираног кола. Пошто се замењивањем једне везе на стаблу формира тачно једна јединствена петља број струји петље тако добијен је једнак л. Термин петља нема исто значење као термин петље у теорији графа. Сет грана које формирају одређену петљу се зове спојни сет. Сет једначине мреже се формира изједначавањем струја петље са алгебарским збиром струја спојног сета грана. Могуће је изабрати сет независних струја петљи који се не односи на стабла и спојне сетове. Довољан, али не и неопходан услов за избор сета независних петљи је обезбеђивање да свака изабрана петља укључује бар једну грану која није претходно укључена у већ изабране петље. Нарочито једноставан избор је тај да се користи анализа подмреже у којој су све изабране петље подмреже. Анализа подмреже може да се примени само ако је могуће исцртати граф на раван или сферу без грана које се укрштају. Такви графови се зову планарни графови. Могућности исцртавања на раван или сферу су еквивалентни услови. Било који коначни граф исцртан на раван може бити смањен да би могао бити нацртан на мали регион сфере.

Обрнуто, подмрежа било ког графа исцртаног на сферу може се истегнути све док унутрашњи простор не покрије скоро целу сферу. Цео граф онда заузима само малу област сфере. Ово је исто као и у првом случају, према томе граф ће такође бити нацртан на раван. Постоји приступ избора промењивих мреже са напонима који је аналоган и дуалан методу струје петље. Овде напони повезани са паровима чворова су примарне промењиве и напони гране се изводе у том смислу. И у овом методу одређено стабло графа мора бити изабрано да би се осигурало да су све промењиве независне.


Дуал спојног сета је пресек. Спојни сет се формира дозвољавајући свим осим једне везе графа да буде отворено коло. Пресек се формира дозвољавајући свим осим једне гране стабла да буде кратак спој. Пресек се састоји од гране стабла која нема кратак спој и било која од веза које немају кратак спој због осталих грана стабла. Пресек графа даје два раздвојена подграфа тј он сече граф на два дела, и он је минимални сет грана потребних за то. Сет једначина мреже се формира изједначавањем напона пара чворова са алгебарским збиром пресека напона грана. Дуал посебног случаја анализе подмреже је анализа чвора.

Анулирање и ранг[уреди | уреди извор]

Анулирање Н неког графа са с одвојеним деловима и б гранама се дефинише;

Анулирање графа представља број степени слободе његовог сета једначина мреже. За планарни граф нулти број је једнак броју подмрежа у графу. Ранг Р графа је дефинисан; формула Ранг игра исту улогу у анализи чвора као анулирање у анализи подмреже. То да значи он даје број једначина напона чвора који је потребан.

Решавање промењивих мрежа[уреди | уреди извор]

Једном када се одабере сет геометријски независних промењивих стање мреже се изражава преко њих. Резултат је сет независних линеарних једначина које треба да се реше истовремено да би се нашле вредности промењивих мрежа. Овај сет једначина може бити изражен у форми матрице што води до карактеристичног параметра матрице за мрежу. Параметарске матрице узимају облик матрице импедансе ако су једначине формиране на основу анализе петље или као матрица адмитансе. Ако су једначине формиране на основу анализе чвора. Ове једначине се могу решавати на неколико познатих начина. Један метод је систематична елиминација промењивих. Други метод укључује употебу детерминанти. Ово је познато као Крамерово правило и пружа директан израз за непознате промењиве у форми детерминанти. Ово је корисно јер пружа компактан израз решења. Међутим, за било шта више од најтривијалнијих мрежа потребан је већи напор при израчунавању за овај метод када се ради ручно.

Дуалност[уреди | уреди извор]

Два графа су дуална кад је однос између грана и парова чвора у једном исти као и однос између грана и петљи у другом. Дуал графа може у потпуности бити изведен графичком методом. Дуал графа је такође граф. На одређеном стаблу графа комплементарни сет грана (тј гране које нису на стаблу) формирају стабло на дуалном графу. Сет једначине струје петље повезане са спојним сетовима оригиналног графа и стабло су идентични сету једначина напона пара чворова повезаних са пресеком дуалног графа. Следећа табела наводи концепте дуала у топологији везане за теорију кола.


Слика 2.5 Дуални граф графа на слици 2.2


Дуал стабла се понекад зове лавиринт. Он се састоји од поља повезаних везама на исти начин на који се стабло састоји од чворова повезаних гранама стабла.

Дуали се не могу формирати за сваки граф. Дуалност захтева да сваки спојни сет има дуални пресек на дуалном графу. Овај услов се испуњава само и једино ако граф може бити нацртан на сферу без укрштених грана. Да би се ово видело, обратите пажњу да се од спојног сета захтева да “раздвоји“ граф на два дела, а од његовог дуала, пресека се захтева да пресече граф на два дела. Граф коначне мреже који не може да се нацрта на сферу ће захтевати н-струки торус. Спојни сет који пролази кроз рупу у торусу неће успети да споји граф у два дела. Као последица тога дуални граф неће моћи да буде пресечен на два дела и неће садржати одговарајући пресек. Због тога само планарни графови имају дуале. Дуали такође не могу бити формирани за мреже које садрже међусобну индукцију пошто нема одговарајући кондензаторски елемент. Еквивалентна кола могу бити направљена а да немају дуале, али дуал не може бити направљен из међусобне индукције директно.

Елиминација чвора и подмреж[уреди | уреди извор]

Операције на сету једначина мреже имају тополошко значење које може помоћи визуелизацији онога што се догађа. Елиминација напона чвора из сета једначина мреже одговара тополошки елиминацији тог чвора из графа. За чвор који је повезан са три друга чвора то одговара добро познатој Y-∆ трансформацији. Трансформација може бити проширена на већи број повезаних чворова и онда је позната као трансформација подмреже у облику звезде.

Инверзија ове трансформације је трансформација ∆-Y што аналитички одговара елиминацији струје подмреже и тополошки одговара елиминацији подмреже. Међутим, елиминација струје подмреже где подмрежа има гране заједничке са произвољним бројем других подмрежа неће уопштено речено довести до изводљивог графа. Ово је због тога што је граф трансформација опште звезде граф који неће бити нацртан на сферу (он садржи полигон звезде и према томе вишеструко укрштање). Дуал таквог графа не може да постоји али је то граф неопходан да се представи уопштено елиминисање подмреже.

Међусобна спрега[уреди | уреди извор]

Слика 2.6 дупло подешено коло често се користи за фазу спреге резонантног појачивача. А, граф дупло подешеног кола. Б еквивалентни граф са раздвојеним комбинованим деловима. Нема начина да се експлицитно представи међусобна индуктивна спрега на конвенционалној графној представи кола, као што је то случај у трансфроматору, и такве компоненте могу довести до невезаног графа са више од једног одвојеног дела. За потребе анализе, граф са више делова може се комбиновати у један граф сједињавањем једног чвора из сваког дела у јединствен чвор. Ово не представља разлику у теоретском понашању кола, па је анализа изведена из тога и даље валидна. Међутим, у пракси би постојала разлика јер би коло употребљено на овај начин уништило изолацију између делова. Пример би био трансформатор уземљен и на примарној и на секундарној страни. Трансформатор и даље функционише као трансфроматор са истим опсегом напона али сада не може више да буде коришћен као трансформатор изолације.

Новије технике у теорији графа могу да се баве активним компонентама које су такође проблематичне у конвеницоналној теорији. Ове нове технике такође могу да се баве међусобном спрегом.

Активне компоненте[уреди | уреди извор]

Постоје два основна прилаза доступна за рад на међусобној спрези и активним компонентама. У првом од њих, Семјуел Џеферсон Мејсон је 1953. године, увео графове тока сигнала. Графови тока сигнала су тежински, усмерени графови. Он их је користио да анализира кола која садрже међусобну спрегу и активне мреже. Тежина усмерене гране на овим графовима представља појачање исто као код појачивача. Уопштено, графови тока сигнала за разлику од уобичајених усмерених графова описаних горе не одговарају тополгији физичког распореда компоненти. Други приступ је да се прошири класичан метод тако да укључује међусобне спреге и активне компоненте. Неколико метода је предложено да би се то постигло. У једном од њих два графа се конструишу, један представља струје у колу а други представља напоне. Пасивне компоненте ће имати идентичне гране на оба стабла али активне компоненте можда неће. Метод се ослања на проналажење разапињућих стабала која су заједничка за оба графа. Алтернативни метод је проширење класичног приступа што захтева само један граф и био је предложен од стране Чена 1965. Ченов метод се заснива на коренском стаблу.

Хиперграфови[уреди | уреди извор]

Други начин проширење класичне теорије графа за активне компоненте је кроз употребу хиперграфова. Неке електронске компоненте нису представљене у регуларној употреби графова. Транзистор има три конекционе тачке, али нормална грана графа може да повеже само два чвора. Модерна интегрисана кола имају много више веза. Овај проблем може да се превазиђе коришћењем хиперграфова уместо обичних графова.


Слика 2.7 пример хиперграфа. Уобичајене гране су приказане црном бојом, хипер гране су приказане плавом, а пипци су приказани црвеном. У конвенционалном представљању компоненте су приказане гранама, од којих свака спаја два чвора. На хиперграфу компоненте су приказане хипергранама које могу да спајају произвољан број чворова. Хипергране имају пипке који повезују хипгране са чворовима. Графички приказ хипергране може бити кутија (у поређењу са граном која је линија) а приказ њених пипака су линије од кутије до повезаних чворова. На усмереном хиперграфу пипци имају ознаке одређене ознаком хипергране. Конвенционални усмерени граф може се сматрати хиперграфом са хипергранама од које свака има два пипка. Ова два пипка су обележена као извор и циљ и најчешће на њих указује стрелица. За уопштени хиперграф са више пипака потребно је комплексније обележавање. Хиперграфови могу бити описани њиховим матрицама инциденције. Уобичајени граф који садржи само двополарне компоненте имаће само тачно два уноса у сваки ред матрице који нису нула. Било која матрица инциденције са више од два уноса који нису нула у било ком реду представља хиперграф. Број уноса који нису нула у реду је ранг одговарајуће гране а највиши ранг гране је ранг матрице инциденције.

Нехомогене промењиве[уреди | уреди извор]

Класична анализа мреже развија сет једначина мреже чије су промењиве мреже хомогене за сваку струју (анализа петље) или напон (анализа чвора). Сет промењивих мреже тако добијен није неопходно минимум неопходан да се добије сет независних једначина. Може постојати разлика између броја промењивих у анализи петље и анализи чвора. У неким случајевима најмањи могући број може бити мањи од било ког од ових бројева, ако је услов хомогености флексибилан и ако је дозвољено мешање промењивих струја и напона. Резултат Кишија и Катађинија из 1967, је да се апсолутни минимални број промењивих неопходан да се опише понашање мреже изводи из максималне раздаљине између било које две разапињуће шуме графа мреже.

Синтеза мреже[уреди | уреди извор]

Теорија графа може бити примењена на синтезу мреже. Класична синтеза мреже реализује потребну мрежу у једној од неколико утвђених форми. Примери утврђених форми су реализација покретача импедансе по Кауеровој лествичавој мрежи или Фостеровој утврђеној форми или Бруновој реализацији имитанце из његових позитивно-реалних функција. Тополошки методи с друге стране, не крећу од дате утврђене форме. Код њих форма је пре резултат математичког представљања. Неке утврђене форме захтевају међусобну индукцију да би се реализовале. Велики циљ тополошких метода синтезе мреже је да елиминише потребу за овим међусобним индукцијама. Једна теорема проистекла из топологије је да реализација покретања импедансе без међусобне спреге буде минимална ако и само ако не постоје петље које се састоје само од индуктора или само од кондензатора. Теорија графа је најснажнија у синтези мреже када елементи мреже могу бити представљени реалним бројевима (једноелементне врсте мрежа као што су отпорничке мреже) или бинарним изразима (као што су прекидачке мреже).

Бесконачне мреже[уреди | уреди извор]

Можда је најстарија мрежа са бесконачним графом која је проучавана била лествичаста мрежа коришћена да се представе развијене трансмисионе линије у њеној коначној форми од стране Оливера Хевисајда 1881. Сигурно су рана проучавања бесконачних мрежа била ограничена на периодичне структуре као што су лестивце или решетке са истим елементима који се непрестано понављају. Тек крајем двадесетог века алати за анализирање бесконачних мрежа са произвољном топологијом су постали доступни. Бесконачне мреже су углавном ствар теоријског инетересовања и играчке су математичара. Бесконачне мреже које нису ограничене границама стварног света могу да имају нека нефизичка својства.

На пример, Кирхофови закони могу да оману у неким случајевима и бесконачне лествице отпорника се могу одредити покретањем импедансе које зависи од терминације у бесконачности. Још једно нефизичко својство теоретски бесконачних мрежа је да уопштено оне расипају бесконачну енергију осим ако се на њих не ставе стеге уз додатне уобичајене законе мреже као што су Омови и Кирхофови закони. Међутим, постоје и неке примене у стварном свету. Пример трансмисионе линије је један из класе практичних проблема који може бити обликован од стране инфинитезималних елемената (модел расутих елемената). Други примери су покретање таласа у континуираном медијуму, проблеми ивичног поља и мерења отпора између тачака подлоге или продубљивање. Трансфинтитне мреже проширују идеју бесконачних мрежа још више. Чвор на крајњем делу бесконачне мреже може да има још једну грану с њим повезану која води до следеће мреже. Ова следећа мрежа може и сама да буде бесконачна. Према томе топологије могу бити конструисане тако да имају пар чворова без коначних путева између њих. Такве мреже бесконачних мрежа се зову трансфинитне мреже.

Нотација[уреди | уреди извор]

1 иди на ̂ Спојни ланац. Терминологија састављена од стране Артура Кејлија. Спојеви су гране у паралелној вези, ланци су гране у серијској вези (МекМејхон 1891, стр 330). Посебна грана се може сматрати или спојем или ланцем.

2 иди на ̂ Спојни сет. Термин спојни сет је осмислио Ернст Гиљемин (Гиљемин, стр xв). Гиљемин каже да је име изабрано зато што ако се гране спојног сета смање на нулту дужину граф би постао “развезан“ као рибарска мрежа са потезном петљом (Гиљемин, стр 17). Гиљемин је био водећа фигура у развоју и подучавању о анализи линеарне мреже (Вајлдс и Линдгрен, стр 154-159).

3 иди на ̂ Подмрежа. Подмрежа је петља која не обухвата било коју другу петљу.

4 иди на ̂ Лавиринт. Овај термин је још једна кованица од стране Гиљемина (Гиљемин, стр xв). Тако је назван због тога што поља на графу бивају пресецана везама и изгледају као лавиринт.

5 иди на ̂ Чен, Ваи-Каи, “Тополошка анализа за активне мреже“, ИЕЕЕ Трансакција теорије кола, вол 13, четврто издање, стр 438-439, децембар, 1966. 6 иди на ̂ кратак садржај овог дела је прво презентован у: Киши, Гења; Кађитани, Јоџи “ О максимално израженим стаблима“, Пета годишња Алертон конференција о теорији кола и система, стр 635-643, 1967. Погледај део библиографије где се налази цео рад објављен касније 1969. 7 иди на ̂ Размак између стабала се дефинише као број грана које су на једном стаблу али нису на другом. Тј. то је број грана који се мора променити да би се једно стабло трансформисало у друго (Киши и Кађитани, стр 323) 8 иди на ̂ Разапињуће шуме. Шума стабала у којој је сваки чвор графа у контакту са једним од стабала.

Референце[уреди | уреди извор]

  1. ^ Guillemin 1953, стр. 5–6.

Литература[уреди | уреди извор]

Преузето из „https://sr.wikipedia.org/w/index.php?title=Топологија_(електрична_кола)&oldid=27431314”