Бинарни хип

Бинарни хип (енгл. binary heap) је хип структура података организована по принципу бинарног стабла. Може се посматрати као бинарно стабло са два додатна ограничења:

Својство облика: Стабло је комплетно бинарно стабло ако сви нивои стабла, осим можда последњег, у потпуности попуњени, а у случају да последњи ниво стабла није попуњен, чворови тог нивоа се попуњавају с лева на десно.
Својство хипа: Сви чворови су или “већи или једнаки” или “мањи или једнаки” од сваког чвора који му је дете у зависности од тога која функција за поређење се користи у имплементацији.

Стабло са функцијом за поређење “веће или једнако” (≥) се зове маx-хеап, а са функцијом за поређење “мање или једнако” (≤) се зове мин-хеап. Мин-хеап се користи за примену редова са приоритетом. ^[1]^[2]

Пошто ред рођака у хипу није спецификован својствима хипа, два детета једног чвора могу бити слободно замењена, осим ако то не нарушава својство облика.

Бинарни хип је посебан пример н-арног хипа где је н=2.

Операције у хипу[уреди | уреди извор]

I операција уметања и операција уклањања модификују хип тако да се прво задовољи својство облика додавањем или уклањањем чвора са дна стабла, а затим се реализује својство хипа попречним кретањем по хипу. I једна и друга операција захтевају временску сложеност О(лог н).

Уметање[уреди | уреди извор]

Да би се елемент додао у стабло морамо обавити уп-хеап операцију (такође: буббле-уп, перцолате-уп, сифт-уп, трицкле-уп, цасцаде-уп) пратећи следећи алгоритам:

Додај елемент у доњи ниво стабла
Упореди додати елемент са његовим родитељем; ако су у исправном редоследу стани
Ако не, замени убачени елемент са његовим родитељем и врати се на претходни корак.

Број потребних операција зависи од броја нивоа које нови елемент мора да пређе да би задовољио својство хипа па зато операција уметања има временску сложеност О(лог н). Међутим, 1974.године [Томас Портер] и [Истван Сајмон] доказали су да функција за просечан број нивоа које један убачен цвор пређе има горњу границу - константу 1.6067.^{[тражи се извор]} Просечан број потребних операција за уметање у бинарно стабло је 2.6067 јер је обављено једно додатно поређење које не резултује померањем убаченог чвора за један ниво нагоре. Стога, у просеку, уметање у бинарно стабло има константну временску сложеност, О(1). Ово има смисла јер приближно 50% елемената чини лишће стабла, а приближно 75% елемената се налази на доња два нивоа. Врло је вероватно да ће се подаци које треба убацити помаћи за неколико нивоа нагоре да би се стабло одржало.

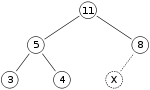
Као пример уметања података у бинарно стабло узећемо маx-хеап:

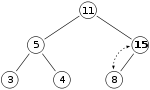
Ако желимо да убацимо број 15 у стабло, треба прво да поставимо број на место које означава X. Међутим, особина стабла је нарушена јер је 15 веће од 8, тако да треба да им заменимо места. Добијамо стабло које, након прве замене, изгледа овако:

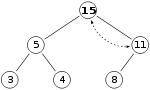
Особина стабла је и даље нарушена јер је 15 веће од 11, тако да је потребна још једна замена:

Добијамо исправно маx-хеап стабло. Након овога, нема потребе да проверавамо децу. Пре него што смо поставили 15 на означено место, стабло је било исправно, односно 11 је веће од 5. Ако је 15 веће од 11, а 11 веће од 5, онда и 15 мора бити веће од 5 због принципа прелазности.

Брисање[уреди | уреди извор]

Поступак брисања корена из хипа (ефикасно уклањање максималне вредности када је у питању маx-хеап или минималне када је у питању мин-хеап) и обнављање особина се зове доwн-хеап (такође: буббле-доwн, перцолате-доwн, сифт-доwн, хеапифy-доwн, еxтрацт-мин/маx). То се ради по следе'ем алгоритму:

Замени корен хипа последњим елементом на последњем нивоу
Упореди нови корен са његовом децом; ако су у правилном поретку стани
Ако не, замени елемент са једним од његове деце и врати се на претходни корак. (Замени најмањим дететом за мин-хеап и највећим за маx-хеап)

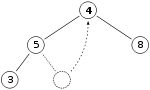
Затим, уколико имамо исти маx-хеап као и пре

Уклањамо 11 и постављамо 4.

Сада је особина стабла нарушена јер је 8 веће од 4. У овом случају, замена ова два елемента, 4 и 8, биће довољна да врати својство стабла тако да је додатна замена непотребна.

Унос који се кретао према доле мењан је већим међу децом за маx-хеап (за мин-хеап био би замењен најмањим дететом), све док његова нова позиција није испунила услов нормалног поретка у хипу. Ова функционалност постигнута је Маx-Хеапифy функцијом као што је доле дефинисано у псеудокоду за хип засновано на низу А дужине: хеап_ленгтх[А]. Приметићете да је “А” индексирано од 1, а не од 0 као што је чест случај код многих стварних програмских језика.

Маx-Хеапифy^[3] (А, и):

  left ← 2i
  right ← 2i + 1
  largest ← i
  if left ≤ heap_length[A] and A[left] > A[largest] then:
     largest ← left
  if right ≤ heap_length[A] and A[right] > A[largest] then:
     largest ← right
  if largest ≠ i then:
    swap A[i] ↔ A[largest]
    Max-Heapify(A, largest)

Да би овај алгоритам исправно преуредио низ, цвор са индексом и и његова директна два детета морају да наруше својство хипа. Уколико не наруше својство хипа, алгоритам ће бити спроведен без икаквих промена у низу. Операција доwн-хеап (без претходне замене) може такође бити употребљена да би се модификовала вредност корена, чак и ако елемент није избрисан. У најгорем случају, нови корен мора бити замењен својим дететом на сваком нивоу све док не спадне на доњи ниво хипа, што значи да операција брисања има временску сложеност која је повезана са висином стабла, или О(лог н).

Изградња стабла[уреди | уреди извор]

Хип може бити изграђен узастопним убацивањем. Овај приступ захтева $O(n\log n)$ времена јер сваки унос захтева $O(\log n)$ времена, а постоји н елемената. Међутим, ово није оптимални метод. Оптимални метод почиње произвољним додавањем елемената у бинарно стабло, пратећи својство облика (стабло може бити представљено као низ). Затим, крећући од најнижег нивоа према вишим, заменити корен сваког подстабла према доле као у алгоритму за брисање све док се својство хипа не обнови. Тачније, ако је свако подстабло које се налази на истој висини $h$ (мерено са дна) већ нагомилано (енгл. heapified), онда стабла на висини $h+1$ могу бити нагомилана (енгл. heapify) померањем корена према доле пратећи путању деце са највећим вредностима као када се прави маx-хеап или путању деце минималних вредности ако је у питању мин-хеап. Овај процес захтева $O(h)$ операција (замена) по чвору. У овом методу највише гомилања (енгл. heapification) се одвија на нижим нивоима. Пошто је висина хипа $\left\lfloor \lg(n)\right\rfloor$ , број чворова на висини $h$ је $\leq \left\lceil 2^{\left(\lg n-h\right)-1}\right\rceil =\left\lceil {\frac {2^{\lg n}}{2^{h+1}}}\right\rceil =\left\lceil {\frac {n}{2^{h+1}}}\right\rceil$ . Стога, цена гомилања свих подстабала је:

{\begin{aligned}\sum _{h=0}^{\lceil \lg n\rceil }{\frac {n}{2^{h+1}}}O(h)&=O\left(n\sum _{h=0}^{\lceil \lg n\rceil }{\frac {h}{2^{h+1}}}\right)\\&\leq O\left(n\sum _{h=0}^{\infty }{\frac {h}{2^{h}}}\right)\\&=O(n)\end{aligned}}

Ово користи чињеницу да задати бесконачни низ х / 2^х има граничну вредност 2. Тачна вредност ове једначине (највећи могући број поређења током изградње хипа) једнак је:

2n-2s_{2}(n)-e_{2}(n)

,^[4]

где ₂(н) представља збир свих цифара н бинарног система, а е₂(н) представља експонент 2 у основном разлагању на просте чиниоце.

Функција Буилд-Маx-Хеап која следи, претвара низ А у којем је сачувано комплетно бинарно стабло са н цворова у маx-хеап тако што изнова користи Маx-Хеапифy функцију по принципу од дна ка врху. Ово је засновано на закључку да је сваки елемент низа индексиран са флоор(н/2) + 1, флоор(н/2) + 2, ..., н представља лишће једног стабла, тако да сваки представља хип са само једним елементом. Буилд-Маx-Хеап спроводи Маx-Хеапифy на сваком од преосталих чворова стабла.

Буилд-Маx-Хеап^[3] (А):

  heap_length[A] ← length[A]

  for i ← floor(length[A]/2) downto 1 do

    Max-Heapify(A, i)

Имплементација хипа[уреди | уреди извор]

Хипови се углавном имплементирају заједно са низом. Свако бинарно стабло може бити сачувано преко низа, али пошто је бинарни хип скоро увек комплетно бинарно стабло, оно може бити сачувано и компактно. Показивачи нису потребни. Уместо тога, родитељ и деца сваког цвора могу бити пронађени путем аритметике у индексима низа. Ове карактеристике чине овакву примену стабла једноставним примером једне имплицитне структуре података или Ахнентафел листу. Детаљи зависе од позиције корена, а корен може да зависи од ограничења програмског језика коришћеног за имплементацију или од програмеровог избора. Понекад је корен постављен са индексом 1, жртвујући на тај начин простор само да би се поједноставила аритметика. Операција пеек за проналажење минималних/максималних вредности једноставно враћа вредност корена, те стога износи О(1).

Нека је н број елемената у стаблу а и произвољни исправни индекс низа по коме је стабло сачувано. Уколико је корен стабла индекс 0, са исправним индексима 0 до н – 1, онда сваки елемент а са индексом и има

Децу са индексом 2и + 1 и 2и + 2
Њихове родитеље ⌊(и − 1) ∕ 2⌋ где је ⌊…⌋ флоор функција која мапира реалан број до највећег претходног или најмањег следећег целог броја.

У другом случају, када је корен стабла на индексу 1 са исправним индексима 1 до н, онда сваки елемент а са индексом и има:

Децу са индексима 2и и 2и +1
Њихове родитеље са индексом ⌊и ∕ 2⌋.

Ова имплементација се користи код хипсорт алгоритма за сортирање где је дозвољено да се простор у улазни низ поново искористи за чување хипа. Алгоритам врши сортирање у месту). Имплементација је такође корисна као и ред са приоритетом где коришћење динамичког низа дозвољава убацивање неограниченог броја чланова.

Операције упхеап/доwнхеап могу бити изражене по принципу низа на следећи начин: претпоставимо да особина хипа задржава индексе б, б+1, …, е. Функција сифт-доwн проширује особину хипа на б-1, б, б+1, …, е. Само индекс и = б-1 може да наруши карактеристике хипа. Нека је ј индекс највећег детета а[и] за маx-хеап, или најмањег детета за мин-хеап у распону од б ,…, е. Ако не постоји такав индекс јер је 2и > е онда се карактеристике хипа чувају и за нови ниво и нема потребе да се било шта мења. Мењањем вредности а[и] за а[ј] карактеристике за позицију и су утврђене. У овом тренутку, једини проблем је то што карактеристика хипа можда неће сачувати индекс ј. Функција сифт-доwн се примењује реп-рекурзивно на индекс ј све док карактеристике хипа не постану исправне за све елементе.

Функција сифт-доwн је брза. У сваком кораку обавља два поређења и једну замену. Индексна вредност о којој се ради се дуплира сваким понављањем тако да је највише лог₂ е корака потребно.

За велике хипове и за коришћење виртуелне меморије, чување елемената у низу пратећи претходну шему није ефикасно: скоро сваки ниво се налази на другој страни. Б-хеап Б-хеап је бинарни хип који чува сва подстабла на једној страни, тако да је за десет пута мањи број страна којима се приступа.^[5]

Операција спајања два бинарна хипа захтева Θ(н) времена у случају изједначених хипова. Најбоље што можете да урадите (за случај примене низа) је да једноставно спојите два хипа са низом и добијете стабло које сте тражили.^[6] Хип са н елементима може бити спојен са хипом од к елементима коришћењем О(лог н лог к) поређења, или у случају имплементације засноване на показивачима за О(лог н лог к) времена.^[7] Алгоритам за раздвајање једног хипа са н елемената на два хипа са к и н-к елемената, заснован је на прављењу колекције подхипова.^[8] Тај алгоритам захтева О(лог н * лог н) поређења. За спајање хипова се користи концептуално једноставан алгоритам. Када је спајање учестали задатак, препоручује се другачији начин имплементације стабла, као што је биномијални хеап, који може бити спојен за О(лог н). времена.

Бинарни хип може бити имплементиран у складу са традиционалним начином чувања података, али ту постоји проблем са проналажењем суседних елемената на последњем нивоу бинарног хипа приликом додавања новог елемента. Овај елемент може бити одређен алгоритмички или убацивањем додатних података у чворове, који се зову везом дрвета - уместо чувања референци на децу, чувамо инордер наследнике чвора.

Могуће је модификовати структуру хипа тако да дозвољава издвајање и највећих и најмањих елемената за $O$ $(\log n)$ времена.^[9]. Да би се то постигло, редови се наизменично пребацују између минималног и максималног хипа. Алгоритми су наизглед исти, осим што се при сваком кораку морају узети у обзир наизменични редови са наизменичним поређењима. Спровођење је скоро исто као и код нормалног хипа са једним правцем. Ова идеја може се уопштити за мин-маx-медиан хип.

Извођење индексне једначине[уреди | уреди извор]

У хипу са низом, деца и родитељи чворова могу бити лоцирани извођењем једначина са индексом чвора. Овај део изводи битне једначине за хип са кореном који има индекс 0, са додатним напоменама за хип са кореном који има индекс 1. Да бисмо избегли забуне, дефинисаћемо ниво чвора као његову удаљеност од корена, тако да сам корен заузима ниво 0.

Чворови деце[уреди | уреди извор]

За општи чвор лоциран на индексу (почевши од 0), прво ћемо извести индекс десног детета, ${\text{right}}=2i+2$ . Нека је чвор $i$ лоциран на нивоу $L$ , с тим да сваки ниво $l$ садржи тачно $2^{l}$ чворова. Затим, постоји тачно $2^{l+1}-1$ чворова садржаних у слојевима укључујући и слој $l$ (размислите о бинарном рачунању: 0111...111 = 1000...000 – 1 ). Пошто је корен позициониран на нулу, $k$ -ти цвор ће бити смештен на индекс $(k-1)$ . Сви ови закључци доводе до следеће једначине за индекс последњег чвора на слоју л.

{\text{last}}(l)=(2^{l+1}-1)-1=2^{l+1}-2

Узмимо $j$ -ти чвор након чвора $i$ на слоју L, тако да је

{\begin{alignedat}{2}i=&\quad {\text{last}}(L)-j\\=&\quad (2^{L+1}-2)-j\\\end{alignedat}}

Сваки од ових $j$ -тих чворова мора имати тачно 2 детета, тако да треба да постоји $2j$ чворова који одвајају десно дете чвора $i$ од краја његовог слоја ( $L+1$ )

{\begin{alignedat}{2}{\text{right}}=&\quad {\text{last(L + 1)}}-2j\\=&\quad (2^{L+2}-2)-2j\\=&\quad 2(2^{L+1}-2-j)+2\\=&\quad 2i+2\end{alignedat}}

као што је захтевано.

Ако приметимо да је лево дете било ког чвора увек једну позицију испред десног детета неког од тих чворова, добићемо ${\text{left}}=2i+1$ .

Ако је корен лоциран на индексу 1 уместо на 0, последњи чвор сваког нивоа је услед тога на индексу $2^{l+1}-1$ . Користећи ово све до краја добијамо ${\text{left}}=2i$ и ${\text{right}}=2i+1$ за хип са кореном на индексу 1.

Чворови родитеља[уреди | уреди извор]

Сваки чвор је или лево или десно дете истог родитеља, тако знамо да ли је следећа једначина тачна или не:

$i=2\times ({\text{parent}})+1$
$i=2\times ({\text{parent}})+2$

Зато је

{\text{parent}}={\frac {i-1}{2}}{\textbf {or}}{\frac {i-2}{2}}

Сада размотримо израз $\left\lfloor {\dfrac {i-1}{2}}\right\rfloor$ .

Ако је чвор и лево дете, добијамо резултат истог тренутка, међутим, тачан резултат добијамо и ако је чвор и десно дете. У овом случају, $(i-2)$ мора бити паран, а самим тим $(i-1)$ мора бити непаран.

{\begin{alignedat}{2}\left\lfloor {\dfrac {i-1}{2}}\right\rfloor =&\quad \left\lfloor {\dfrac {i-2}{2}}+{\dfrac {1}{2}}\right\rfloor \\=&\quad {\frac {i-2}{2}}\\=&\quad {\text{parent}}\end{alignedat}}

Стога, без обзира на то да ли је чвор лево или десно дете, његов родитељ може бити пронађен путем једначине:

{\text{parent}}=\left\lfloor {\dfrac {i-1}{2}}\right\rfloor

Референце[уреди | уреди извор]

^ „хеапq – Хеап qуеуе алгоритхм”. Пyтхон Стандард Либрарy.
^ „Цласс ПриоритyQуеуе”. Јава™ Платформ Стандард Ед. 6.
^ ^а ^б Цормен, Т. Х.; ал. (2001), Интродуцтион то Алгоритхмс (2нд изд.), Цамбридге, Массацхусеттс: Тхе МИТ Пресс, ИСБН 978-0-07-013151-4 Непознати параметар |наме-лист-стyле= игнорисан (помоћ)
^ Суцхенек, Марек А. (2012), „Елементарy Yет Прецисе Wорст-Цасе Аналyсис оф Флоyд'с Хеап-Цонструцтион Програм”, Фундамента Информатицае, ИОС Пресс, 120 (1): 75—92, дои:10.3233/ФИ-2012-751
^ Поул-Хеннинг Камп. "Yоу'ре Доинг Ит Wронг". АЦМ Qуеуе. Јуне 11, 2010.
^ Цхрис L. Кусзмаул. "бинарy хеап" Архивирано на сајту Wayback Machine (8. август 2008). Dictionary of Algorithms and Data Structures, Paul E. Black, ed., U.S. National Institute of Standards and Technology. 16 November 2009.
^ J.-R. Sack and T. Strothotte "An Algorithm for Merging Heaps"^{[мртва веза]}, Acta Informatica 22, 171-186 (1985).
^ . J.-R. Sack and T. Strothotte "A characterization of heaps and its applications" Information and Computation Volume 86, Issue 1, May 1990, Pages 69–86.
^ Atkinson, M.D., J.-R. Sack, N. Santoro, and T. Strothotte (1. 10. 1986). „Min-max heaps and generalized priority queues.” (PDF). Programming techniques and Data structures. Comm. ACM, 29(10): 996–1000. Архивирано из оригинала (PDF) 27. 01. 2007. г. Приступљено 30. 03. 2014.

[1] „хеапq – Хеап qуеуе алгоритхм”. Пyтхон Стандард Либрарy.

[2] „Цласс ПриоритyQуеуе”. Јава™ Платформ Стандард Ед. 6.

[CLRS-3] а ^б Цормен, Т. Х.; ал. (2001), Интродуцтион то Алгоритхмс (2нд изд.), Цамбридге, Массацхусеттс: Тхе МИТ Пресс, ИСБН 978-0-07-013151-4 Непознати параметар |наме-лист-стyле= игнорисан (помоћ)

[4] Суцхенек, Марек А. (2012), „Елементарy Yет Прецисе Wорст-Цасе Аналyсис оф Флоyд'с Хеап-Цонструцтион Програм”, Фундамента Информатицае, ИОС Пресс, 120 (1): 75—92, дои:10.3233/ФИ-2012-751

[5] Поул-Хеннинг Камп. "Yоу'ре Доинг Ит Wронг". АЦМ Qуеуе. Јуне 11, 2010.

[6] Цхрис L. Кусзмаул. "бинарy хеап" Архивирано на сајту Wayback Machine (8. август 2008). Dictionary of Algorithms and Data Structures, Paul E. Black, ed., U.S. National Institute of Standards and Technology. 16 November 2009.

[7] J.-R. Sack and T. Strothotte "An Algorithm for Merging Heaps"^{[мртва веза]}, Acta Informatica 22, 171-186 (1985).

[8] . J.-R. Sack and T. Strothotte "A characterization of heaps and its applications" Information and Computation Volume 86, Issue 1, May 1990, Pages 69–86.

[sym-9] Atkinson, M.D., J.-R. Sack, N. Santoro, and T. Strothotte (1. 10. 1986). „Min-max heaps and generalized priority queues.” (PDF). Programming techniques and Data structures. Comm. ACM, 29(10): 996–1000. Архивирано из оригинала (PDF) 27. 01. 2007. г. Приступљено 30. 03. 2014.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]