Binarni sistem

S Vikipedije, slobodne enciklopedije

Binarni sistem je brojčani sistem u kome se zapis sastoji samo od cifara 0 i 1. Ovo je pozicioni brojčani sistem, sa osnovom 2. Svaki broj se može predstaviti kao zbir eksponenata dvojke. Zbog jednostavnosti primene u elektronskim kolima, binarni sistem koriste praktično svi moderni računari.

Koncept binarnog sistema omogućen je tek sa uvođenjem koncepta nule u sistemu arapskih cifara.

Primer binarnog zapisa: 1012 = 1·22 + 0·21 + 1·20, 101 u binarnom sistemu je ekvivalent broju 5 u dekadnom sistemu.

Istorija[uredi | uredi izvor]

Egipat[uredi | uredi izvor]

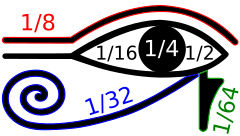
Vidi još: Staroegipatska matematika
Aritmetičke vrednosti za koje se smatra da su predstavljene delovima Horusovog oka

Pisci starog Egipta koristili su dva različita sistema za svoje razlomke, egipatske razlomke (koji nisu povezani sa binarnim brojevnim sistemom) i razlomke Horusovog oka (tako nazvane jer mnogi istoričari matematike veruju da bi simboli koji se koriste za ovaj sistem mogli biti raspoređeni tako da formiraju oko Horusa, iako je to sporno).[1] Razlomci Horusovog oka su binarni sistem numerisanja za razlomke količine zrna, tečnosti ili drugih mera, u kojima se razlomak hekata izražava kao zbir binarnih razlomaka 1/2, 1/4, 1/8, 1 /16, 1/32 i 1/64. Rani oblici ovog sistema mogu se naći u dokumentima iz Pete egipatske dinastije, otprilike 2400. godine pre nove ere, a njegova potpuno razvijena hijeroglifska forma datira iz Devetnaeste dinastije Egipta, otprilike 1200. godine p. n. e.[2]

Metoda korišćena za staroegipatsko množenje je takođe blisko povezana sa binarnim brojevima. U ovoj metodi, množenje jednog broja sa sekundom se izvodi nizom koraka u kojima se vrednost (u početku prvi od dva broja) ili udvostručuje ili joj se vraća prvi broj; redosled kojim se ovi koraci trebaju izvršiti je dat binarnim prikazom drugog broja. Ovaj metod se može videti u upotrebi, na primer, u Rajndovom matematičkom papirusu, koji datira od oko 1650. godine p. n. e.[3]

Kina[uredi | uredi izvor]

Daoistička Bagua

Ji đing datira iz 9. veka p. n. e. u Kini.[4] Binarni zapis u Ji đingu se koristi za tumačenje njegove tehnike kvartarnog proricanja.[5]

To je bilo zasnovano na taoističkoj dualnosti jina i janga.[6] Osam trigrama (Bagua) i skup od 64 heksagrama („šezdeset četiri“ gua), analogni trobitnim i šestobitnim binarnim brojevima, bili su u upotrebi barem još u dinastiji Džou u drevnoj Kini.[4]

Naučnik iz dinastije Song Šao Jong (1011–1077) preuredio je heksagrame u format koji podseća na moderne binarne brojeve, iako nije nameravao da se njegov raspored koristi matematički.[5] Gledanje najmanje značajnog bita na vrhu pojedinačnih heksagrama u Šao Jongovom kvadratu[7] i čitanje duž redova bilo od donjeg desnog ka gornjem levom uglu sa punim linijama kao 0 i isprekidanim linijama kao 1 ili od vrha levo do dole desno sa punim linijama kao 1 i isprekidanim linijama kao 0 heksagrami se mogu tumačiti kao niz od 0 do 63.[8]

Indija[uredi | uredi izvor]

Indijski naučnik Pingala (oko 2. veka p. n. e.) razvio je binarni sistem za opisivanje metrike.[9][10] On je koristio binarne brojeve u obliku kratkih i dugih slogova (potonji jednaki dužini sa dva kratka sloga), čineći ga sličnim Morzeovom kodu.[11][12] Oni su bili poznati kao lagu (laki) i guru (teški) slogovi.

Pingalin hinduistički klasik pod nazivom Čandahsastra (8.23) opisuje formiranje matrice kako bi se svakom metru dala jedinstvena vrednost. „Čandahsastra“ se doslovno prevodi kao nauka o metrima na sanskritu. Binarne reprezentacije u Pingalinom sistemu se povećavaju udesno, a ne ulevo kao u binarnim brojevima moderne pozicione notacije.[11][13] U Pingalinom sistemu brojevi počinju od broja jedan, a ne od nule. Četiri kratka sloga „0000” je prvi obrazac i odgovara vrednosti jedan. Brojčana vrednost se dobija tako što se zbiru vrednosti mesta doda jedan.[14]

Druge kulture[uredi | uredi izvor]

Stanovnici ostrva Mangareva u Francuskoj Polineziji koristili su hibridni binarno-decimalni sistem pre 1450. godine.[15] Prorezani bubnjevi sa binarnim tonovima se koriste za kodiranje poruka širom Afrike i Azije.[6] Skupovi binarnih kombinacija sličnih Ji đingu su takođe korišćeni u tradicionalnim afričkim sistemima proricanja kao što je Ifa, kao i u srednjovekovnoj zapadnoj geomanciji.

Zapadni prethodnici Lajbnica[uredi | uredi izvor]

U kasnom 13. veku Ramon Lul je imao ambiciju da objasni svu mudrost u svakoj grani ljudskog znanja tog vremena. U tu svrhu je razvio opšti metod ili 'Ars generalis' zasnovan na binarnim kombinacijama niza jednostavnih osnovnih principa ili kategorija, koji se smatra prethodnikom računarske nauke i veštačke inteligencije.[16]

Godine 1605, Fransis Bejkon je raspravljao o sistemu u kome se slova abecede mogu svesti na sekvence binarnih cifara, koje bi potom mogle biti kodirane kao jedva vidljive varijacije u fontu u bilo kom nasumičnom tekstu.[17] On je napomenuo da je važno za opštu teoriju binarnog kodiranja, da se ovaj metod može koristiti sa bilo kojim objektom: „pod uslovom da ti objekti mogu da imaju samo dvostruku razliku; kao kod zvona, preko truba, pomoću svetla i baklji, prema izveštaju musketa, i bilo kakvih instrumenata slične prirode“.[17] (Pogledajte Bejkonovu šifru.)

Džon Neper je 1617. opisao sistem koji je nazvao lokacijskom aritmetikom za obavljanje binarnih proračuna koristeći nepozicionu reprezentaciju slovima. Tomas Heriot je istraživao nekoliko sistema pozicionog numerisanja, uključujući binarni, ali nije objavio svoje rezultate; pronađeni su kasnije među njegovim papirima.[18] Verovatno je prva publikacija sistema u Evropi bila rad Huana Karamuela i Lobkovica, 1700. godine.[19]

Operacije[uredi | uredi izvor]

  • sabiranje:

 11001+

 01111=

101000

(25+15)=40

  • oduzimanje:

101000-

 01111=

 11001

(40-15)=25

Primena[uredi | uredi izvor]

Binarni brojčani sistem je svoju glavnu primenu našao u računarstvu. Velika većina modernih računara koristi binarnu logiku - to jest podatke zapisuje i interpretira u obliku nula i jedinica.

Zapisivanje brojeva u binarnom sistemu[uredi | uredi izvor]

Da bi se broj preveo iz dekadnog sistema u binarni, potrebno je izvršiti jednostavan postupak deljenjem brojem 2. Ako želimo da napišemo broj 13 u binarnom sistemu, treba da izvedemo sledeći postupak: Najpre ćemo podeliti broj 13 brojem 2:

13:2=6 ostatak 1

Ostatak ćemo zapisati sa strane(1), a količnik(6) nastaviti da delimo:

6:2=3 ostatak 0

Ostatak ćemo zapisati sa strane(0), a količnik(3) nastaviti da delimo:

3:2=1 ostatak 1

Ostatak ćemo zapisati sa strane(1), a količnik(1) nastaviti da delimo:

1:2=0 ostatak 1

Zatim ćemo zapisati sve ostatke suprotnim redom od onog kojim smo ih dobijali(odozdo ka gore):

1101

I dobili smo broj 13 u binarnom sistemu, tj zapisanog samo sa dve cifre.

Svaki broj se pretvara iz dekadnog u binarni sistem brojeva na isti način, tj. deljenjem i pisanjem ostataka od krajnjeg ka početnom, s tim što krajnji količnik mora biti nula, a samim tim i krajnji ostatak 1.

Brojevi se mogu zapisati i u drugim pozicionim sistemima brojeva takođe deljenjem onim brojem koji odgovara broju cifara u tom sistemu (binarni ima 2 cifre pa se brojevi dele brojem 2) i zapisivanjem ostataka.

Vidi još[uredi | uredi izvor]

Reference[uredi | uredi izvor]

  1. ^ Robson, Eleanor; Stedall, Jacqueline, ur. (2009), „Myth No. 2: the Horus eye fractions”, The Oxford Handbook of the History of Mathematics, Oxford University Press, str. 790, ISBN 9780199213122 
  2. ^ Chrisomalis, Stephen (2010), Numerical Notation: A Comparative History, Cambridge University Press, str. 42—43, ISBN 9780521878180 .
  3. ^ Rudman, Peter Strom (2007), How Mathematics Happened: The First 50,000 Years, Prometheus Books, str. 135—136, ISBN 9781615921768 .
  4. ^ a b Edward Hacker; Steve Moore; Lorraine Patsco (2002). I Ching: An Annotated Bibliography. Routledge. str. 13. ISBN 978-0-415-93969-0. 
  5. ^ a b Redmond & Hon (2014), str. 227.
  6. ^ a b Jonathan Shectman (2003). Groundbreaking Scientific Experiments, Inventions, and Discoveries of the 18th Century. Greenwood Publishing. str. 29. ISBN 978-0-313-32015-6. 
  7. ^ Shao Yong's square
  8. ^ Zhonglian, Shi; Wenzhao, Li; Poser, Hans (2000). Leibniz' Binary System and Shao Yong's "Xiantian Tu in :Das Neueste über China: G.W. Leibnizens Novissima Sinica von 1697 : Internationales Symposium, Berlin 4. bis 7. Oktober 1997. Stuttgart: Franz Steiner Verlag. str. 165—170. ISBN 3515074481. 
  9. ^ Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming: the microchip PIC. Boca Raton, Florida: CRC Press. str. 37. ISBN 978-0-8493-7189-9. 
  10. ^ W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, (1995) ISBN 0-387-94544-X
  11. ^ a b Binary Numbers in Ancient India
  12. ^ Math for Poets and Drummers Arhivirano 16 jun 2012 na sajtu Wayback Machine (pdf, 145KB)
  13. ^ Stakhov, Alexey; Olsen, Scott Anthony (2009). The mathematics of harmony: from Euclid to contemporary mathematics and computer science. ISBN 978-981-277-582-5. 
  14. ^ B. van Nooten, "Binary Numbers in Indian Antiquity", Journal of Indian Studies, Volume 21, 1993, pp. 31-50
  15. ^ Bender, Andrea; Beller, Sieghard (16. 12. 2013). „Mangarevan invention of binary steps for easier calculation”. Proceedings of the National Academy of Sciences. 111 (4): 1322—1327. PMC 3910603 Slobodan pristup. PMID 24344278. doi:10.1073/pnas.1309160110 Slobodan pristup. 
  16. ^ (see Bonner 2007 [1] Arhivirano 3 april 2014 na sajtu Wayback Machine, Fidora et al. 2011 [2] Arhivirano na sajtu Wayback Machine (8. april 2019))
  17. ^ a b Bacon, Francis (1605). „The Advancement of Learning”. London. str. Chapter 1. 
  18. ^ Shirley, John W. (1951). „Binary numeration before Leibniz”. American Journal of Physics. 19 (8): 452—454. Bibcode:1951AmJPh..19..452S. doi:10.1119/1.1933042. 
  19. ^ Ineichen, R. (2008). „Leibniz, Caramuel, Harriot und das Dualsystem” (PDF). Mitteilungen der deutschen Mathematiker-Vereinigung (na jeziku: nemački). 16 (1): 12—15. S2CID 179000299. doi:10.1515/dmvm-2008-0009. 

Literatura[uredi | uredi izvor]

  • Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming: the microchip PIC. Boca Raton, FL: CRC Press. str. 37. ISBN 978-0-8493-7189-9. 
  • Redmond, Geoffrey; Hon, Tze-Ki (2014). Teaching the I Ching. Oxford University Press. ISBN 978-0-19-976681-9. 
  • Boyer, Carl B. 1968. History of Mathematics. John Wiley. Reprint Princeton U. Press (1985).
  • Chace, Arnold Buffum. 1927–1929. The Rhind Mathematical Papyrus: Free Translation and Commentary with Selected Photographs, Translations, Transliterations and Literal Translations. 2 vols. Classics in Mathematics Education 8. Oberlin: Mathematical Association of America. (Reprinted Reston: National Council of Teachers of Mathematics, 1979). ISBN 0-87353-133-7
  • Clagett, Marshall. 1999. Ancient Egyptian Science: A Source Book. Volume 3: Ancient Egyptian Mathematics. Memoirs of the American Philosophical Society 232. Philadelphia: American Philosophical Society. ISBN 0-87169-232-5
  • Couchoud, Sylvia. 1993. Mathématiques égyptiennes: Recherches sur les connaissances mathématiques de l'Égypte pharaonique. Paris: Éditions Le Léopard d'Or
  • Daressy, G. "Ostraca," Cairo Museo des Antiquities Egyptiennes Catalogue General Ostraca hieraques, vol 1901, number 25001-25385.
  • Gillings, Richard J. 1972. Mathematics in the Time of the Pharaohs. MIT Press. (Dover reprints available).
  • Imhausen, Annette. 2003. "Ägyptische Algorithmen". Wiesbaden: Harrassowitz
  • Johnson, G., Sriraman, B., Saltztstein. 2012. "Where are the plans? A socio-critical and architectural survey of early Egyptian mathematics"| In Bharath Sriraman, Editor. Crossroads in the History of Mathematics and Mathematics Education. The Montana Mathematics Enthusiast Monographs in Mathematics Education 12, Information Age Publishing, Inc., Charlotte, NC
  • Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 izd.). Dover Publications. ISBN 978-0-486-22332-2. PMID 14884919. 
  • Peet, Thomas Eric. 1923. The Rhind Mathematical Papyrus, British Museum 10057 and 10058. London: The University Press of Liverpool limited and Hodder & Stoughton limited
  • Reimer, David (2014). Count Like an Egyptian: A Hands-on Introduction to Ancient Mathematics. Princeton, NJ: Princeton University Press. ISBN 978-0-691-16012-2. 
  • Robins, R. Gay. 1995. "Mathematics, Astronomy, and Calendars in Pharaonic Egypt". In Civilizations of the Ancient Near East, edited by Jack M. Sasson, John R. Baines, Gary Beckman, and Karen S. Rubinson. Vol. 3 of 4 vols. New York: Charles Schribner's Sons. (Reprinted Peabody: Hendrickson Publishers, 2000). 1799–1813
  • Robins, R. Gay, and Charles C. D. Shute. 1987. The Rhind Mathematical Papyrus: An Ancient Egyptian Text. London: British Museum Publications Limited. ISBN 0-7141-0944-4
  • Sarton, George. 1927. Introduction to the History of Science, Vol 1. Willians & Williams.
  • Strudwick, Nigel G., and Ronald J. Leprohon. 2005. Texts from the Pyramid Age. Brill Academic Publishers. ISBN 90-04-13048-9.
  • Struve, Vasilij Vasil'evič, and Boris Aleksandrovič Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
  • Van der Waerden, B.L. 1961. Science Awakening". Oxford University Press.
  • Vymazalova, Hana. 2002. Wooden Tablets from Cairo...., Archiv Orientalni, Vol 1, pages 27–42.
  • Wirsching, Armin. 2009. Die Pyramiden von Giza – Mathematik in Stein gebaut. (2 ed) Books on Demand. ISBN 978-3-8370-2355-8.

Spoljašnje veze[uredi | uredi izvor]

Binarni sistem na Vikimedijinoj ostavi.
Preuzeto iz „https://sr.wikipedia.org/w/index.php?title=Бинарни_систем&oldid=27549290”