Dopuna do potpunog kvadrata

Dopuna do potpunog kvadrata je tehnika elementarne algebre sa primenama u različitim oblastima matematike. Koristi se, na primer, u algebri pri rešavanju kvadratne jednačine, u analitičkoj geometriji da odredi grafik kvadratne funkcije, u infinitezimalnom računu pri određivanju vrednosti nekih integrala, i pri računanju Laplasovih transformacija. Cilj ove tehnike je da se eliminiše linearni član kvadratnog trinoma.

Drugim rečima, kvadratni trinom oblika

$ax^{2}+bx+c\,\!$

sa transformiše u oblik

$a(\cdots \cdots )^{2}+{\mbox{const}}.\,$

U ovom kontekstu, slobodan član, označen sa const ne zavisi od promenljive x. Izraz u zagradi je oblika (x − const). Dakle, polazni trinom ax² + bx + c  se transformiše u

$a(x-\alpha \,)^{2}+\beta \,$

gde treba odrediti $\alpha \,$ i $\beta \,$.

U matematici je dopuna do potpunog kvadrata osnovna algebarska operacija koja se često bez posebnog naglašavanja primenjuje u različitim računicama sa kvadratnim polinomima.

Pregled

Osnova

Osnova za ovu tehniku je jednostavna formula elementarne algebre za određivanje kvadrata binoma:

$(x+p)^{2}\,=\,x^{2}+2px+p^{2}.\,\!$

Na primer:

${\begin{alignedat}{2}(x+3)^{2}\,&=\,x^{2}+6x+9&&(p=3)\\[3pt](x-5)^{2}\,&=\,x^{2}-10x+25\qquad &&(p=-5).\end{alignedat}}$

Kod bilo kog potpunog kvadrata, broj p je uvek polovina koeficijenta uz x, a slobodan član je jednak p².

Osnovni primer

Neka je dat sledeći kvadratni polinom:

$x^{2}+10x+28.\,\!$

Ovaj trinom nije potpuni kvadrat, pošto 28 nije kvadrat broja 5:

$(x+5)^{2}\,=\,x^{2}+10x+25.\,\!$

Ipak, moguće je polazni polinom zapisati kao zbir kvadrata i konstante:

$x^{2}+10x+28\,=\,(x+5)^{2}+3.$

---

Opšti postupak

Proizvoljan monični kvadratni trinom

$x^{2}+bx+c,\,\!$

je moguće zapisati u obliku kvadrata binoma čija se dva prva člana poklapaju sa datim:

$\left(x+{\tfrac {1}{2}}b\right)^{2}\,=\,x^{2}+bx+{\tfrac {1}{4}}b^{2}.$

Kvadrat ovog binoma se razlikuje od polaznog trinoma samo u vrednosti slobodnog člana. Zato se može zapisati

$x^{2}+bx+c\,=\,\left(x+{\tfrac {1}{2}}b\right)^{2}+\beta \,,$

gde je $\beta \,$ konstanta. Upravo ovaj postupak se naziva dopunom do potpunog kvadrata. Primeri:

${\begin{alignedat}{1}x^{2}+6x+11\,&=\,(x+3)^{2}+2\\[3pt]x^{2}+14x+30\,&=\,(x+7)^{2}-19\\[3pt]x^{2}-2x+7\,&=\,(x-1)^{2}+6.\end{alignedat}}$

Nemonični trinom

Ukoliko je koeficijent uz kvadratni član različit od nule

$ax^{2}+bx+c\,\!$

potrebno je najpre faktorisati polinom u obliku proizvoda koeficijenta a i kvadratnog trinoma, i zatim dopuniti dobijeni monični trinom do potpunog kvadrata.

Primer:

${\begin{aligned}3x^{2}+12x+27&=3(x^{2}+4x+9)\\&{}=3\left((x+2)^{2}+5\right)\\&{}=3(x+2)^{2}+15\end{aligned}}$

Zahvaljujući ovome, moguće je proizvoljan kvadratni polinom zapisati u obliku

$a(x-\alpha \,)^{2}+\beta .\,\!$

Formula

Rezuktat primene tehnike se može zapisati u obliku formule. U opštem slučaju:

$ax^{2}+bx+c\;=\;a(x-\alpha )^{2}+\beta ,\quad {\text{gde je}}\quad \alpha =-{\frac {b}{2a}}\quad \wedge \quad \beta =c-{\frac {b^{2}}{4a}}.$

Posebno, kada je a=1:

$x^{2}+bx+c\;=\;(x-\alpha )^{2}+\beta ,\quad {\text{gde je}}\quad \alpha =-{\frac {b}{2}}\quad \wedge \quad \beta =c-{\frac {b^{2}}{4}}.$

Matrična jednakost je vrlo slična:

$x^{\mathrm {T} }Ax+x^{\mathrm {T} }b+c=(x-\alpha )^{\mathrm {T} }A(x-\alpha )+\beta \quad {\text{gde je}}\quad \alpha =-{\frac {1}{2}}A^{-1}b\quad \wedge \quad \beta =c-{\frac {1}{4}}b^{\mathrm {T} }A^{-1}b$

Veza sa grafikom

Grafici kvadratnih funkcija pomereni duž x-ose za $\alpha \,$ = 0, 5, 10, i 15.

Grafici kvadratnih funkcija pomereni duž y-ose za $\beta \,$ = 0, 5, 10, i 15.

Grafici kvadratnih funkcija pomereni duž x-ose i y-ose za $\alpha \,$ = $\beta \,$ = 0, 5, 10, i 15.

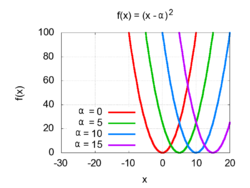
U analitičkoj geometriji, grafik proizvoljne kvadratne funkcije je parabola u xОy-ravni. Ukoliko je kvadratni trinom oblika

$(x-\alpha \,)^{2}+\beta \,\quad \vee \quad a(x-\alpha \,)^{2}+\beta \,$

brojevi $\alpha \,$ i $\beta \,$ se mogu shvatiti kao dekartove koordinate temena parabole. To znači da je $\alpha \,$ x-koordinata ose simetrije, a $\beta \,$ je minimalna (ili maksimalna, ako je a < 0) vrednost kvadratne funkcije.

Drugim rečima, grafik funkcije ƒ(x) = x² je parabola čije je teme u koordinatnom početku (0, 0). Grafik funkcije ƒ(x − $\alpha \,$) = (x − $\alpha \,$)² je parabola pomerena udesno za $\alpha \,$ čije je teme u tački ($\alpha \,$, 0), kao što je prikazano na gornjoj slici. Osim toga, grafik funkcije ƒ(x) + $\beta \,$ = x² + $\beta \,$ je parabola pomerena duž y-ose na pozitivnu stranu za $\beta \,$, te joj je teme u tački (0, $\beta \,$), kao što je prikazano na drugoj slici. Kobinovanjem horizontalnog i vertikalnog pomeranja dobija se ƒ(x − $\alpha \,$) + $\beta \,$ = (x − $\alpha \,$)² + $\beta \,$ što je parabola pomerena udesno za $\alpha \,$ i gore za $\beta \,$ sa temenom u tački ($\alpha \,$, $\beta \,$), kao što se može videti na trećoj slici.

Rešavanje kvadratnih jednačina

Dopuna do potpunog kvadrata se može koristiti za rešavanje proizvoljne kvadratne jednačine. Na primer:

$x^{2}+6x+5=0.\,\!$

U prvom koraku se polazni trinom dopuni do potpunog kvadrata:

$(x+3)^{2}-4=0.\,\!$

Zatim se primeni formula za razliku kvadrata:

$(x+3-2)(x+3+2)=0\,\!$

$(x+1)(x+5)=0\,\!$

Odatle je

$x+1=0\quad \vee \quad x+5=0,$

pa su rešenja polazne jednačine

$x=-1\quad \vee \quad x=-5.$

Ovo se može primeniti na proizvoljnu kvadratnu jednačinu. Kada je koeficijent uz x² različit od 1, prvi korak će biti deljenje jednačine sa tim koeficijentom: pogledati, na primer, ne-monični slučaj.

Iracionalni i kompleksni koreni

Za razliku od metoda koji koriste faktorizaciju jednačine, pouzdanu samo u slučaju kada su koreni racionalni, dopuna do potpunog kvadrata će utvrditi korene kvadratne jednačine čak i tada kada su oni iracionalni ili kompleksni. Na primer, data je jednačina:

$x^{2}-10x+18=0.\,\!$

Nakon dopune do potpunog kvadrata biće

$(x-5)^{2}-7=0,\,\!$

pa je

$(x-5-{\sqrt {7}})(x-5+{\sqrt {7}})=0.\,\!$

Znači da su koreni

$x=5-{\sqrt {7}}\quad \vee \quad x=5+{\sqrt {7}},\,$

što se može zapisati i sa

$x=5\pm {\sqrt {7}}.\,$

Jednačine čiji su koreni kompleksni mogu se rešavati na isti način:

${\begin{array}{c}x^{2}+4x+5\,=\,0\\[6pt](x+2)^{2}+1\,=\,0\\[6pt](x+2+i)(x+2-i)\,=\,0\\[6pt]x\,=\,-2\pm i.\end{array}}$

Nemonična jednačina

Ukoliko je potrebno rešiti kvadratnu jednačinu čiji vodeći koeficijent nije jednak jedinici, najpre je treba podeliti sa tim koeficijentom:

${\begin{array}{c}2x^{2}+7x+6\,=\,0\\[6pt]x^{2}+{\tfrac {7}{2}}x+3\,=\,0\\[6pt]\left(x+{\tfrac {7}{4}}\right)^{2}-{\tfrac {1}{16}}\,=\,0\\[6pt]\left(x+{\tfrac {7}{4}}-{\tfrac {1}{4}}\right)\left(x+{\tfrac {7}{4}}+{\tfrac {1}{4}}\right)\,=\,0\\[6pt]x=-{\tfrac {3}{2}}\quad \vee \quad x=-2.\end{array}}$

Druge primene

Integracija

Ova tehnika se može koristiti za izračunavanje bilo kog integrala oblika

$\int {\frac {dx}{ax^{2}+bx+c}},$

uz upotrebu osnovnih jednakosti:

$\int {\frac {dx}{x^{2}-a^{2}}}={\frac {1}{2a}}\ln \left|{\frac {x-a}{x+a}}\right|+C\quad {\text{and}}\quad \int {\frac {dx}{x^{2}+a^{2}}}={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C.$

Na primer, neka je dat integral:

$\int {\frac {dx}{x^{2}+6x+13}}.$

Dopunom do potpunog kvadrata trinoma u imeniocu dobija se:

$\int {\frac {dx}{(x+3)^{2}+4}}\,=\,\int {\frac {dx}{(x+3)^{2}+2^{2}}}.$

Dobijeni integral se može izračunati korišćenjem smene u = x + 3:

$\int {\frac {dx}{(x+3)^{2}+4}}\,=\,{\frac {1}{2}}\arctan \left({\frac {x+3}{2}}\right)+C.$

Kompleksni brojevi

Ukoliko su u izrazu

$|z|^{2}-b^{*}z-bz^{*}+c,\,$

z i b kompleksni brojevi, z^* i b^* su njihovi konjugati, i neka je c realan broj. Upotrebom identiteta |u|² = uu^* moguće je zapisati dati izraz na sledeći način:

$|z-b|^{2}-|b|^{2}+c,\,\!$

odakle se jasno vidi da je u pitanju realan broj. Zapis sledi iz sledećeg niza jednakosti:

${\begin{aligned}|z-b|^{2}&{}=(z-b)(z-b)^{*}\\&{}=(z-b)(z^{*}-b^{*})\\&{}=zz^{*}-zb^{*}-bz^{*}+bb^{*}\\&{}=|z|^{2}-zb^{*}-bz^{*}+|b|^{2}.\end{aligned}}$

U sledećem izrazu

$ax^{2}+by^{2}+c,\,\!$

neka su a, b, c, x, i y realni brojevi, i neka je a > 0 i b > 0, onda se polazni izraz može prikazati kao kvadrat apsolutne vrednosti kompleksnog broja. Ako se definiše

$z={\sqrt {a}}\,x+i{\sqrt {b}}\,y,$

biće

${\begin{aligned}|z|^{2}&{}=zz^{*}\\&{}=({\sqrt {a}}\,x+i{\sqrt {b}}\,y)({\sqrt {a}}\,x-i{\sqrt {b}}\,y)\\&{}=ax^{2}-i{\sqrt {ab}}\,xy+i{\sqrt {ba}}\,yx-i^{2}by^{2}\\&{}=ax^{2}+by^{2},\end{aligned}}$

pa je

$ax^{2}+by^{2}+c=|z|^{2}+c.\,\!$

Geometrijsko objašnjenje

Neka je potrebno primeniti ovu tehniku na sledeću jednačinu

$x^{2}+bx=a.\,$

Kako x² predstavlja površinu kvadrata stranice x, a bx predstavlja površinu pravougaonika sa stranicama b i x, proces dopune do potpunog kvadrata se može predstaviti vizuelno pomoću odgovarajućih četvorouglova.

Ukoliko se kvadrat x² i pravougaonik bx jednostavno nameste tako da formiraju veći kvadrat, ispostaviće se da njemu fali jedan deo. Član (b/2)² koji se dodaje na obe strane gornje jednačine predstavlja upravo površinu nedostajućeg ćoška, odakle i potiče fraza „dopuna do potpunog kvadrata“.

Varijacija tehnike

Kao što se obično navodi, dopuna do potpunog kvadrata podrazumeva dodavanje trećeg člana, v ² na prva dva člana razvijene formule za kvadrat binoma:

$u^{2}+2uv\,$

čime se dobija pravi kvadrat. U nekim situacijama potrebno je dodati srednji član, ili kao 2uv ili −2uv, na izraz oblika:

$u^{2}+v^{2}\,$

čime se ponovo dobija potpuni kvadrat.

Primer: zbir pozitivnog broja i njegove recipročne vrednosti

Kako važi

${\begin{aligned}x+{1 \over x}&{}=\left(x-2+{1 \over x}\right)+2\\&{}=\left({\sqrt {x}}-{1 \over {\sqrt {x}}}\right)^{2}+2\end{aligned}}$

sledi da je zbir pozitivnog broja x i njegove recipročne vrednosti uvek veći ili jednak 2. Kako je kvadrat realnog izraza uvek veći ili jednak nuli, dobija se navedeno ograničenje; jendakost sa 2 se postiže samo onda kada je x = 1, čime se eliminiše kvadratni sabirak.

Primer: faktorizacija jednostavnog polinoma četvrtog stepena

Neka je dat binom

$x^{4}+324.\,\!$

On se može napisati u obliku

$(x^{2})^{2}+(18)^{2},\,\!$

gde je srednji član 2(x²)(18) = 36x². Odatle sledi

${\begin{aligned}x^{4}+324&{}=(x^{4}+36x^{2}+324)-36x^{2}\\&{}=(x^{2}+18)^{2}-(6x)^{2}\\&{}=(x^{2}+18+6x)(x^{2}+18-6x)\\&{}=(x^{2}+6x+18)(x^{2}-6x+18)\end{aligned}}$

(u poslednjem redu su monomi poređani po opadajućim stepenima).

Spoljašnje veze

• Completing the square na mathworld.wolfram.com (jezik: engleski)
• Completing the square na planetmath.org (jezik: engleski)