Loranov red

Loranov red se definiše u odnosu na određenu tačku c i putanju integracije γ. Putanja integracije mora ležati u prstenu (prikazanom crvenom bojom) u kojem je funkcija f(z) holomorfna (integracija)

U matematici, Loranov red kompleksne funkcije f(z) predstavlja istu tu funkciju predstavljenu kao stepeni red koji obuhvata i članove sa negativnim indeksom. Može se koristiti da bi se se izrazila kompleksna funkcija tamo gdje se ne može primijeniti Tejlorov red. Loranov red je dobio ime po Pjeru Alfonsu Loranu, koji ga je prvi objavio 1843. godine. Karl Vajerštras ga je možda otkrio ranije, još 1841. godine, ali ga u svakom slučaju nije tada objavio.

Loranov red kompleksne funkcije f(z) u okolini tačke c ima sljedeći oblik:

$f(z)=\sum _{n=-\infty }^{\infty }a_{n}(z-c)^{n}$

pri čemu su a_n konstante koje se dobijaju rješavanjem krivolinijskog integrala koji predstavlja uopštenje Košijeve integralne formule:

$a_{n}={\frac {1}{2\pi i}}\oint _{\gamma }{\frac {f(z)\,dz}{(z-c)^{n+1}}}.\,$

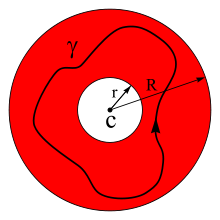
Kriva po kojoj integralimo, kriva γ, pozitivno je orijentisana (kreće se u smjeru suprotnom od kazaljke na satu), zatvorena, dio-po-dio glatka i nema presjeka sa samom sobom, a leži u prstenu A u kom je funkcija analitička (holomorfna). Razvoj f(z) će na taj način biti valjan svuda na prstenu. U slici desno, prsten je prikazan crvenom bojom, a primjer krive koja se može koristiti kao staza integracije označen je sa γ. Ako za γ uzmemo kružnicu $|z-c|=\varrho$, sa $r<\varrho <R$, problem se svodi na izračunavanje kompleksnih Furijeovih koeficijenata restrikcije $f$ na $\gamma$. Činjenica da ovi integrali ne zavise od oblika krive $\gamma$ predstavlja direktnu posljedicu Stouksove teoreme.

Konvergentni Loranovi redovi

Funkcija e^−1/x2 i Loranove aproksimacije iste: različite boje oslikavaju različite stepene razvoja.

Loranovi redovi sa kompleksnim koeficijentima predstavljaju važan alat u kompleksnoj analizi, naročito u cilju izučavanja ponašanja funkcije u blizini singulariteta.

Neka je data funkcija ƒ(x) = e^−1/x2, ƒ(0) = 0. Gledana kao realna funkcija, ona je beskonačno diferencijabilna u svim tačkama realne ose; međutim, gledana kao kompleksna funkcija, ona nije diferencijabilna u tački 0. Ako uvedemo smjenu x umjesto −1/x², dobijamo Loranov red koji konvergira i jednak je funkciji ƒ(x) za sve kompleksne brojeve x osim singulariteta u tački 0. Na slici desno može se vidjeti -{ƒ(x) = e^−1/x2 crnom bojom, a aproksimacije

$\sum _{n=0}^{N}(-1)^{n}\,{x^{-2n} \over n!}$

za N = 1, 2, 3, 4, 5, 6, 7 i 50. Kako N teži beskonačno, aproksimacija će težiti upravo toj funkciji i biće joj potpuno jednaka u svim tačkama osim u singularitetu 0.