Metoda polovljenja intervala

Nekoliko koraka metode polovljenja intervala, primenjenog nad početnim intervalom [a₁;b₁]. Veća crvena tačka je nula funkcije.

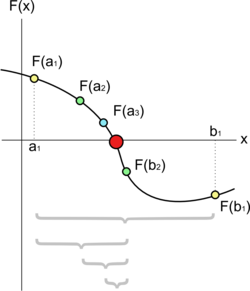
U numeričkoj analizi, metoda polovljenja intervala je algoritam za približno rešavanje jednačina, koji funkcioniše tako što ponavlja postupak deljenja intervala na pola i izbora podintervala u kome se nalazi nula funkcije.

Pretpostavimo da želimo da rešimo jednačinu f(x) = 0. Date su dve tačke a i b, takve da su f(a) i f(b) suprotnog znaka. Ukoliko je funkcija neprekidna, znamo da ona mora da ima najmanje jednu nulu u intervalu [a, b]. Metoda polovljenja intervala deli interval na dva dela računajući c = (a+b) / 2. Postoje dve mogućnosti: ili f(a) i f(c) imaju suprotne znakove, ili f(c) i f(b) imaju suprotne znakove (pretpostavimo da u intervalu postoji samo jedna nula, i ona se ne nalazi u tački c). Algoritam polovljenja intervala se zatim ponovo primenjuje na podinterval u kome se promena znaka odigrala. Ovaj algoritam je po svojoj prirodi rekurzivan.

Metoda polovljenja intervala je manje efikasna od metode tangente (Njutnove metode), ali je manje sklona čudnom ponašanju.

Ako je f neprekidna funkcija na intervalu [a, b] i f(a)f(b) < 0, tada metoda polovljenja intervala konvergira nuli funkcije f. U stvari, apsolutna greška za metodu polovljenja intervala je najviše

${\frac {\left|b-a\right|}{2^{n}}}$

nakon n koraka. Drugim rečima, greška se polovi u svakoj iteraciji, pa metod konvergira linearno, što je prilično sporo. Sa pozitivne strane, metod garantovano konvergira ako su f(a) i f(b) suprotnih znakova.

Pseudokod

Sledi reprezentacija metode polovljenja intervala u Visual Basic kodu. Promenljive xL i xR odgovaraju a i b. Početne vrednosti xL i xR moraju biti izabrane tako da su f(xL) i f(xR) suprotnog znaka (da zagrađuju koren). Promenljiva epsilon određuje koliko će rezultat biti precizan.

 'Bisection Method
 
 'Start loop
 Do While (xR - xL) > epsilon
   
   'Calculate midpoint of domain
   xM = (xR + xL) / 2
   
   'Find f(xM)
   If ((f(xL) * f(xM)) > 0) Then
     'Throw away left half
     xL = xM
   Else
     'Throw away right half
     xR = xM
   End If
 Loop

Vidi još

• Binarna pretraga

Spoljašnje veze

• Metoda polovljenja intervala na Mathcad Application Server
• Metoda polovljenja intervala
• True example of using bisection method in computer programming free program to isoelectric point calculation

Literatura

• Richard L. Burden, J. Douglas Faires (2000), "Numerical Analysis, (7th Ed)", Brooks/Cole. ISBN 978-0-534-38216-2.