Mehanički rad

Rad
Bacač u bejzbolu pozitivno deluje na loptu primenjujući na nju silu na rastojanju na kome se kreće.
Uobičajeni simboli	W
SI jedinica	džul (J)
Druge jedinice	stopa-funta, [[Erg]]
U SI baznim jedinicama	1 kg⋅m2⋅s−2
SI dimenzija	M L2 T−2
Derivacije iz drugih kvantiteta	W = F ⋅ s W = τ θ

Rad u fizici je prenos energije iz jednog sistema u drugi. Ovaj prenos se u klasičnoj mehanici vrši delovanjem sile duž nekog puta. Rad je u stvari jednak proizvodu sile i pređenog puta, ako sila deluje u pravcu pomeranja tela. U polju konzervativne sile rad ne zavisi od oblika puta, već samo od početne i krajnje tačke.

Rad je skalarna veličina. Jedinica za rad u Međunarodnom sistemu jedinica je džul (J), koji predstavlja:

$\mathrm {J={\frac {kg\,m^{2}}{s^{2}}}}$

Fizičku veličinu proizvoda sile i dužine je u fiziku uveo naučnik Gaspar Gistav Koriolis 1830-ih.

Matematička definicija

Jednostavniji oblik definicije rada je sveden na pretpostavku konstantne vrednosti sile i pravolinijske putanje. Tada se mehanički rad može definisati kao skalarni proizvod vektora sile i vektora pomeraja.

$A={\vec {F}}\cdot {\vec {r}}$

Prethodno pomenuta definicija rada ima svoja ograničenja. Ona važi pod uslovom da je sila konstantna, a putanja tela nije krivudava. Stoga je potrebno uvesti matematički pravilniju definiciju, koja se zasniva na ideji da se krivudava putnja podeli na veliki broj manjih, približno pravih delova delova. Otuda se dobija obrazac:

$A\approx \sum _{i=1}^{N}A_{i}=\sum _{i=1}^{N}{\vec {F}}(\mathbf {s} _{i})\Delta {\vec {s}}_{i}\,.$

Odakle:

$A=\int _{\mathbf {s} _{1}}^{\mathbf {s} _{2}}{\vec {F}}(\mathbf {s} )\,\mathrm {d} {\vec {s}}\,,$

Iz gornje jednačine sledi da je rad ($A\,$) jednak integralu skalarnog proizvoda vektora sile (${\vec {F}}$) i infinitezimale vektora puta (${\vec {s}}$).

Odnos snage i rada

Rad se može računati i kao proizvod snage i vremena :

$A=P\cdot t$

Ovo važi u situaciji kada je snaga nepromenljiva tokom vremena.

Primer

U ovom primeru sila i smer (putanja tela) su kolinearni. Pretpostavimo da se kamen mase 10 kg nalazi na tlu, i da treba da ga podignemo vertikalno uvis do visine h = 1,5 m. Ubrzanje sile teže g = 9,81 m/s².

m = 10 kg

h = 1,5 m

g = 9,81 m/s²

Sila gravitacije F koja deluje na kamen je:

$F=m\cdot g=10\cdot 9,81=98,1N$

Odatle, uloženi rad pri podizanju kamena se dobija kao:

$A=F\cdot h=98,1\cdot 1,5=147,15J$

Specijalni slučaj „sila puta put”

Najjednostavnija formula za rad sile, koja je najbolje polazište za razumevanje pojma rada, vredi npr. u slučaju kada konstantna sila deluje na telo koje se translacijski (tj. bez rotacije) kreće u smeru njenog delovanja. Tada je (kao što proizlazi i iz gornjeg integrala):

$W=Fs\,$

gde je F iznos sile, dok je s pređeni put. Na taj se slučaj odnosi definicija iz osnovne škole „rad je sila puta put”, koja ne uzima u obzir da je sila vektor (što je ovde irelevantno zato što su i sila i kretanje u istom smeru koji se ne menja), niti precizira da treba promatrati put hvatišta sile (jer se sve tačke tela jednako kreću, te može biti i „put tela”). Npr. ako sila od 5 N vuče telo na putu od 3 m, ona izvrši rad W = Fs = 5 N ∙ 3 m = 15 J. Odatle se vidi da je SI merna jedinica za rad, džul (J), skraćenica za umnožak „Nm”.

Ipak, ova jednostavna formula nije ograničena samo na pravolinijsko kretanje. Ona vredi uvek kada se iznos sile ne menja, a hvatište sile se kreće tačno u smeru delovanja sile (koji se može po volji menjati).

Zakon o promeni kinetičke energije

Odnos rada i promene energije ključna je odrednica za razumevanje definicije rada sile. Ako je u prethodnom jednostavnom primeru sila F jedina sila koja deluje na telo mase m koje je do tada mirovalo (nije imalo kinetičke energije), telo na putu s ima stalno ubrzanje a = F/m i kreće se jednoliko ubrzano, te na kraju puta s = at²/2 postiže brzinu v = at. Odatle se lako vidi da je rad sile jednak kinetičkoj energiji koju telo dobije na tom putu:

$W=Fs=ma{\frac {at^{2}}{2}}=m{\frac {(at)^{2}}{2}}={\frac {mv^{2}}{2}}=E_{k}$

Poopštenje tog rezultata (moglo bi se dobiti iz opšte formule za rad sile, uz malo više računa) zove se zakon o promeni kinetičke energije: rad svih sila koje deluju na kruto telo jednak je promeni njegove kinetičke energije. Pritom treba imati na umu da kinetička energija tela ne mora biti samo translacijska (kako je opisana u gornjem jednostavnom primeru), nego može imati i rotacijski deo (osim u slučaju čestice, tj. tela zanemarivih dimenzija).

Objašnjenje definicije rada sile

Objašnjenje opšte formule za rad sile polazi od opisane veze s energijom: formula je konstruirana upravo tako da promena kinetičke energije bude jednaka ukupnom radu svih sila.

Značaj tangencijalne komponente sile

Dekompozicija sile na tangencijalnu i normalnu vektorsku komponentu

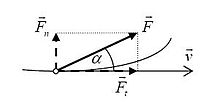
Prva posledica te veze jeste da sila koja deluje na česticu okomito na smer njenog kretanja (kaže se: normalna sila; primer: centripetalna sila) ne vrši rad – jer ne menja iznos brzine (nego samo njen smer) te ne utiče na kinetičku energiju čestice. Sila koja leži na pravcu kretanja čestice (kaže se: tangencijalna sila) vrši pozitivan rad ako je u smeru kretanja, jer povećava brzinu a time i kinetičku energiju čestice, odnosno negativan rad ako je u suprotnom smeru od kretanja, jer umanjuje kinetičku energiju. Zato se proizvoljni vektor sile ^{$\scriptstyle {\vec {F}}$} prikaže kao zbir tangencijalne i normalne sile (formalnije rečeno: rastavi na tangencijalnu i normalnu vektorsku komponentu), od čega se za proračun rada koristi samo tangencijalna. Pritom je F cos α tangencijalna skalarna komponenta vektora sile ^{$\scriptstyle {\vec {F}}$}, tj. to je broj koji je jednak iznosu tangencijalne vektorske komponente sile ako je ona u smeru kretanja, odnosno njenom negativnom iznosu ako je u suprotnom smeru (što daje i odgovarajući predznak rada).

Uloga hvatišta sile

Računanje rada pomoću puta koji prelazi hvatište sile (dok druge tačke tela mogu prelaziti različite puteve) takođe je posledica opisane veze s energijom. Sila pri toj brzini se računa kao translacijska kinetička energija tela. Ako pravac delovanja sile ne prolazi kroz centar mase, osim opisanog učinka sila daje telu i ugaono ubrzanje α, te mu menja i rotacijsku kinetičku energiju. Tada sila mora vršiti veći rad nego kad deluje na centar masa, a to se dešava zato što njeno hvatište prelazi veći put nego što je put centar masa (tj. „put tela”). Zakon poluge još jasnije dokazuje da se rad sile računa pomoću puta hvatišta sile: na većem kraku dovoljna je manja sila za isti rad zato što njeno hvatište prelazi veći put.

Promenjivu silu treba integrisati

Rad sile se može izračunati kao umnožak dva broja (komponente F cos α i puta njenoga hvatišta s) samo ako se zna koliko ti brojevi iznose, tj. ako se na odabranom putu tangencijalna skalarna komponenta sile ne menja. No, u opštem slučaju sila može proizvoljno menjati iznos i smer: tada se rad mora računati pomoću integrala, jer ne postoji jednostavniji postupak da se odredi prosečna vrednost F cos α za računanje rada na nekom putu.

Tumačenje i primer integrala rada

Postupak integrisanja može se najlakše razumeti kao zamisli da se sabiraju radovi promatrane sile po vrlo malim komadima ukupnoga puta, tako malima da se sila na pojedinom komadiću „ne stigne” da se promeni. Naravno, sve dok je broj komadića konačan, sila će se na svakome bar malo promeniti (ako se stalno menja), ali ta promena može biti u tako dalekoj decimali da je to u konačnom rezultatu zanemarljivo (te se uzima bilo koja vrednost s pojedinog komadića puta). Ako to nije slučaj, put se može podijeliti u još sitnije komadiće pre zbrajanja radova, sve dok ne dobije rezultat koji je tačan u željenom broju decimalnih mesta (što se proverava poređenjem s narednom još sitnijom razdeobom puta). Takav se postupak zove numeričko integrisanje.

Proces usitnjavanja se može misaono nastaviti u nedogled, znajući da se tako dobijaju uzastopni rezultati sa sve većim brojem tačnih cifara. Integral je (ako postoji) onaj broj (granična vrednost ili limes) kojim se ti uzastopni zbirovi sve manjih komadića rada sve više približavaju (uz dovoljno usitnjavanje puta, zbroj radova je po volji blizu granične vrednosti). A kako pokazuje matematička analiza, ta tačna granična vrednost se može za mnoge konkretne sile izračunati na potpuno drugačiji način, pomoću pravila integrisanja za pojedine vrste funkcija. Na primer, rad se integriše tako što se eksponent uveća za 1, i potom se podeli s novim eksponentom. Za rastezanje elastične opruge (učvršćene na drugom kraju) potrebna je sila F = ks promenjljivog iznosa i u smeru rastezanja, gde je k konstanta opruge, dok je s produženje (potencijal s na prvu), tj. put što ga je prešlo hvatište sile od nerastegnutog položaja s = 0. Da bi rastegnula oprugu za iznos A, sila će izvršiti rad:

$W=\int _{0}^{A}ks\,\mathrm {d} s=k\int _{0}^{A}s\,\mathrm {d} s=k\left[{\frac {s^{2}}{2}}\right]_{0}^{A}={\frac {kA^{2}}{2}}$

Na znaku integrala (stilizovani rastegnuti znak sume, najavljuje sabiranje „beskonačno mnogo beskonačno malih sabiraka”) donja i gornja granica označavaju početnu i završnu tačku puta. Sledi iznos sile ks (kosinusa nema, jer je jednak 1), što se zove podintegralna funkcija. Integral se završava diferencijalom puta ds (koji se može smatrati „beskonačno malim komadićem puta”). (Standardna matematička analiza smatra ovakav „tehničarski” opis nekorektinim, ali noviji radovi pokazuju da se može rigorozno opravdati.) U narednom koraku „vadi” se ispred integrala konstanta koja množi ostatak podintegralne funkcije, a potom se s¹ integriše u s²/2. U zadnjem koraku uvrste se, umesto s, granice integrisanja: najpre gornja granica A, od čega se oduzme isti izraz sa uvršenom donjom granicom (ovde 0, te se ne piše).

Opis rada skalarnim produktom

Skalarnim množenjem dva vektora dobija se skalar koji je jednak umnošku njihovih iznosa i kosinusa ugla među njima. Ako je sila ^{$\scriptstyle {\vec {F}}$} konstantnog iznosa i smera, a smer pravolinijskog kretanja njenog hvatišta zatvara stalni ugao α sa smerom sile, rad se može zapisati na dva načina:

$W=Fs\cos \alpha ={\vec {F}}\cdot {\vec {d}}$

Drugi izraz označava skalarni produkt vektora sile i vektora pomaka ^{$\scriptstyle {\vec {d}}$} (engleski naziv množenja dot product potiče od tačke koja se piše među vektorima). Pomak je usmerena dužina koja „ide” od početne do završne tačke puta na putanji hvatišta sile (opisuje koliko se i u kojem smeru ta tačka „pomakla”). Jednakost navedenih izraza je očigledna iz definicije skalarnog produkta, budući da je u opisanom slučaju iznos pomaka jednak putu s. Može se pokazati da formula sa skalarnim produktom sile i pomaka vredi i za proizvoljni oblik putanje, uz uslov da sila ne menja iznos i smer.

Za proizvoljni oblik putanje hvatišta, potrebno je najpre matematički opisati krivulju duž koje se ta tačka kreće. Kretanje tačke u celosti je opisano ako za svaki trenutak znaju njene koordinate, npr. x(t), y(t) i z(t) u pravougaonom Kartezijevom sistemu gde se možu smatrati skalarnim komponentama vektora položaja (radijus vektora) $\scriptstyle {\vec {r}}(t)$ te tačke. Vektor položaja je usmerena dužina kojoj je početak u išodištu sistema a kraj (strelica) „prati” tačku po putanji. Koordinate i vektor položaja često se pišu bez eksplicitne oznake zavisnosti od vremena, jer se ona kod kretanja tačke i tako podrazumeva.

Kod takvog opisa kretanja, prikladnije je za vektor pomaka iz neke tačke 1 u tačku 2 koristiti oznaku $\scriptstyle \Delta {\vec {r}}$ (ako se zna da $\scriptstyle \Delta$ označava razliku odnosno promenu) jer ona eksplicitno pokazuje da se pomak dobija oduzimanjem pripadnih vektora položaja: $\scriptstyle \Delta {\vec {r}}={\vec {r}}_{2}-{\vec {r}}_{1}$, tj. da se pomak može promatrati kao „promenu položaja”. Dužina putanje (pređeni put s) na krivulji može biti znatno veća od iznosa vektora pomaka $\scriptstyle |\Delta {\vec {r}}|$. Ako se promatraju sve manji pomaci (vremenski interval $\scriptstyle \Delta t$ između promatranih položaja "teži" prema nuli; na skici je ilustrovan početak graničnog procesa) iznosi puta i pomaka postaju sve više jednaki. Jednakost graničnih vrednosti može se zapisati pomoću diferencijala: $\scriptstyle |\mathrm {d} {\vec {r}}|=\mathrm {d} s$. Stoga se integral iz opšte definicije za rad proizvoljne sile na proizvoljnom putu može kraće zapisati pomoću skalarnog produkta:

$W=\int _{A}^{B}{\vec {F}}\cdot \mathrm {d} {\vec {r}}$

Uzimajući u obzir da je brzina $\scriptstyle {\vec {v}}$ neke tačke derivacija njenog vektora položaja po vremenu (te je $\scriptstyle \mathrm {d} {\vec {r}}={\vec {v}}\mathrm {d} t$), može se taj integral prevesti u integral po vremenu:

$W=\int _{A}^{B}{\vec {F}}\cdot {\vec {v}}\,\mathrm {d} t$

Podintegralna funkcija $\scriptstyle {\vec {F}}\cdot {\vec {v}}$ je snaga sile. Budući da se snaga definiše kao derivacija rada po vremenu, jasno je da rad mora biti jednak integralu snage po vremenu.

Literatura

• Jammer, Max (1957). Concepts of Force. Dover Publications, Inc. ISBN 978-0-486-40689-3. 
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th izd.). Brooks/Cole. ISBN 0-534-40842-7. 
• Tipler, Paul (1991). Physics for Scientists and Engineers: Mechanics (3rd ed., extended version izd.). W. H. Freeman. ISBN 0-87901-432-6. 
• Robert Stawell Ball (1871) Experimental Mechanics from Google books.
• Landau, L. D.; Lifshitz, E. M. (1972). Mechanics and Electrodynamics, Vol. 1. Franklin Book Company, Inc. ISBN 978-0-08-016739-8. 

Spoljašnje veze

• Work–energy principle