Minimaks (algoritam)
Minimaks je pravilo odluka koji se koristi u teoriji odlučivanja, teoriji igara, statistici i filozofiji za minimiziranje mogućih gubitaka u najgorim slučajevima(najveći gubitak). Alternativno, može se posmatrati kao maksimiziranje minimalne dobiti. Prvobitno je formulisan za teoriju nulte-sume dva igrača, koji pokriva oba slučaja gde igrači uzimaju alternativne poteze i one gde čine simultane poteze, takođe je proširena na više kompleksnih igara i na opšte odlučivanje u prisustvu neizvesnosti.
Teorija igara[uredi | uredi izvor]
U teoriji simultanih igara, strategija Minimaks je mešovita strategija koja je deo rešenja do nultog zbira igre. U nulta-suma igri, Minimaks rešenje je isto kao i Neš ekvilibrijum.
Minimaks teorema[uredi | uredi izvor]
Stanja minimaks teoreme[1]
Za svake dve osobe, nulta-suma igra sa konačno mnogo strategija, gde postoji vrednost V i mešana strategija za svakog igrača, kao
- (a) S obzirom na strategiju 2 igrača, najbolja isplata za igrača 1 je V, i
- (b) S obzirom na strategiju 1 igrača, najbolja isplata za igrača 2 je -V.
Ekvivalentno, strategija igrača 1 mu garantuje isplatu od V bez obzira na strategiju igrača 2, i slično igrač 2 može sebi garantovati isplatu od -V. Ime Minimaks nastaje jer svaki igrač smanjuje maksimalnu moguću zaradu za druge - jer je igra sa nultom sumom, on takođe smanjuje svoju maksimalnu gubitak (tj. maksimalizuje svoj minimalni gubitak).
Ova teorema je prvo objavljena 1928 godine. od John von Neumann,[2] koji je napisao "As far as I can see, there could be no theory of games … without that theorem … I thought there was nothing worth publishing until the Minimax Theorem was proved".[3]
Pogledati Sion's minimax theorem i Parthasarathy's theorem za generalizaciju; Takođe pogledati example of a game without a value.
Primer[uredi | uredi izvor]
| B bira B1 | B bira B2 | B bira B3 | |
|---|---|---|---|
| A bira A1 | +3 | −2 | +2 |
| A bira A2 | −1 | 0 | +4 |
| A bira A3 | −4 | −3 | +1 |
U ovom primeru je igra nulta-suma, gde A i B prave simultane poteze, ilustujući minimaks rešenja. Pretpostavimo da svaki igrač ima tri moguća poteza i pogledati matricu isplate za A prikazanu sa desne strane. Pretpostavimo da je matrica isplate za B ista matrica sa obrnutim znacima (tj. ako su izbori A1 i V1 onda B plaća 3 A). Onda, minimaksov izbor za A je A2 kako je tada najgori mogući rezultat platiti 1, dok jednostavni minimaksov izbor za B je B2 i najgori mogući rezultat tada je da se ne plati ništa. Naime, ova situacija nije stabilna, jer ako B veruje da će A izabrati A2 onda će B izabrati V1 da bi osvojio 1; onda ako A veruje da će B izabrati B1 onda će A izabrati A1 da osvoji 3; i onda će B izabrati B2; i potencijalno će oba igrača shvatiti težinu samog izbora. Samim tim nam je potrebna stabilnija strategija.
Neki izbori su dominantniji od drugih i mogu biti eliminisani: A neće izabrati A3 kako ni A1 ni A2 neće imati bolje rezultate, bez obzira na izbor koji će napraviti B; B neće izabrati B3 kako će neke mešavine od V1 i V2 napraviti bolje rezultate, bez obzira šta A izabere.
A može da ibegne da napravi očekivanu isplatu veću od 1/3 birajući A1 sa verovatnoćom 1/6 i A2 sa verovatnoćom 5/6: Očekivana isplata za A će biti 3*(1/6)-1*(5/6)=-1/3 u slučaju da B izabere B1 i -2*(1/6)+0*(5/6)=-1/3 u slučaju da B izabere B2. Slično, B može da osigura očekivan dobitak od najmanje 1/3, bez obzira šta A izabere, koristeći slučajnu strategiju odabira V1 sa verovatnoćom 1/3 i B2 sa verovatnoćom 2/3. Ove mešane strategije su sada stabilne i ne mogu se poboljšati.
Maksmin[uredi | uredi izvor]
Često, u teoriji igara, maksmin je drugačije od minimaks. Minimaks se koristi u nulta-suma igrama da označi minimiziranje protivnikove maskimalne zarade. U nultim-sumama, ovo je identično sa minimizovanjem maksimalnog gubitka, i maksimizovanjem minimalnog dobitka.
"Maksmin" je termin koji se obično koristi za nenulta-suma igre pri objašnjavanju gde se maksimizuje minimalni dobitak. U nenulta-suma igrama, ovo nije generalno isto kao minimizovanje protivnikovog maksimalnog dobitka, kao ni Neš ekvilibrijum strategija.
Kombinatornna teorija igara[uredi | uredi izvor]
U kombinatornoj teoriji igara (combinatorial game theory), postoji minimaks algoritam kao rerešenje igara.
A jednostavna verzija minimaks algoritma, navedena u nastavku, baveći se igrama kao što su iks-oks, gde svaki igrač može da pobedi, izgubi, ili izjednači. Ako igrač A može da pobedi u jednom potezu, njegov najbolji potez je taj pobednički potez. Ako igrač V zna da će taj jedan potez odvesti do situacije gde A može da pobedi u jednom potezu, dok će drugi potez odvesti do toga da A može, u najboljem slučaju, da izjednači, onda će najbolji potez igrača V biti da odvede do izjednčenja. Kasnije u igri, lako je videti koji je "najbolji" pokret. Minimaks algoritam pomaže u pronalasku najboljeg poteza, gledanjem unazad od početka. U svakom koraku pretpostavljamo da je igrač A pokušao da maksimizuje šanse pobede A, dok na sledećem krugu ugrač B pokušava da minimizuje šanse da A pobedi(tj. kako bi se igraču V povećala šansa da pobedi).
Minimaks algoritam sa alternativnim pokretima[uredi | uredi izvor]
Minimaks algoritam[4] je rekurzivni algoritam za odabir sledećeg poteza u n-igrača igrama, uglavnom za dva igrača. Vrednost je povezana sa svakom pozicijom ili stanjem igre. Ova vednost se izračunava pomoću funkcije evaluacije pozicije i pokazuje koliko ta pozicija može značiti igračima. Igrač onda pravi potez koji maksimizuje minimalnu vrednost položaja protivnikovih mogućih poteza. Ako se A pokrenuo, A daje vrednost svakom od njegovih legalnih poteza.
Moguća alokacija metoda se sastoji iz dodeljivanja pobede za A kao +1 i za B kao −1. Ovo vodi na kombinatornu teoriju igara razvijenu od strane John Horton Conway. Alternativno korišćenje pravila je ako je rezultat poteza pobeda za A dodeljuje se pozitivna beskonačnost i, ako je rezultat pobeda za B, dodeljuje se negativna beskonačnost. Vrednost A bilo kog sledećeg poteza je minimum vrednosti koje su nastale od svakog od B's mogućih odgovora. Iz ovog razloga, A zovemo maximizing player i B zovemo minimizing player, otuda naziv minimaks algoritam. Algoritam iznad će dodeliti vrednost pozitivne ili negativne beskonačnosti svakoj poziciji dok vrednost svake pozicije ne postane vrednost finalne pozicije pobede ili poraza. Ovo je generalno moguće na kraju komplikovane igre kao što je šah ili go, kako nije računski izvodljivo videti kraj igre, osim pri kraj igre, i umesto pozicija koje daju krajnje vrednosti kao procena stepeni verovanja da oni vode do pobede jednog igrača ili drugog.
Ovo može biti prošireno ako možemo da pružimo heurističnu evaluaciju funkcija koje dodeljuju vrednosti ne završnom potezu bez uzimanja u obzir sve mogućnosti pratećih kompletnih sekvenci. Tako možemo ograničiti minimaks algoritam tako što gledamo samo određeni broj poteza napred. Ovaj broj se zove "look-ahead", meren u "plies (Ply (chess))". Na primer, šah računar IBM Deep Blue (koji pobeđuje Gari Kasparov) gledao je unapred 12 slojeva, zatim primenjuje heuristike evaluacione funkcije.
Algoritam se može posmatrati kao istraživanje čvorova (node (computer science)) kod drveta igara(game tree). Efikasan faktor grananja (branching factor) drveta je srednja vrednost dete čvora svakog čvora (tj. srednja vrednost legalnih poteza na poziciju). Broj čvorova koji se uglavnom istražuju se povećavaju eksponencijalno (exponential growth) sa brojem slojeva(manje je od eksponencijalnog ako se evaluira grub potez ili ponavljanje pozicija). Broj čvorova koji se istražuju za analize igre je dakle približno faktor grananja povećao do jačine broja slojeva. On je dakle nepraktičan (Computational complexity theory#Intractability) da bi se završila analiza igara kao što je šah koristeći minimaks algoritam.
Performanse naivnog minimaks algoritma mogu biti dramatično unapređene, bez odražavanja na rezultat, koristeći alfa-beta pretraga. Ostale heurističke metode mogu takođe da se koriste, ali ne može se za sve njih garatnovati da će dati rezultate kao nepromenjena pretraga.
Naivni minimaks algoritam može trivijalno izmenjen da dodatno vrati celu glavnu varijaciju (Variation (game tree)#Principal variation) zajedno sa maksimalnim rezultatom.
Lua example[uredi | uredi izvor]
function minimax(node,depth)
if depth <= 0 then
-- позитивне вредности су добре за максимизирање играча
-- негативне вредности су добре за минимизирање играча
return objective_value(node)
end
-- максимизирање играча је (+1)
-- минимизирање играча је (-1)
local alpha = -node.player * INFINITY
local child = next_child(node,nil)
while child ~= nil do
local score = minimax(child,depth-1)
alpha = node.player==1 and math.max(alpha,score) or math.min(alpha,score)
child = next_child(node,child)
end
return alpha
end
Pseudokod[uredi | uredi izvor]
Pseudokod za dubinu ograničenu minimaks algoritmom je u nastavku.
function minimax(node, depth, maximizingPlayer)
if depth = 0 or node is a terminal node
return the heuristic value of node
if maximizingPlayer
bestValue := -∞
for each child of node
val := minimax(child, depth - 1, FALSE))
bestValue := max(bestValue, val);
return bestValue
else
bestValue := +∞
for each child of node
val := minimax(child, depth - 1, TRUE))
bestValue := min(bestValue, val);
return bestValue
(* Initial call for maximizing player *)
minimax(origin, depth, TRUE)
Minimaks tretira dva igrača (maksimiziranjem igrača i mininiziranjem istog) podeljeno u dva koda. Na osnovu zapažanja da , minimaks može često da se uprosti u negamaks(negamax) algoritam.
Primer[uredi | uredi izvor]
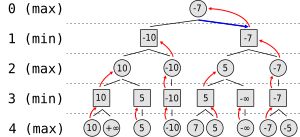

Pretpostavimo da igra počinje, i da maksimum dva poteza po igračuu je po krugu. Algoritam generiše drvo (game tree) nadesno, gde krugovi prestavljaju pokrete igrača koji su pokrenuli algoritam (maximizing player), i kvadratna reprezentacija pokreta protivnika (minimizing player). Iz razloga limitacijenad računarskih resursa, objašnjeno iznad, drvo je limitirano na look-ahead 4 poteza.
Algoritam procenjuje svaki list čvor koristeći funkciju heurističke evaluacije, pribavljanjem dobijenih vrednosti. Potezi gde pobeđuju maksimiziranje igrača su dodeljeni sa pozitivnom beskonačnošću, dok su potezi koji dovode do pobede na minimiziranje igrača se dodeljuje sa negativnom beskonačnošću. Na trećem nivou, algoritam će izabrati, za svaki čvor, „najmanji“ od dete čvor vrednosti i dodeliti ga tom istom čvoru (npr. Čvor na levoj strani će izabrati minimu između „10“ i „+∞", dakle dodeliće sebi vredost „10“ ). Naredni korak, na drugom novou, sastoji se od izbora za svaki čvor u najveći od child node čvora vrednosti. Ponovo, vrednosti su dodeljene svakom roditelj čvor. Algoritam se dalje nastavlja ocenjivanjem najveće i najmanje vrednosti od dece čvorova naizmenično dok ne dostigne koren čvor gde se bira potez sa najvećom vrednošću (predstavljeni na slici sa plavom strelicom). To je potez koji igrač treba da u cilju minimiziranja na maksimalno moguću gubitak (loss).
Minimaks za pojedinačne odluke[uredi | uredi izvor]
Minimaks u lice neizvesnosti[uredi | uredi izvor]
Minimaks teorija je produžena do odluke gde ne postoji drugi igrač, ali gde posledice odluka zavise od nepoznatih činjenica. Na primer, odlučivanje za izglede troškova minerala koji će biti uzaludni ukoliko minerali ne postoje, ali će doneti značajno velike nagrade ako su prisutni. Jedan pristup je da se ovo posmatra kao igra protiv prirode, (pogledaj potez prirode (move by nature)), i koristeći sličan način razmišljanja kao Marfijev zakon, koristi pristup koji minimizuje maksimalni očekivani gubitak, koristeći iste tehnike kao i u dva igrača, nulto- suma igara.
Pored toga, expectiminimax tree su razvijeni, za igre za dva igrača u kojima je verovatnoća (na primer, kockice) je činilac.
Minimaks kriterijum u teoriji statističkog odlučivanja[uredi | uredi izvor]
U klasičnoj statističkoj teoriji donošenja (decision theory), imamo procenjivač (estimator) koji se koristi za procenu parametra (parameter) <math> \ theta \ u \ theta </ math >. Takođe pretpostavljamo funkciju rizika (risk function) , najčešće je navedena kao integral jedne funkcije gubitka (loss function). U tom okviru, zove se 'Minimaks' ako zadovoljava :
Alternativni kriterijum u donošenju teorijskog okvira je Bajesov procenjivač u prisustvu pre distribucije . Procenjivač je Bajesov ako minimizira prosečan rizik: :
Teorija donošenja odluka bazirana na ne-verovatnoći[uredi | uredi izvor]
Ključna karakteristika minimaksnoj odlučivanja je postojanje ne-verovatnoće: za razliku od odluka koje koriste očekivanu vrednost ili Očekivanu uslužnost, ona ne pravi pretpostavke o verovatnoće različitih ishoda, samo scenario analize šta su mogući ishodi. Stoga je robust promena u pretpostavkama, kao što ove druge tehnike donošenja odluka nisu. Razne ekstenzije ovog pristupa ne-verovatnoće postoje, posebno Minimaks žaljenje i Info-jaz teorija odluka.
Dalje, Minimaks zahteva samo redno merenje (da ishodi mogu biti uporedivi i rangirani), a ne interval“ merenja (da ishodi uključuju "koliko bolje ili glošije"), i vraća originalne podatke, koristeći samo uzorne ishode : zaključak o minimaks analizi je: "ovo je strategija Minimaks, gde je najgori slučaj (ishod), manje loš od bilo koje druge strategije". Upoređujući sa očekivanom vrednošću analize, čiji je zaključak oblika: ". Ovo strategija prinosi E(X)=n." Minimaks tako može da se koristi na rednim podataka, a može biti transparentniji.
Maximin u filozofiji[uredi | uredi izvor]
U filozofiji, termin "maximin" je često korišten u kontekstu John Rawls's A Theory of Justice, gde on referiše na (Rawls (1971, pp. 152)) u kontekstu različitih principa. Rawls je definisao ovaj princip kao korak koji zauzima socijalne i ekonomske neujednačnosti moraju da se organizuju. Drugim rečima, neunikatna distribucija se može koristiti kada maximizirano the minimalni. Benefiti onima koji imaju najmanje alokacije blagostanja dodeljivanja resursa. (Koji on referise kao "primarna dobra").[5][6]
Vidi još[uredi | uredi izvor]
Reference[uredi | uredi izvor]
- ^ Osborne, Martin J., and Ariel Rubinstein. A Course in Game Theory. Cambridge, MA: MIT, 1994. Print.
- ^ Von Neumann, J: Zur Theorie der Gesellschaftsspiele Math. Annalen. 100 (1928) 295-320
- ^ John L Casti (1996). Five golden rules: great theories of 20th-century mathematics – and why they matter. New York: Wiley-Interscience. str. 19. ISBN 978-0-471-00261-1.
- ^ Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd izd.), Upper Saddle River, New Jersey: Prentice Hall, str. 163—171, ISBN 0-13-790395-2
- ^ Arrow, "Some Ordinalist-Utilitarian Notes on Rawls's Theory of Justice, Journal of Philosophy 70, 9 (May 1973). pp. 245-263.
- ^ Harsanyi, "Can the Maximin Principle Serve as a Basis for Morality? a Critique of John Rawls's Theory, American Political Science Review 69, 2 (June 1975). pp. 594-606.
Literatura[uredi | uredi izvor]
- John L Casti (1996). Five golden rules: great theories of 20th-century mathematics – and why they matter. New York: Wiley-Interscience. str. 19. ISBN 978-0-471-00261-1.
Spoljašnje veze[uredi | uredi izvor]
- Hazewinkel Michiel, ur. (2001). „Minimax principle”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104.
- A visualization applet
- "Maximin principle" from A Dictionary of Philosophical Terms and Names.
- Play a betting-and-bluffing game against a mixed minimax strategy
- [1] The Dictionary of Algorithms and Data Structures entry for minimax.
- Minimax Arhivirano na sajtu Wayback Machine (24. mart 2015) (with or without alpha-beta pruning) algorithm visualization — game tree solving (Java Applet), for balance or off-balance trees.
- CLISP minimax game. (in Spanish)
- Maximin Strategy from Game Theory
- Minimax Tutorial with a Numerical Solution Platform







