Транспортни проблем

Транспортни проблем је један од проблема са поља операционих истраживања‎. Задатак је да се за дате спискове добављача и поручилаца неке робе организује транспорт тако да његове цене буду оптималне.

Опис решења[уреди | уреди извор]

Прво треба саставити матрицу транспортног проблема. То је матрица типа m × n, где је m број достављача а n број купаца. Свако поље (i,j) је намењено бележењу трговине између i-тог достављача и j-тог купца. Поред тога, свако поље матрице такође има и једно потпоље у којем се налази цена транспорта једне јединице трговине. Вредности a₁, ..., a_m представљају редом расположиве капацитете достављача, а b₁, ..., b_n потребе поручилаца. Нека цена транспорта за поље (i,j) буде C_i,j, а количина испоручене робе X_i,j.

Следећи корак је расподела транспорта тако да сви могући транспорти буду направљени тј. да збир испоручених јединица робе буде максималан.

\sum _{i=1}^{m}{\sum _{j=1}^{n}{X_{(i,j)}}}=max

Овај почетни распоред не мора бити оптималан. Два поступка за добијање ових распореда су метод најмањих цена и метод северозападног угла.

Након овога следи итеративни поступак оптимизације укупне цене транспорта. У матрици се тражи циклус који садржи тачно једно празно поље и непаран број попуњених поља. Правило за формирање циклуса је да се следећи елемент може само тражити по вертикали или по хоризонтали. Уколико је, почев од непопуњеног поља, збир цена транспорта изабраних поља са непарним индексом мањи него код поља са парним индексом прелази се на следећи корак, у супротном се тражи нови циклус.

По налажењу једног циклуса који одговара горенаведеном правилу о сумама вредности својих чланова, изабире се минимална вредност свих поља са парним индексом која циклус укључује. Ова вредност се потом одузима од свих поља са парним индексом у циклусу а додаје се сваком пољу са непарним индексом. Ово поређење се такође може вршити сумом свих елемената низа, с тим што знак за сваки следећи елемент алтернира. Да би услов био испуњен, сума мора бити мања од нуле. Као што је већ поменуто, непопуњено поље има индекс број 1, а смер даљег нумерисања није битан јер је број изабраних поља увек паран.

Кад се количина испоручене робе у неком пољу анулира, у том пољу остаје број нула и оно се не рачуна као непопуњено. Процес тражења циклуса и модификовања бројева у њему се понавља докле год постоје циклуси који задовољавају наведене услове.

Укупна цена транспорта у сваком моменту је сума производа вредности испоручене робе и цене транспорта сваког поља.

\sum _{i=1}^{m}{\sum _{j=1}^{n}{X_{(i,j)}\cdot C_{(i,j)}}}

Пример[уреди | уреди извор]

Рецимо да су дата три достављача, који редом располажу са 8, 5 и 6 пошиљки, и четири поручиоца са потражњама за 6, 4, 5 и 4 пошиљке. Ово је оптималан случај када је потражња једнака поунди. У пракси се чешће срећу тржиште оријентисано ка купцима, где је понуда већа од потражње и тржиште оријентисано ка продавцима, где је потражња већа од понуде.

Уз то је позната и матрица са ценама транспорта:

C={\begin{bmatrix}4&1&2&1\\1&3&5&1\\1&1&3&2\\\end{bmatrix}}

Тада ће матрица транспортног проблема, пре почетне расподеле, изгледати овако:	А након расподеле по методи северозападног угла, овако:

Након расподеле методом северозападног угла углавном је до коначног решења потребно више итерација него након расподеле методом најмањих цена. Овде је изабран метод северозападног угла да би се проблем кроз већи број итерација што боље представио.

Следећи корак је трагање за циклусом који одговара наведеном услову. Један такав је означен на слици испод. Пошто је δ = 1 - 4 + 1 - 3 < 0, у овом циклусу ће се у сваком „негативном“ пољу од испоручене робе одузети минимална вредност (у овом случају min{2, 6} = 2), а „позитивном“ пољу иста додати.

Нађени циклус C₂₁-C₁₁-C₁₂-C₂₂:	Резултат је следећи:

Итеративно се опет тражи циклус који задовољава услове. На слици испод је обележен циклус код кога је опет δ = 2 - 5 + 1 - 4 < 0, а минимална вредност min{3, 4} = 3:

Нађени циклус C₁₃-C₂₃-C₂₁-C₁₁:	Резултат:

Следи итеративно налажење даљих циклуса и њихова оптимизација:

Циклус C₃₁-C₃₃-C₁₃-C₁₁ δ = 1 - 3 + 2 - 4 < 0 min{1,2} = 1:	Циклус C₃₂-C₃₃-C₁₃-C₁₂ δ = 1 - 3 + 2 - 1 < 0 min{1,4} = 1:

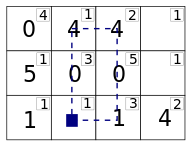
Циклус C₁₄-C₁₂-C₃₂-C₃₄ δ = 1 - 1 + 1 - 2 < 0 min{3,4} = 3:	Циклус C₂₄-C₂₁-C₃₁-C₃₄ δ = 1 - 1 + 1 - 2 < 0 min{5,1} = 1:

Коначни резултат

Може се приметити да се кроз итерације испоруке гомилају око поља где је цена транспорта најмања, што је сигнификатор оптимизације. У овом случају алгоритам је од почетне укупне цене транспорта C₁ = 6·4 + 2·1 + 2·3 + 3·5 + 2·3 + 4·2 = 61 дошао до цене C₂ = 5·2 + 3·1 + 4·1 + 1·1 + 2·1 + 4·1 = 24.

Специјални случајеви[уреди | уреди извор]

У пракси се може јавити и пар додатних услова који донекле мењају ток решавања.

Доставка од продавца i до наручиоца j није могућа: Постави се да цена доставке C_i,j буде ∞ и на то поље се не распоређује никаква доставка при почетном распоређивању.
Продавац i мора све да прода: Потреба за овим условом се јавља кад је понуда већа од потражње. Решење је да се дефинише још један наручилац коме треба тачна разлика између понуде и потражње, с тим да су цене доставке њему од свих достављача, сем достављача i једнаке нули, а цена доставке од достављача i до овог наручиоца ∞.
Наручилац j треба да буде намирен: Аналогно претходном случају, дефинише се још један продавац, који нуди разлику између потражње и понуде и постави се да су цене транспорта од њега до свих осталих наручилаца једнаке нули, а до j-ог ∞.

Спољашње везе[уреди | уреди извор]