Бенфордов закон
Бенфордов закон, такође познат и као закон прве цифре, тврди да је у многим списковима бројева који потичу из извора података из стварног живота, расподела водеће цифре прати специфичну, не-равномерну расподелу. Према овом закону, прва цифра је 1 готово трећину времена, веће цифре се појављују као водеће цифре са све мањом и мањом фреквенцијом, све до цифре 9 која се појављује као прва цифра мање него једном у двадесет случајева. Основа овог „закона“ јесте да су вредности које се добијају мерењима у стварном животу често расподељене логаритамски, због чега је логаритам вредности ових мерења, уопште говорећи, равномерно расподељен.
Испоставило се да је овај контраинтуитивни резултат применљив на најразличитије скупове података, укључујући рачуне за електричну енергију, уличне адресе, цене деоница, бројеве становника, стопе смртности, дужине река, физичке и математичке константе, и процесе које описују степени закони (односно закони у којима се зависност описује степеном функцијом, какви су веома чести у природи). Резултат важи без обзира на основу у којој изражавамо бројеве у смислу опадања фреквенција од мањих цифара ка већима, мада се конкретни постоци мењају.
Закон је назван по физичару Френку Бенфорду, који га је формулисао 1938, мада га је претходно изрекао Сајмон Њуком 1881.
Математички исказ[уреди | уреди извор]
Прецизније, Бенфордов закон тврди да се, уколико бројеве изражавамо у основи b (b ≥ 2), водећа цифра d (d ∈ {1, …, b − 1} ) појављује са вероватноћом
- P(d) = logb(d + 1) − logbd = logb((d + 1)/d).
Ова величина једнака је раздаљини између d и d + 1 на логаритамској скали.
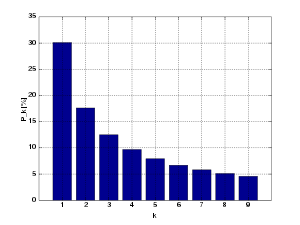
Конкретно, у основи 10, водеће цифре према Бенфордовом закону прате следећу расподелу, где је d водећа цифра и p је вероватноћа њеног појављивања:
| d | p |
|---|---|
| 1 | 30.1% |
| 2 | 17.6% |
| 3 | 12.5% |
| 4 | 9.7% |
| 5 | 7.9% |
| 6 | 6.7% |
| 7 | 5.8% |
| 8 | 5.1% |
| 9 | 4.6% |
Примене и ограничења[уреди | уреди извор]
1972. године, микроекономиста Хал Варијан, тада докторанд на Универзитету Калифорније у Берклију, је наговестио да би се закон могао користити за откривање могућих превара у социо-економским подацима који се подносе у прилог одлукама у области јавног планирања. Засновано на прихватљивој претпоставци да су људи који измишљају бројеве склони да своје цифре расподељују прилично равномерно, једноставно поређење расподеле фреквенције прве цифре у датим подацима са расподелом очекиваном у складу са Бенфордовим законом би требало да укаже на могуће неправилности. Водећи се овом идејом, Нигрини је показао да би се Бенфордов закон могао користити као индикатор рачуноводствених и превара у правдању трошкова.
Ограничења[уреди | уреди извор]
Међутим, у овим применама је потребно бити опрезан. Дату скуп података из стварног живота можда не подлеже закону, зависно од тога до које мере на расподелу бројева утиче природа саме категорије података.
На пример, неко би можда очекивао да би списак бројева који представља „бројеве становника села у Србији чија имена почињу на 'А'“ или пак „мале одштетне захтеве од осигурања“ подлегао Бенфордовом закону. Међутим, ако се испостави да је одређење „села“ „насеље са бројем становника између 300 и 999“, или да је одређење „малог одштетног захтева од осигурања“ „одштетни захтев вредности између 50 и 100 евра“, тада Бенфордов закон не би био применљив (макар не у свом основном облику) јер би извесни бројеви били искључени по одређењу скупа података.
Уопштења на цифре даље од прве[уреди | уреди извор]
Закон се може уопштити на цифре даље од прве. Посебно, вероватноћа наилажења на број који почиње извесном фиксираном ниском цифара n дата је као:
- .
На пример, вероватноћа да дати број почиње цифрама „314“ је log10(1+1/314). Помоћу овог резултата се може наћи вероватноћа да се одређена цифра налази на датој позицији унутар броја. На пример, вероватноћа да се цифра 2 налази на другој позицији (гледано слева) јесте
- .
Уколико фиксирамо ма коју од десет цифара, вероватноћа да ће n-та цифра броја бити једнака нашој цифри веома се брзо приближава ка 10% како n расте, односно, расподела n-те цифре се брзо приближава равномерној расподели када n → ∞.
Практичне примене Бенфордовог закона рутински користе више од само прве цифре.


