Грејев код
Рефлектовани бинарни код, такође познат као Грејев код по Френку Греју, је систем бинарних цифара у којем се две узастопне вредности разликују у само једном биту (Бинарне цифре ). Рефлектовани бинарни код је првобитно пројектован да спречи лажни излаз из електромеханичких прекидача. Данас, Грејеви кодови се широко користе да олакшају исправљање грешака у дигиталним комуникацијама, као што су дигиталне земаљске телевизије и неки кабловски системи.
Име[уреди | уреди извор]

Френк Греј, научник из Белових лабораторија, увео је термин рефлектовани бинарни код у његовој општепознатој апликацији из 1947. године, тврдећи да је код имао "још нема име"[1] Он је извео име из чињенице да је "могуће изградити од конвенционалних бинарних кодова као врста рефлексије процеса".
Код је касније назван по Греју од стране других који су га користили. Две различите 1953 патент апликације користе Грејев код као алтернативно име за "рефлектовани бинарни код";[2][3] један од ових такође наводи "минимална грешка кода" и "циклична пермутација кода" међу именима .[3] 1954 патент апликација се односи на " звоно телефона Грејевог кода ".[4]
Мотивација[уреди | уреди извор]
Многи уређаји указују на позицију отварања и затварања прекидача. Ако тај уређај користи природне бинарне кодове, позиције 3 и 4 су једна до друге али сва три бита бинарне представе се разликују:
| Децимални | Бинарни |
|---|---|
| ... | ... |
| 3 | 011 |
| 4 | 100 |
| ... | ... |
Проблем са природним бинарним кодовима је да ће, са физичким, механичким прекидачима, врло ретко да промене стање тачно синхронизовано. На прелазу између два стања, приказаним изнад, сва три прекидача мењају стање. У кратком периоду док се сви мењају, прекидачи ће прочитати неку лажну позицију. Чак и без прекидача, транзиција може да изгледа 011 — 001 — 101 — 100. Када су прекидачи у позицији 001, посматрач не може рећи да ли је стварна позиција 001, или је транзиционо стање између друге две позиције. Ако се извршен рад напаја унутар секвенцијалног система, вероватно преко комбинационе логике, онда ће секвенцијални систем да складишти лажну вредност.
Рефлектовани бинарни код решава овај проблем тако што ће променити само један прекидач у једном тренутку, тако да никада не постоји двосмисленост позиције,
| Децимални | Бинарни | Греј | Греј као Децимални |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 001 | 1 |
| 2 | 010 | 011 | 3 |
| 3 | 011 | 010 | 2 |
| 4 | 100 | 110 | 6 |
| 5 | 101 | 111 | 7 |
| 6 | 110 | 101 | 5 |
| 7 | 111 | 100 | 4 |
Примећује се да стање 7 може да пређе у стање 0 са само једном променом прекидача. То се назива "циклично" власништво Грејевог кода. У стандардном Грејевом кодирању најмањи значајни бит прати шаблон који се понавља искључено 2 укључено, 2 искључено (...11001100...); следећа цифра образац искључено 4 укључено, 4 искључено и тако даље.
Више формално, Грејев код је код преписан свакоме од скупа целих бројева, или сваком члану циркуларне листе, реч симбола као што свака два суседна кода речи припадају једном симболу. Ови кодови су такође познати као једно-раздељински кодови, рефлектујући Хамингово растојање од 1 између суседних кодова. Тамо може бити више од једног Грејевог кода за дату дужину речи, али термин је прво употребљен на одређени бинарни код за не-негативне целе бројеве, Бинарно рефлектујући Грејев код, или БРГК, тробитна верзија која је приказана изнад.
Историја и практична апликација[уреди | уреди извор]
Рефлективни бинарни код је био примењен на математичку слагалицу пре него што је постао познат инжењерима. Француски инжењер Емил Баудот је користио Грејев код у телеграфији 1878.[5] Он је примио француски орден Легију части за свој рад. Грејев код се понекад преписује неправилно,,[6]за Елишу Греј ( на принципима модулације импулсног кода, К. В. Катермол,[7] на пример).
Франк Греј, који је постао познат за стварање сигналног метода који се користи за компатибилни телевизор у боји, измислио је метод да претвори аналогне сигнале у рефлективне групе бинарних кодова користећи апарат заснован на електронским цевима. Метода и апарати су били патентирани 1953 и име Греј је остало у кодовима. "Импулсна кодна модулациона цев", направа коју је Греј патентирао је направљена од стране Рејмонда Б. Сеарса од Бела Лабса, радећи са Грејем и Вилијамом М. Гудолом, који је дао заслуге Греју за идеју рефлективног бинарног кода. [8]
Употреба његових истоимених кодова за које је Греј највише био заинтересован била је да смањи ефекат грешке у разговору аналогних сигнала до дигитализације; његови кодови се још увек користе данас за ову сврху и друге.
Позициони кодери[уреди | уреди извор]


Грејев код се користи у позицији кодера (Линеарног кодера и ротационог кодера), у жељи да се једноставно бинарно кодира. Овим се избегава могућност да, када се неколико битова мења у бинарној репрезентацији под углом, а процена ће резултирати од неког од битова промене пре других. Првобитно, образац је био електрично проводљив, подржан (у ротационом кодеру) изолационим диском. Свака стаза је имала свој стационарни метални контакт са опругом; још један контакт који је направио везу са узроком. Тај заједнички контакт је повезан узроком на било који од контаката стазе на одмору проводног обрасца. Међутим, клизни контакти се похабају и потребно им је одржавање, које фаворизује оптичке кодере.
Без обзира на усклађивању контаката, и тачност узрока, природни-бинарни код ће имати грешке на одређеним позицијама диска, јер је немогуће да се сви битови промене у исто време док се диск окреће. Исто важи и за оптичке кодере; Прелази између нетранспарентних и транспарентних се не могу истовремено одвијати за одређене тачне позиције. Ротациони кодери користе цикличну природу Грејевог кода, јер узастопни положаји секвенце се разликују за само један бит. То значи да, за транзицију из стања А у стање B, временски несклад може само да утиче када се А → Б транзиција јавља, пре него убацивањем једног или више (до n - 1 за N-битну кодну реч) лажну међу стањима, како би дошла ако се користи стандардни бинарни код.
Ханојска кула[уреди | уреди извор]
Бинарни огледи Грејевог кода могу се користити као водич решења за проблем Ханојске куле, као и класичне кинеске слагалице прстенова, секвенцијалне механичке слагалице механизма.[6]Такође формира Хамилтонов циклус на хиперкубу, где се сваки бит види као једна димензија.
Генетски алгоритми[уреди | уреди извор]
Због својства Хамингове удаљености од Грејевог кода, они се понекад користе у генетским алгоритмима. Они су веома корисни у овој области, јер мутације у коду омогућавају углавном постепене промене, али повремено промена једног бита може изазвати велики скок и довести до нових својстава.
Карноова карта[уреди | уреди извор]
Грејеви кодови се такође користе у означавању оса Карноове карте.[9]
Исправка грешке[уреди | уреди извор]
У модерној дигиталној комуникацији, Грејеви кодови играју важну улогу у исправљању грешке. На пример, у дигиталним модулационим шемама као што је КАМ где се подаци обично преноси у симболима од 4 бита или више, сигнали констелациског дијаграма су уређени тако да се обрасци битова преносе од сазвежђа суседних тачака разликујући се само за један бит. Комбиновањем са раном корекцијом грешака способном да исправља једнобитне грешке, могуће је да пријемник исправи све грешке преноса које узрокују да сазвежђа указују на одступања у области суседне тачке. То чини преносни систем мање подложан буком
Комуникација између домена сата[уреди | уреди извор]
Дигитални Логички дизајнери користе Грејев код интензивно за доношење мулти-битних броја информација између синхрони логике која послује на различитим часовним фреквенцијама. Логика се сматра да послује у различитим "доменима сата". То је основа за пројектовање великих чипова који раде са много различитих фреквенција часовника.
Бројачи Грејевог кода и аритметика[уреди | уреди извор]
Типична употреба бројача Грејевог кода гради ПУПВ (први-у, први-ван) међумеморију податка, који читају и пишу портове који постоје у различитим доменима сата. Улазни и излазни бројачи унутар тих дуалних портова ПУПВ су често чувани користећи Грејев код за спречавање неважећих прелазних стања од заробљавања, када датотека прелази домен сата.[10] Ажурирани читани и писани показивачи треба да буду усвојени од домена сата када се мењају, да би могли да прате ПУПВ празан и пуноправни статус у свакој области. Сваки бит од показивача је одабран не-детерминистички за тај трансфер домена сата. Дакле, за сваки бит, било стара вредност или нова вредност се пропагира. Дакле, ако више од једног бит у мулти-битни показивач се мења у тренутку узорковања, као "погрешна" бинарна вредност (ни нова ни стара) може бити пропагирана. Гарантујући само један бит може да се мења, Грејев код гарантује да једине могуће одобрене вредности су нове или старе више-битне вредности. Типични Грејеви стартне две дужине се користе.
Понекад дигитални аутобуси у електронским системима се користе за пренос количина које се само могу повећати или смањити један по један, на пример, излаз за догађај који се догодио између домена сата или на дигитално-аналогном конвертору. Предност Грејевог кода у овим апликацијама је да разлике у пропагирању одлагања многих проводника који представљају делове кода не могу изазвати примљене вредности пролазећи кроз стања која су ван Грејевих секвенци. Ово је слично ка предностима Грејевог кода у изградњи механичких кодера, међутим, извор Грејевог кода је електронски бројач у овом случају. Сам бројач мора рачунати у Грејевом код, или ако је у супротности у бинарном онда излазна вредност од бројача мора бити измерена након што је претворена у Грејев кода, јер када је вредност претворена из бинарног у Грејев код, могуће је да ће разлике у времену доласка бинарних битова података у бинарну Грејеву конверзију кола значити да је број могао укратко проћи кроз стања која су дивља у редоследу. Додавање регистара сата после склопа који претвара број вредност Грејевог кода може увести сат циклуса кашњења, па рачунање директно у Грејевом коду може бити корисно. Бројач Грејевог кода је патентиран 1962 УС3020481 и било је много других од тад. У новије време бројач сивог кода може бити имплементиран као стање машине у Верлиогу. Да би се спровео следећи број вредности неопходно је да се користи комбинована логика која ће прирасти тренутну бројевну вредност која се складишти у Грејевом коду. Вероватно најочигледнији начин да повећате цифру Грејевог кода је да га претворити у обичан бинарни код, додајте један томе са стандардним бинарним додатком, а затим претворите резултат назад у Грејев код. О овом приступу је разговарано у новинама 1996. године [11], а потом је и патентирано од стране неког другог 1998 УС5754614 . Друге методе бројање у Грејевом коду се расправљају у извештају Р. В. Дорана, укључујући и узимање излаза из првих реза флип флопса у бинарном бројачу таласања .[12]
Можда је најчешћи електронски бројач са "само једним промена бита у времену " имовина је Џонсонов бројач .
Конструкција н-битног Грејевог кода[уреди | уреди извор]


Бинарне рефлексије Грејевог кода листа за н битова може бити рекурзивно генерисана из листе за н-1 битова по рефлектовању листе ( тј листање ставки обрнутим редоследом ), надовезивањем оригиналних листи са обрнуте листе, префикси уноса у оригинални списак са бинарном цифром 0, а затим фиксирање ставке у рефлектујућу листу са бинарном цифром1. На пример, генерисањем н=3 листе од н=2 листе :
| 2-битна листа: | 00, 01, 11, 10 | |
| Рефлектовани: | 10, 11, 01, 00 | |
| Префикс старог уноса са 0: | 000, 001, 011, 010, | |
| Префикс новог уноса са 1: | 110, 111, 101, 100 | |
| Спојени: | 000, 001, 011, 010, | 110, 111, 101, 100 |
Један бит Грејевог кода је Г1 = ( 0, 1 ) . Ово се може посматрати као изграђено рекурзивно као што горе нула-битни Грејев код Г0 = {Λ} се састоји од једног уласка нулте дужине. Овај учестали процес стварања Гн+1 оd Гн даје следеће особине стандардног рефлектујућег кода јасним:
- Гн је пермутација бројева 0, .., 2н-1 . ( Сваки број се појављује тачно једном у листи. )
- Гн је уграђен као прва половина од Гн+1
- Стога кодирање је стабло, у смислу да се једном бинарни број појављује у Гн, појављује се у истом положају у свим дужим листама; тако да има смисла говорити о рефлексивној вредности броја Грејевог кода Г(м) = м- ти рефлектујући Грејев код, рачунајући од 0 .
- Сваки унос у Гн разликује се само по једном биту од претходног уноса. (Хамингова удаљеност је 1)
- Последњи унос у Гн разликује се само по једном биту од првог уноса (Код је цикличан)
Ове карактеристике указују на једноставан и брз начин превођења бинарних вредности у одговарајући Грејев код. Сваки бит је ротиран ако је следећи већи бит улазне вредности постављен на један. Ово се може извршити паралелно од битне-смене и искључиво - или руковањем ако су доступни : н-ти грејев код се добија израчунавањем
Сличан поступак се може користити за извођење супротних превода, али рачунање сваког бита зависи од израчунате вредност следећег вишег бита тако да се не може вршити паралелно. Под претпоставком да је gи бит i-тог Грејевог кода (g0 је највише значајан бит), и bи је бит i-тог бинарног кода (b0 је највише значајан бит) обрнут превод може дати рекурзивно: b0=g0 и би=gи . Алтернативно, декодирање Грејевог мода у бинарни број се може описати као префикс збира битова у Грејевом коду, где сваки појединац операције у префиксу суме се врши по модулу два.
Да итеративно изградите бинарно-рефлектујући Грејев код, корак 0 почните са код0 = 0, а на корак i>0 нађи позицију бута најмање тежине 1 у бинарној заступљености од и померите бит на претходни положај кодаи-1 да бисте добили следећи код коди . Позиције битова почиње са 0, 1, 0, 2, 0, 1, 0, 3, ... ( секвенца А007814 у ОЕИС) . Погледајте пронађи први сет за ефикасне алгоритме за израчунавање ове вредности .
Претварање до и од Грејевог кода[уреди | уреди извор]
Следеће функције у C претварају између бинарних бројева и њихових повезаних Грејевих кодова. Иако може изгледати да Греј-на-бинарни конверзија захтева да се са сваким битом рукује један по један, брже алгоритми постоји . [13]
/*
* Ова функција конвертује непотписани бинарни
* број рефлектује бинарни Грејев код.
*
* Оператор >>је смена десно. Оператор ^ је искључив или.
*/
unsigned int binaryToGray(unsigned int num)
{
return num ^ (num >> 1);
}
/*
* Ова функција конвертује непотписани бинарни
* број рефлектује бинарни Грејев код.
* Сваки бит Грејевог кода искључиво изводе набројане са свим
* више значајних битова.
*/
unsigned int grayToBinary(unsigned int num)
{
unsigned int mask;
for (mask = num >> 1; mask != 0; mask = mask >> 1)
{
num = num ^ mask;
}
return num;
}
/*
* Ефикаснији верзија за Грејеве кодове од 32 или мање бита.
*/
unsigned int grayToBinary32(unsigned int num)
{
num = num ^ (num >> 16);
num = num ^ (num >> 8);
num = num ^ (num >> 4);
num = num ^ (num >> 2);
num = num ^ (num >> 1);
return num;
}
Специјални типови Грејевих кодова[уреди | уреди извор]
У пракси, "Грејев код" готово увек се односи на бинарни - рефлектујући Грејев код ( БРГК ) . Међутим, математичари су открили и друге врсте Грејевог кода. Као БРГК, сваки се састоји од листе речи, где свака реч се разликује од следеће у само једној цифри ( свака реч има Хамингову удаљеност 1 од следеће речи ) .
н-арни Грејев код[уреди | уреди извор]
|
Постоје многе специјализоване врсте Грејевих кодова осим у бинарном-рефлектујућем Грејевом коду . Један такав тип Грејевог кода је н-арни Грејев код, такође познат као не- логички Грејев код . Као што само име каже, овај тип Грејевог кода користи не - логичку вредност у својим кодирањима.
На пример, троструки Грејев код ће користити вредности {0, 1, 2 } . ( н, к ) -Грејев код је н-арни Грејев код са к цифрама [14]. Секвенца елемената у ( 3, 2 ) -Грејевом коду је : { 00, 01, 02, 12, 10, 11, 21, 22, 20 } . ( н, к ) -Грејев код може бити конструисан рекурзивно, као БРГК, или може бити конструисан итеративно . Алгоритам за итеративно генерисање ( н, к) -Грејевог кода је представљен ( у Ц) :
// улази: база, бројеви, вредности
// излаз: греј
// Претварање вредности на грејевим кодовима са датом базом и цифром.
// Итеративно путем низа вредности ће резултирати у низу
// грејев код у којем само једна цифра се мења у времену.
void to_gray(unsigned base, unsigned digits, unsigned value, unsigned gray[digits])
{
unsigned baseN[digits]; //Залихе обичних база Н бројева, једна цифра по уносу
unsigned i; // Променљива петља
// Ставите нормалну базуН броја у базу низа. На базу 10, 109
// биће складиштено као [9,0,1]
for (i = 0; i < digits; i++) {
baseN[i] = value % base;
value = value / base;
}
// Претвори нормалан базуН броја у еквивалентан грејев код. Напоменути да
// петља почиње у најзначајније цифре и пада.
unsigned shift = 0;
while (i--) {
// Цифре греја су померене доле сумом већих
// бројеви.
gray[i] = (baseN[i] + shift) % base;
shift = shift + base - gray[i]; // Претварање вредност на грејев код са датом базом и цифрама. Одузимање од базе, такав помак је позитиван
}
}
// примери
// улаз: вредности = 1899, base = 10, digits = 4
// излаз: базаН[] = [9,9,8,1], gray[] = [0,1,7,1]
// улаз: вредност = 1900, base = 10, digits = 4
// излаз: базаН[] = [0,0,9,1], gray[] = [0,1,8,1]
Постоје и други алгоритми Грејевог кода за ( н, к) -Грејев код .( н, к ) -Грејев код произведен од стране алгоритма изнад увек је цикличан; неки алгоритми, као што су Гуан, [14] немају ову особину када је к непарно. С друге стране, док само једну цифру истовремено мењамо са овим методом, она може променити обавијањем ( петља је од н-1 до 0 ) . У Гуан алгоритма, рачун наизменично расте и пада, тако да је нумеричка разлика између две цифре грејевог кода увек један .
Греј кодови нису јединствено дефинисани, јер је пермутација колона таквог кода као сиви код. Наведени поступак производи код у коме је мањи значај цифре, чешће се мења, што је слично са уобичајеним поступцима пребројавања .
Погледајте такође попречни бинарни систем бројева, варијанта троструког бројевног система у којем највише 2 цифре мењају свој прираст, јер сваки пораст може да се уради са највише једном цифром ношења операције .
Балансирани Грејев код[уреди | уреди извор]
Иако је бинарни рефлектујући Грејев код користан у многим сценаријима, није оптималан у неким случајевима због недостатка " униформности ".[15] У избалансираним Грејевим кодовима, број промена у различитим позицијама координате је што је ближе могуће. Да би то прецизирали, нека буде Г Р-арни комплетан циклус Греја имајући транзицију секвенце бк; у транзицији тачака (Спектра) од Г су прикупљани цели бројеви који су дефинисани
Грејев код је једнак или једнако избалансиран ако његове транзиционе тачке су све једнаке, у том случају имамо за све к. Јасно, када је , такви кодекси постоје само ако је н јачине 2. У супротном, ако је н не дели равномерно, могуће је изградити добро уравнотежене кодове где је свака транзиција датотеке или или . Грејеви кодови могу такође бити експоненцијално уравнотежени ако све њихове транзиције тачака су суседне јачине два, и такви кодекси постоје за сваку јачину два . [16]
На пример, уравнотежен 4 -битни Грејев код има 16 прелаза, који се могу равномерно распоредити у све четири позиције (четири прелаза на позицији ), што га чини равномерно избалансираним :
0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1
док уравнотежени 5 - битни Грејев кода има укупно 32 прелаза, који се не могу равномерно распоредити међу позицијама. У овом примеру, четири позиције имају по шест прелаза, и једна има осам : [15]
1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 1
Ми ћемо сада показати конструкцију за добро избалансиран бинарни Грејев код који нам омогућава да генеришемо Н цифре избалансираног Грејевог кода за свако н [17] Основни принцим је да се индуктивно коструише (н+2) број Грејевог кода Г' - даје н-цифрени Грејев код Г на такав начин да је избалансирана имовина сачувана. Да би ово урадили, ми сматрамо партиције на Г=г0,......г2н-1 у паран број Л, не празних блокова у облику
где , и (mod ). Ова подела индукује -цифре Грејевог кода дате од
Ако дефинишемо умножену транзицију да је број пута у којој се цифра у позицији и мења између узастопних блокова у партицији, затим за ( н + 2 ) -број Грејевог кода изазвана од ове поделе транзиције спектра је
Деликатан део ове конструкције је да пронађе адекватну поделу уравнотеженог Грејевог кода Н-цифри који суизазвали код да остане избалансиран. Уједначени кодови се могу наћи када је и , а ова конструкција може бити продужена до Р -арног случаја.[17]
Монотони Грејев код[уреди | уреди извор]
Монотони кодови су корисни у теорији интерконекције мрежа, посебно за минимизирање дилатације за линеарне низова процесора.[18] Ако дефинишемо тежину бинарног низа да је број 1с у низу, онда иако ми јасно не може имати Грејев код са строго повећаном тежином, можемо желети да приближимо то тако што код поделимо у две суседне тежине пре него што стигну следећи .
Можемо да формализујемо концепт монотоног Грејевог кода на следећи начин: размотрити поделу хиперкуба Qn = ( Vn, En ) у нивое темена који имају једнаку тежину, односно
за . Ови низови задовољавају . Нека буде подграфикон од изазван од , и нека буде ивица у. Монотони Грејев код је онда Хамилтонов пут у тако да кад год дође пре у стази, онда је .
Елегантна изградња монотоног Грејевог кода са Н-цифрама за свако н заснива се на идеји рекурзивним грађење под стазе дужине имају ивице у.[18]Ми дефинишемо , кад год или , и
другачије. Овде, Пи је прикладно дефинисана пермутација односи се на путањи П са својим координатама пермутованим од пи. Ови путеви доводе до два монотона Грејева кода Н-цифара и дата од
Избор пи_н који обезбеђује да ови кодови буду заиста Грејеви кодови испоставља се да је . Првих неколико вредности су приказани у табели испод.
| j = 0 | j = 1 | j = 2 | j = 3 | |
|---|---|---|---|---|
| н = 1 | 0, 1 | |||
| н = 2 | 00, 01 | 10, 11 | ||
| н = 3 | 000, 001 | 100, 110, 010, 011 | 101, 111 | |
| н = 4 | 0000, 0001 | 1000, 1100, 0100, 0110, 0010, 0011 | 1010, 1011, 1001, 1101, 0101, 0111 | 1110, 1111 |
Ови Монотони Грејеви кодови могу бити ефикасно спроведени на такав начин да сваки наредни елеменат се генерише у О(н) времену. Алгоритам је најлакше описати коришћењем корутине.
Монотони кодови имају једну занимљиву везу са Ловасовом претпоставком, у којем се наводи да сваки повезан највиши - прелазан граф садржи Хамилтонов пут. "Средњи ниво " подграф К_ { 2н + 1 } ( н) највиши - прелазан (то јест, његова аутоморфна група је прелазана, тако да сваки чвор има исто " локално окружење " " и не може се разликовати од других, јер можемо поново означити координате као бинарне цифре да добијемо аутоморфизам) и проблем налажења Хамилтоновог пута у овом подграфу се назива " средњи ниво проблема ", која може да пружи увид у више општој претпоставци. На питање је потврдно одговорено за н<15, а претходна конструкција за монотоне кодове осигурава Хамилтонов пут дужине најмање 0.839Н где је Н број чворова у средини нивоа подграфа.[19]
Бекет-Грејев код[уреди | уреди извор]
Друга врста Грејевог кода, Бекет - Грејев код, назван је за ирског драмског писца Семјуел Бекет-а, који је био заинтересован за симетрију. Његова представа " Дуал " има четири глумца и подељен је на шеснаест временских периода. Сваки период се завршава са једним од четири глумаца који улази на или излази са бине. Представа почиње са празном бином, а Бекет желе да се сваки подскуп актера појави на бини тачно једанпут.[20] Јасан скуп глумаца тренутно на сцени може се представити са 4- битним бинарним Грејевим кодом. Бекет, међутим, ставља додатна ограничење на сценарију : жели да глумци улазе и излазе тако да глумац који је био на сцени најдуже буде тај који следећи излази. Глумци би тада могли бити представљен и тако да су први у, први из реда, тако да ( од актера на бини ) глумац који нема ред увек буде онај који је први пут добио ред.[20] Бекет је био у стању да пронађе Бекет - Грејев код за његову игру, и заиста, исцрпан попис свих могућих секвенци открива да такав број не постоји за н = 4. Познато је данас да такви кодекси постоје за н = 2, 5, 6, 7, 8 и, и не постоје за н = 3 или 4. Пример 8 - битни Бекет - Грејев код се може наћи у Кнутхе уметности компјутерског програмирања[6] Према Савади и Вонгу, за претраживање простор за н = 6 могу бити истражени у 15 сати, а више од 9.500 решења за случај Н = 7 су пронађени.[21]
Змија у кутији код[уреди | уреди извор]
Змија у кутији кодови, или змија, су секвенце чворова побуђених путева у Н - димензионалном графикону хиперкуба, и калем - ин-тхе- бок кодови, или калемови, су секвенце чворова намерних циклуса у Хиперцубе. Гледано у Грејевом коду, ове секвенце имају особину да буду у стању да открију било који један -бит кодирања грешке. Кодове овог типа је први описао В. Х. Каутз у касним 1950-им;[22] Од тада, било је много истраживања на проналажењу кода са највећим могућим бројем шифри за дату димензију хиперкуба.
Једна трака Грејевог кода [уреди | уреди извор]
Још једна врста Грејевог кода је појединачна трака Грејевог кода (СТГЦ) откривена од стране Спединга[23] и рафинирани од стране Хилтгена, Патерсона и Брандестинија у " Појединачној траци Грејевог кода "(1996).[24][25] СТГЦ је циклична листа П-а, јединствених бинарних кодирања дужине н да такве две узастопне речи се разликују у тачно једној позицији и када је листа испитивана као П×Н матрица, свака колона је циклично померена првој колони.[26]
Назив потиче од њихове употребе са ротационим кодерима, где је велики број нумера био схваћен контактима, што је резултирало за сваки излазу 0 или 1. Да бисте смањили буку због различитих контаката не пребацујући у истом моменту, једна пожељно поставља трагове тако да излазни подаци од контаката су Грејеви кодови. Да бисте добили високе угаоне тачности, потребно је доста контаката ; у циљу постизања најмање 1 прецизности ступњева, потребно најмање 360 различитих ставова по револуцији, што захтева минимум 9 битова података, а тиме и исти број контаката .
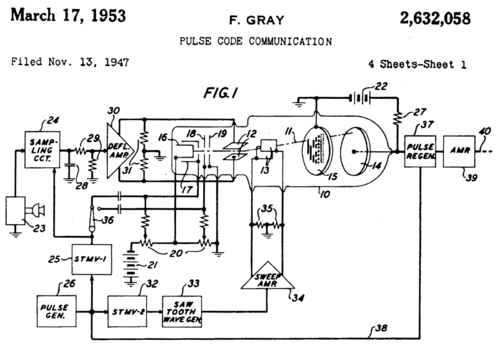
Ако су сви контакти постављени на истим угаоним позицијама, 9 стаза је потребно да се добије стандардни БРГК са најмање 1 тачношћу степена. Међутим, ако произвођач помера контакт на друге угаоне позиције ( али у истој удаљености од центра осовине ), а затим одговарајуће " звоно " треба да се ротира истим углом да би дали исти излаз. Ако најзначајнији бит ( унутрашњи прстен на слици 1 ) довољно ротира, тачно одговара следећем прстену напољу. Пошто оба прстена су тада идентична, унутрашњи прстен може се искључити, а сензор за тај прстен пресели у преостали, идентичан прстен ( али огранак под тим углом од другог сензора на тај прстен ) . Та два сензора на једном прстену праве квадратне кодере. То смањује број нумера за " 1 степен резолуције " угаоног кодера до 8 нумера. Смањење броја нумера додатно не може бити учињено са БРГК .
Дуги низ година, Торстен Силке[27] и други математичари су веровали да је било немогуће да кодирају положај на једној стази тако да узастопне позиције се разликују од само једног сензора, осим за 2 - сензор, 1 - трака квадратног кодера. Дакле, за апликације где би 8 трака било превише гломазно, људи су користили појединачну-траку инкременталних енкодер ( куадратурни кодери ) или 2 - стаза " квадратних кодера + референтни ниво" кодера
Напомена Спединг је, међутим, регистровао патент 1994. године са неколико примера који показују да је могуће .[23] Иако није могуће разликовати 2н позиције са н сензорима на једној стази, могуће је разликовати близину многих од њих. На пример, када је н само јачине 2, Н сензори могу разликовати 2н - 2н позиције .[28] Хилтен и Патерсон су објавило рад 2001. године излажући Појединачну-траку Грејевог кода са тачно 360 угаоних позиција, изграђених користећи 9 сензора.[25] Пошто је тај број већи од 28 = 256, више од 8 сензори су потребни за било који код, иако БРГК је могао да разликује 512 позиција са 9 сензора. СТГК за п = 30 и н = 5 се овде репродукује :

| Угао | Код | Угао | Код | Угао | Код | Угао | Код | Угао | Код |
|---|---|---|---|---|---|---|---|---|---|
| 0° | 10000 | 72° | 01000 | 144° | 00100 | 216° | 00010 | 288° | 00001 |
| 12° | 10100 | 84° | 01010 | 156° | 00101 | 228° | 10010 | 300° | 01001 |
| 24° | 11100 | 96° | 01110 | 168° | 00111 | 240° | 10011 | 312° | 11001 |
| 36° | 11110 | 108° | 01111 | 180° | 10111 | 252° | 11011 | 324° | 11101 |
| 48° | 11010 | 120° | 01101 | 192° | 10110 | 264° | 01011 | 336° | 10101 |
| 60° | 11000 | 132° | 01100 | 204° | 00110 | 276° | 00011 | 348° | 10001 |
Свака колона је циклично померање прве колоне, и из било ког реда у следећи ред само је једаn бит промене.[29] Појединачна-стаза природе ( попут кода ланац) је корисна у изради ових точкова (у поређењу са БРГК ), као што је потребна само једна стаза, чиме се смањује њихова цена и величина. Грејев код природе је користан ( у поређењу са ланцем кодова, који се називају де Бруијне секвенце), само један сензор ће променити у било ком тренутку, тако да неизвесности у току транзиције између два дискретна стања ће само бити плус или минус једне јединице угаоног мерног уређаја способног за решавање.[30]
Дводимензионални Грејев код[уреди | уреди извор]

Дводимензионални Грејеви кодови се користе у комуникацији како би се смањио број бит-них грешака у Квадратури амплитудних модулација суседних тачака у Констелациском дијаграму . У типичном кодирању хоризонталних и вертикалних суседних дијаграма тачака разликују се по једном биту, и дијагоналне суседне тачке разликују се по 2 бита . [31]
Грејева изометрија[уреди | уреди извор]
Бијективно мапирање{ 0 ↔ 00, 1 ↔ 01, 2 ↔ 11, 3 ↔ 10 } успоставља изомерију између метричког простора на крајњем пољу са метричким датим од Хаминговог растојања и метрички простор током крајњег прстена (уобичајено модул аритметике) са метричким датим од Лееовог растојања. Мапирање је прикладно проширено на изомерни Хамингов простор и . . Њен значај лежи у успостављању преписке између " добрих " врености, али не мора да иде линеарним кодексима, као Грејеве- мапе прстенастих линеарних кодова из.[32][33]
Види још[уреди | уреди извор]
- Линеарни повраћај регистроване смене
- Де-Бруин редослед
- Гилијамов код
- Стеинхаус-Џонсон-Тротеров алгоритам, алгоритам који генерише Грејеве кодове за факторски систем бројева
Референце[уреди | уреди извор]
- ^ F. Gray.
- ^ J. Breckman.
- ^ а б E. A. Ragland et al.
- ^ S. Reiner et al.
- ^ Pickover, Clifford A. (2009). Недостаје или је празан параметар
|title=(помоћ) - ^ а б в Knuth, Donald E. "Generating all n-tuples."
- ^ Cattermole, K. W. (1969). Недостаје или је празан параметар
|title=(помоћ) - ^ Goodall, W. M. (1951). Недостаје или је празан параметар
|title=(помоћ) - ^ Wakerly, John F (1994). Недостаје или је празан параметар
|title=(помоћ) - ^ "Synchronization in Digital Logic Circuits by Ryan Donohue
- ^ Mehta, H.; Owens, R.M. & Irwin, M.J. (1996), Some issues in gray code addressing, in the Proceedings of the 6th Great Lakes Symposium on VLSI (GLSVLSI 96), IEEE Computer Society. pp. 178.
- ^ The Gray Code by R. W. Doran
- ^ Henry Gordon Dietz. "The Aggregate Magic Algorithms: Gray Code Conversion"
- ^ а б Guan, Dah-Jyh (1998). „Generalized Gray Codes with Applications”. Proc. Natl. Sci. Counc. Repub. Of China (A). 22. CiteSeerX 10.1.1.119.1344
 .
.
- ^ а б Bhat, Girish S.; Savage, Carla D. (1996). „Balanced Gray codes”. Electronic Journal of Combinatorics. 3 (1): R25. doi:10.37236/1249.
- ^ Suparta, I. N. (2005). Недостаје или је празан параметар
|title=(помоћ) - ^ а б M. Flahive and B. Bose (2007). Недостаје или је празан параметар
|title=(помоћ) - ^ а б C. D Savage and P. Winkler (1995). Недостаје или је празан параметар
|title=(помоћ) - ^ C. D Savage (1997). Недостаје или је празан параметар
|title=(помоћ) - ^ а б Goddyn, Luis (1999).
- ^ Sawada, J.; Wong, D. (2007). Недостаје или је празан параметар
|title=(помоћ) - ^ Kautz, W. H. (1958). Недостаје или је празан параметар
|title=(помоћ) - ^ а б NZ 264738, Spedding, Norman Bruce, "A position encoder", published 1994 A claim is at http://www.winzurf.co.nz/Single_Track_Grey_Code_Patent/Single_track_Grey_code_encoder_patent.pdf
- ^ Hiltgen, Alain P.; Paterson, Kenneth G.; Brandestini, Marco (1996). Недостаје или је празан параметар
|title=(помоћ) - ^ а б Hiltgen, Alain P.; Paterson, Kenneth G. (септембар 2001). Недостаје или је празан параметар
|title=(помоћ) - ^ Etzion, Tuvi; Schwartz, Moshe (1999). Недостаје или је празан параметар
|title=(помоћ) - ^ Torsten Sillke.
- ^ Etzion, Tuvi; Paterson, Kenneth G. (мај 1996). Недостаје или је празан параметар
|title=(помоћ) - ^ Ruskey, Frank; Weston, Mark (June 18, 2005). Недостаје или је празан параметар
|title=(помоћ) - ^ Alciatore, David G.; Histand, Michael B. (1999). Недостаје или је празан параметар
|title=(помоћ) - ^ comp.dsp | Gray code for QAM
- ^ Marcus Greferath (2009). Недостаје или је празан параметар
|title=(помоћ) - ^ Encyclopedia of Mathematics
Литература[уреди | уреди извор]
- Black, Paul E. Gray code. 25 February 2004. NIST.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). „Section 22.3. Gray Codes”. Numerical Recipes: The Art of Scientific Computing (3rd изд.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Архивирано из оригинала 11. 08. 2011. г. Приступљено 21. 11. 2015.
- Savage, Carla (1997). „A Survey of Combinatorial Gray Codes”. SIAM Rev. 39 (4): 605—629. Bibcode:1997SIAMR..39..605S. JSTOR 2132693. S2CID 6375360. doi:10.1137/S0036144595295272. Архивирано из оригинала 26. 04. 2007. г. Приступљено 21. 11. 2015.
- Wilf, Herbert S. (1989). „Chapters 1–3”. Combinatorial algorithms: an update. SIAM. ISBN 978-0-89871-231-5.
Спољашње везе[уреди | уреди извор]
- "Gray Code" demonstration by Michael Schreiber, Wolfram Demonstrations Project (са Метематичком имплементацијом). 2007.
- NIST Dictionary of Algorithms and Data Structures: Gray code
- Hitch Hiker's Guide to Evolutionary Computation, Q21: What are Gray codes, and why are they used?, укључујући C код за претварање између бинарних и BRGC
- Subsets or Combinations Може да генерише BRGC низ
- "The Structure of Single-Track Gray Codes" Архивирано на сајту Wayback Machine (10. март 2007) by Moshe Schwartz, Tuvi Etzion
- Single-Track Circuit Codes Архивирано на сајту Wayback Machine (7. јун 2011) by Hiltgen, Alain P.; Paterson, Kenneth G.
- Dragos A. Harabor користи „Gray codes in a 3D digitizer”. Архивирано из оригинала 22. 11. 2015. г. Приступљено 21. 11. 2015..
- појединачна трака Грејевог кода, бинарно chain codes (Lancaster 1994), и linear feedback shift registers сви су корисни у проналажењу нечије апсолутне позиције на појединачној траци ротационог енкодера ( или неког другог сензора положаја ) .
- Computing Binary Combinatorial Gray Codes Via Exhaustive Search With SAT Solvers by Zinovik, I.; Kroening, D.; Chebiryak, Y.
- AMS Column: Gray codes
- Optical Encoder Wheel Generator
- ProtoTalk.net – Understanding Quadrature Encoding – Омоти куадратуре кодирање детаљнији са фокусом на роботским апликацијама

















































