Метода потенцијала чворова

Први Кирхофов закон је основа методе потенцијала чворова.

У анализи електричних кола, метода потенцијала чворова је метода за одређивање напона (потенцијалне разлике) између чворова (тачака где се везују гране кола или елементи) у електричном колу у односу на струје грана у колу.

У анализи електричних кола користећи Кирхофове законе, може се користити метода потенцијала чворова користећи Први Кирхофов закон или метода контурних струја која користи други Кирхофов закон. Метода потенцијала чворова даје једначину за сваки чвор захтевајући да збир струја грана ка том чвору буде једнак 0. Струје грана кола су записане у односу на напоне чворова. Као последица, свака релација везана за грану кола мора да има једначину која је функција напона. На пример, за отпорник, I_branch = V_branch * G, где је G (=1/R) адмитанса (кондуктанса) отпорника.

Методу потенцијала чворова је могуће користити када све гране елемената у електричном колу имају адмитансу коју је могуће одредити. Метода потенцијала чворова производи мали број једначина за електрично коло, које могу бити решене ручно уколико је електрично коло мало, или брзо решене користећи линеарну алгебру и компјутер. Због малог броја једначина, многи програми за симулацију електричних кола (СПАЈС) користе методу потенцијала чворова за решавање кола. Када елементи немају адмитансу коју је могуће одредити, уопштенији облик методе потенцијала чворова (модификована метода потенцијала чворова) може да се искористи за решавање.

Иако се многи једноставни примери методе потенцијала чворова фокусирају на линеарне елементе, комплексније нелинеарне мреже такође могу да се реше користећи Њутнову методу како би претвориле нелинеарни проблем у скуп линеарних проблема.

Начин рада

1. Уочити све повезане проводнике у електричном колу. Они чине чворове који се користе у методи потенцијала чворова.
2. Одредити један чвор који ће представљати нулти потенцијал. Одабир овог чвора не утиче на резултат и битан је само због конвенције. Одабирање чвора са највише проводника који су на њега повезани за нулти чвор може да упрости анализу кола.
3. Доделити променљиву за сваки чвор кола чији потенцијал није познат. Ако је потенцијал неког чвора познат, није потребно додељивати му променљиву.
4. За сваки непознати напон, формирати формулу на основу првог Кирхофовог закона. Простије речено, сабрати све струје које се крећу од чвора и ка њему и њихову суму изједначити са 0. Налажење струја између два чвора није ништа теже од "чвор на коме сте тренутно, минус чвор ка коме се крећете, подељено са отпором између два чвора."
5. Ако постоје напонски извори између два непозната напона, повезати два чвора тако да чине суперчвор. Струје два чвора се комбинују у једну једначину, и формира се нова једначина за напоне.
6. Решити систем добијених једначина за сваки непознати напон.

Примери

Једноставан случај

Једноставан пример електричног кола за један непознат напон, V₁.

Једини непознат напон у овом колу је V₁. Постоје три гране ка овом чвору и самим тим три струје које треба размотрити. Позитиван смер струја у једначинама је онај који се поклапа са смером од чвора.

1. Струја кроз отпорник R₁: (V₁ - V_S) / R₁
2. Струја кроз отпорник R₂: V₁ / R₂
3. Струја кроз струјни извор I_S: -I_S

Помоћу првог Кирхофовог закона добијамо:

${\frac {V_{1}-V_{S}}{R_{1}}}+{\frac {V_{1}}{R_{2}}}-I_{S}=0$

Ова једначина може да се реши у односу на V₁:

$V_{1}={\frac {\left({\frac {V_{S}}{R1}}+I_{S}\right)}{\left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)}}$

На крају, непознат напон може да се реши уметањем нумеричких вредности уместо променљивих у формулама. Било коју непознату струју је лако израчунати када су познати сви напони у електричном колу.

$V_{1}={\frac {\left({\frac {5{\text{ V}}}{100\,\Omega }}+20{\text{ mA}}\right)}{\left({\frac {1}{100\,\Omega }}+{\frac {1}{200\,\Omega }}\right)}}\approx 4.667{\text{ V}}$

Суперчворови

У овом колу, V_A је између два непозната напона, и самим тим је суперчвор.

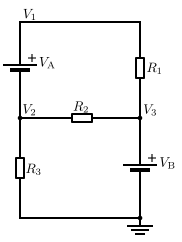
У овом колу на почетку имамо два непозната напона V₁ и V₂. Напон V₃ је већ познат као V_B јер је други крај напонског извора на потенцијалу 0.

Струја која постоји кроз напонски извор V_A не може да се израчуна директно. Зато не можемо да напишемо једначине за V₁ или V₂. Али, знамо да иста струја која напушта чвор V₂ мора да уђе у чвор V₁. Иако чворови не могу да се реше засебно, знамо да је комбинована струја ова два чвора једнака 0. Ово сједињавање два чвора се назива техника суперчвора, и тражи једну додатну једначину: V₁ = V₂ + V_A.

Комплетан скуп једначина за ово коло је:

${\begin{cases}{\frac {V_{1}-V_{\text{B}}}{R_{1}}}+{\frac {V_{2}-V_{\text{B}}}{R_{2}}}+{\frac {V_{2}}{R_{3}}}=0\\V_{1}=V_{2}+V_{\text{A}}\\\end{cases}}$

Заменом V₁ у прву једначину и решавањем у односу на V2, добијамо:

$V_{2}={\frac {(R_{1}+R_{2})R_{3}V_{\text{B}}-R_{2}R_{3}V_{\text{A}}}{(R_{1}+R_{2})R_{3}+R_{1}R_{2}}}$

Литература

• Paul Dimo (1975). Nodal Analysis of Power Systems. Kent: Abacus Press. 

Спољашње везе

• Branch current method
• Online four-node problem solver
• Simple Nodal Analysis Example