Проблем уметничке галерије

Пример галерије коју оптимално покривају 3 стражара.

Проблем уметничке галерије или проблем музеја је проблем видљивости у рачунарској геометрији. Потиче из проблема чувања уметничке галерије са минималним бројем стражара који без промене положаја могу да надгледају читаву галерију. У рачунарској геометрији се просторије уметничке галерије представљају као прост полигон, а сваки стражар је представљен тачком у полигону. Каже се да скуп тачака $S$ чува полигон ако за сваку тачку $p$ у полигону постоји неко $q\in S$ тако да дуж између $p$ и $q$ лежи у унутрашњости полигона.

Примене проблема уметничке галерије

Проблем уметничке галерије припада пресеку роботике, оптимизације и рачунарске графике, а видљивост се садржи у свим овим пољима. Постоје бројне практичне примене као што су постављање камера у излозима, распоред извора светлости у соби или постављање радарских станица у планинским пределима.

Разноликости у облицима полигона су велика и глобално решење које би било довољно за све типове полигона још није пронађено. Ипак, у специјалним случајевима, понуђена су разноврсна решења проблема уметничке галерије за одређене типове полигона.

У две димензије

Триангулација полигона.

Оригинални проблем има бројне варијације које такође носе исти назив. У неким верзијама су стражари ограничени на периметар или чак на темена полигона, док друге верзије захтевају да само периметар или неки његов подскуп буде под надзором.

Решавање верзије у којој стражари морају да се поставе у темена, и само темена треба да се чувају, еквивалентно је решавању проблема доминантног скупа на графу видљивости полигона.

Хваталова теорема уметничке галерије

Хваталова теорема уметничке галерије, названа по Ватславу Хваталу(Václav Chvátal), даје горњу границу за минималан број стражара. Тврди се да је $\left\lfloor n/3\right\rfloor$ стражара увек довољно, а некада и неопходно, да чува прост полигон са $n$ темена.

Виктор Кли је 1973. године први поставио питање о броју потребних темена или стражара, а Хватал га је убрзо доказао. Хваталов доказ је касније упростио Стив Фиск преко аргумента 3-обојивости.

Фисков кратак доказ

3-бојење чворова триангулисаног полигона. Чувари су на пример плаве тачке.

Фиск 1978. године доказује теорему уметничке галерије на следећи начин: Прво се полигон $S$ триангулише без додавања нових темена. Свака таква триангулација има бојење са три боје $a,b,c$. Нека је $T_{k}$ скуп темена боје $a$, и претпостављамо да $|T_{a}|\leq |T_{b}|\leq |T_{c}|$. Ако кажемо да је $T=T_{k}$ из тога следи $|T|\leq n/3$. Коначно, свака тачка $q\in S$ се налази у неком троуглу од $S$, и сваки троугао од $S$ има тачку $p\in T$ на њему. Пошто су троуглови конвексни, имамо да $pq\subset S$.

Пошто три боје деле $n$ темена полигона, боја са најмање темена чини исправан скуп стражара са највише $\left\lfloor n/3\right\rfloor$ стражара.

Генерализације

Хваталова горња граница остаје исправна и ако променимо проблем тако да стражаре, уместо само у теменима, поставимо у било коју тачку која припада полигону.

Постоји велики број других генерализација и специјализација оригиналног проблема уметничке галерије које модел чине реалистичнијим и интересантнијим. Промене се деле на две врсте: можемо мењати дозвољене облике које може имати галерија или можемо мењати способности и сврху стражара.

Мењање облика галерије

• 
  Конвексан полигон
• 
  Ортогонални полигон
• 
  Галерија са рупом

Најједноставнији полигон за овај проблем, је конвексан полигон, пошто је у том случају потребан само један стражар који се може налазити на било којој тачки која припада полигону.

За ортогоналне полигоне, чије ивице (зидови) међусобно заклапају угао од 90 степени, је потребно само $\lfloor n/4\rfloor$ чувара. За ову теорему постоје бар три различита доказа, од којих ниједан није једноставан.

Галерије са рупама. Правимо модел галерије тако што допуштамо да се у унутрашњости галерије поставе полигони (рупе). Чувари се не смеју постављати у унутрашњости рупа. Поставља се основно питање минималног броја чувара за галерију са $w$ зидова и $h$ рупа, где се зидови рупа такође рачунају као зидови галерије. Теорема даје горњу границу за минималан број стражара у оваквом моделу галерије и она иѕноси $\lfloor (w+h)/3\rfloor$.

Мењање способности стражара

Тврђава, чију околину чувају стражари.

У сличном проблему се тражи минималан број стражара који могу прекрити спољашњост полигона (“Проблем тврђаве”). За овај проблем је $\lfloor n/2\rfloor$ стражара понекада потребно, а увек довољно, што значи да је бесконачну спољашњост теже прекрити од коначне унутрашњости. У проблему затворског дворишта, чувари могу бити постављени на ивицама полигона, и тражи се да свака тачка у равни, како унутар полигона тако и изван њега, буде под стражом. У суштини овај проблем представља спој проблема уметничке галерије за унутрашњост полигона и проблема тврђаве за његову спољашњост.

Рачунарска сложеност

У верзијама проблема одлучивања проблема уметничке галерије, као улаз су дати полигон и број $k$, и мора се израчунати да ли дати полигон може бити прекривен са $k$ или мање чувара. Овај проблем и све његове стандардне варијације (као што је на пример ограничавање положаја чувара на само темена или странице) су НП-тешке. Што се тиче апроксимационих алгоритама за одређивање минималног броја чувара, Еиденбенц, Штам, и Видејер су 2001. године доказали да је проблем апроксимационо тежак, што значи да је мало вероватно да се помоћу апроксимационог алгоритма полиномијалне сложености може пронаћи апроксимациони однос бољи од неке константе. Међутим, константан апроксимациони однос није откривен. Уместо тога може се остварити логаритамска апроксимација за минимални број стражара на теменима, и то сводећи проблем на проблем прекривања скупа. Као сто је Валтр показао 1998. године, скуп добијен из проблема уметничке галерије има граничне ВЦ димензије и тиме омогућава коришћење проблема прекривања скупа заснованих на ε-мрежама чији апроксимациони однос представља логаритам оптималног броја стражара, уместо броја темена полигона. За неограничен број стражара се показује да потенцијално бесконачан број позиција додатно компликује проблем.

Међутим, постоје ефикасни алгоритми за налажење скупа са највише $\lfloor n/3\rfloor$ темених стражара, што се слаже са Хваталовом горњом границом. Дејвид Авис и Годфрид Тусеинт су 1981. године доказали да се положај ових чувара може израчунати у $O(nlogn)$ сложености, у најгорем случају, користећи подели па владај алгоритам. Кушеш и Морет су 1992. године направили алгоритам линеарне сложености користећи Фисков кратак доказ и Бернанд Шазелеов линеаран алгоритам за триангулацију временске равни.

Коуто, де Резенде и де Суза су 2011. године предложили алгоритам за темене стражаре. Аутори су извршили опсежне експерименте са неколико класа полигона и показали су да оптимална решења могу бити пронађена за релативно кратко време извршавања, чак и за примере са више од хиљаду темена. Улазни подаци, као и оптимална решења за ове примере, доступни су на интернету.

Уопштење у три димензије

Пример полиедра са унутрашњим тачкама које се не могу видети са било ког темена.

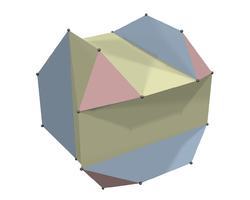
Ако је галерија представљена у три димензије као полиедар, онда стављање једног стражара на свако теме не би гарантовало да ће цела галерија бити под надзором. Иако би све површине полиедра биле под надзором, код неких полиедра постоје тачке у унутрашњости које можда нису под надзором.

Литература

• Aggarwal, A. (1984), The art gallery theorem: Its variations, applications, and algorithmic aspects, Ph.D. thesis, Johns Hopkins University .
• Avis, D.; Toussaint, G. T. (1981), „An efficient algorithm for decomposing a polygon into star-shaped polygons” (PDF), Pattern Recognition, 13 (6): 395—398, doi:10.1016/0031-3203(81)90002-9 .
• Chvátal, V. (1975), „A combinatorial theorem in plane geometry”, Journal of Combinatorial Theory, Series B, 18: 39—41, doi:10.1016/0095-8956(75)90061-1 .
• Couto, M.; de Rezende, P.; de Souza, C. (2011), Benchmark instances for the art gallery problem with vertex guards .
• Eidenbenz, S.; Stamm, C.; Widmayer, P. (2001), „Inapproximability results for guarding polygons and terrains” (PDF), Algorithmica, 31 (1): 79—113, doi:10.1007/s00453-001-0040-8, Архивирано из оригинала (PDF) 24. 06. 2003. г., Приступљено 28. 01. 2016 .
• Fisk, S. (1978), „A short proof of Chvátal's watchman theorem”, Journal of Combinatorial Theory, Series B, 24 (3): 374, doi:10.1016/0095-8956(78)90059-X .
• Ghosh, S. K. (1987), „Approximation algorithms for art gallery problems”, Proc. Canadian Information Processing Society Congress, стр. 429—434 .
• Lee, D. T.; Lin, A. K. (1986), „Computational complexity of art gallery problems”, IEEE Transactions on Information Theory, 32 (2): 276—282, doi:10.1109/TIT.1986.1057165 .
• Lubiw, A. (1985), „Decomposing polygonal regions into convex quadrilaterals”, Proc. 1st ACM Symposium on Computational Geometry, стр. 97—106, ISBN 978-0-89791-163-4, doi:10.1145/323233.323247 .
• O'Rourke, Joseph (1987), Art Gallery Theorems and Algorithms, Oxford University Press, ISBN 978-0-19-503965-8 .

Спољашње везе

• Како чувати уметничку галерију, и још неки проблеми
• Алгоритми и теореме уметничке галерије