Algoritam množenja

Algoritam množenja je algoritam (ili metoda) za množenje dva broja. U zavisnosti od veličine brojeva, mogu se koristiti različiti algoritmi. Efikasni algoritmi množenja postoje još od pojave decimalnog sistema.

Metod mreže (grid metod)

Metod mreže ili metod kutije je uvodni metod za množenje višecifrenih brojeva, i često se uči u osnovnoj školi. To je standardni deo nacionalnog plana i programa za matematiku u osnovnim školama u Engleskoj i Velsu od kasnih 1990-ih godina. Oba faktora (broja) su podeljena na stotine, desetice i jedinice, i proizvodi delova se zatim računaju eksplicitno u relativno jednostavnoj fazi množenja, pre nego što se na kraju saberu da bi se dobio konačni rezultat.

Primer je množenje 34x13, može se izračunati korišćenjem mreže:

  300
   40
   90
 + 12
 ————
  442

×	30	4
10	300	40
3	90	12

a zatim se sabiraju da bi se dobilo 442, bilo u jednoj sumi, ili kroz formiranje red po red zbirova (300 + 40) + (90 + 12) = 340 + 102 = 442.

Ovaj pristup računanja (mada ne obavezno sa eksplicitnim aranžmanom mreže) je takođe poznat i kao algoritam delimičnih proizvoda. Njegova suština je odvojeno računanje jednostavnih množenja, pri čemu se sabiranje ostavlja za krajnju fazu.

Metod mreže se u principu može primeniti na faktore bilo kojih veličina, iako broj potproizvoda može postati jako veliki kako se povećava broj cifara. Svakako predstavlja korisni eksplicitni metod kao uvod za ideju množenja višecifrenih brojeva; i u doba kada se većina računanja vrši pomoću digitrona, ovo može biti jedini algoritam množenja koji će učenicima ikad biti potreban.

Dugo množenje

Ako se koristi pozicioni sistem brojeva, prirodan način množenja koji se uči u školama je metod dugog množenja, nekad nazivan i standardnim algoritmom: pomnožiti množenik svakom cifrom množioca i onda ih sabrati sve ispravno. Ovaj način zahteva memorisanje tablice množenja za jednocifrene brojeve.

Ovo je uobičajeni algoritam za množenje većih brojeva na papiru, čija je osnova 10. Kompjuteri su na početku koristili sličan algoritam pomeranja i dodavanja brojeva čija je osnova 2, ali moderni procesori imaju optimizovana kola za brza množenja koristeći efikasnije algoritme, po ceni složenije hardverske realizacije. Osoba koja radi dugo množenje na papiru će zapisati sve proizvode i zatim ih sabrati, ali osoba koja koristi abakus će sabirati proizvode nakon svakog računanja.

Primer

Ovaj primer koristi dugo množenje da bi se pomnožio 23 958 233 (množenik) sa 5830 (množilac), i dobija se 139 676 498 390 (rezultat).

      23958233
 ×         5830
 ———————————————
       00000000 ( =      23,958,233 ×     0)
      71874699  ( =      23,958,233 ×    30)
    191665864   ( =      23,958,233 ×   800)
 + 119791165    ( =      23,958,233 × 5,000)
 ———————————————
   139676498390 ( = 139,676,498,390        )

Ispod se nalazi pseudokod koji opisuje proces množenja naveden iznad. U njoj se nalazi samo jedan red koji održava sumu koja će na kraju biti finalni rezultat. Obratiti pažnju da se operator += koristi da označi sumu postojeće vrednosti i sačuva operaciju, kao u programskim jezicima C i Java.

multiply(a[1..p], b[1..q], base) // Operandi na desnoj poziciji sadrže cifru 1
  product = [1..p+q]                                        //Dodeliti prostor za rezultat
  for b_i = 1 to q                                          // za sve cifre u b
    carry = 0
    for a_i = 1 to p                                        //za sve cifre u a
      product[a_i + b_i - 1] += carry + a[ai] * b[bi]
      carry = product[ai + bi - 1] / base
      product[a_i + b_i - 1] = product[ai + bi - 1] mod base
    product[b_i + p] += carry                               // poslednja cifra dolazi  iz konačnog prenosa
  return product

Množenje rešetkom

Množenje rešetkom ili sitom je algoritamski ekvivalent dugog množenja. Zahteva pipremu rešetke, tj mreže nacrtane na papiru koja vodi računanje i razdvaja množenja od sabiranja. Prvi put je korišćen u Evropi 1202. godine u Fibonačijevoj "Liber Abaci". Leonardo opisuje ovu operaciju kao mentalnu, koristeći i desnu i levu ruku kako bi prenosio prelazna računanja. Matrakci Nasuh je predstavio 6 različitih varijanti ove metode u knjizi iz 16.veka "Umdet-ul Hisab". Korišćena je u Enderun školama širom Otomanskog carstva. Napijerove šipke ili kosti su takođe koristile ove metode.

Kao što je prikazano u primeru, množenik i množilac su napisani iznad i desno od rešetke ili sita. Tokom faze množenja, rešetka se popunjava dvocifrenim proizvodima odgovarajućih cifara koje označavaju svaki red i kolonu. Desetice idu u gornji levi ugao.

Tokom faze sabiranja, rešetka se sabira na dijagonalama. Na kraju, ako je neophodna faza pomeranja, rešenje prikazano na levim i donjim stranama rešetke se konvertuje u normalnu formu prenosom cifara desetica kao u algoritmu dugog množenja.

Primer

Prvo, postaviti mrežu tako da se prvo obeleže redovi i kolone sa brojevima koji će biti pomnoženi. Onda popuniti kutije sa deseticama u gornjim trouglovima i jedinicama u donjim.

Na kraju, sabrati brojeve duž dijagonala i preneti koliko treba da bi se dobio rezultat.

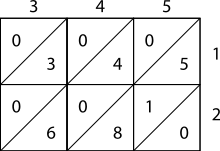
Slika na desnoj strani pokazuje kako izračunati 345 × 12 koristeći množenje rešetkom. Kao složeniji primer možemo razmotriti sliku ispod koja prikazuje množenje 23 958 233 sa 5830, rezultat je 139 676 498 390. Obratiti pažnju da je 23 958 233 na vrhu rešetke a 5830 je sa desne strane. Proizvodi popunjavaju rešetku ili sume tih proizvoda (na dijagonali) su duž levih i donjih strana. Zatim su te sume izračunate, kao što je prikazano.

2 3 9 5 8 2 3 3 +---+---+---+---+---+---+---+---+- |1 /|1 /|4 /|2 /|4 /|1 /|1 /|1 /| | / | / | / | / | / | / | / | / | 5 01|/ 0|/ 5|/ 5|/ 5|/ 0|/ 0|/ 5|/ 5| +---+---+---+---+---+---+---+---+- |1 /|2 /|7 /|4 /|6 /|1 /|2 /|2 /| | / | / | / | / | / | / | / | / | 8 02|/ 6|/ 4|/ 2|/ 0|/ 4|/ 6|/ 4|/ 4| +---+---+---+---+---+---+---+---+- |0 /|0 /|2 /|1 /|2 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 3 17|/ 6|/ 9|/ 7|/ 5|/ 4|/ 6|/ 9|/ 9| +---+---+---+---+---+---+---+---+- |0 /|0 /|0 /|0 /|0 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 0 24|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0| +---+---+---+---+---+---+---+---+- 26 15 13 18 17 13 09 00	01 002 0017 00024 000026 0000015 00000013 000000018 0000000017 00000000013 000000000009 0000000000000 ————————————— 139676498390
		= 139,676,498,390

Binarno množenje

Za brojeve čija je osnova 2, dugo množenje se svodi na trivijalnu operaciju. Za svaki bit jedinicu u multiplier, pomeriti multiplicand za odgovarajući iznos, a zatim sabrati pomerene vrednosti. U zavisnosti od arhitekture procesora računara i izbora multipliera, moze biti brže kodirati ovaj algoritam koiristeći hardversko pomeranje i sabiranje bitova nego zavisiti od instrukcija za množenje, kada je multiplier fiksiran i broj sabiranja je mali.

Ovaj algoritam se naziva još i seljačko množenje, jer je bio u širokoj upotrebi među onima koji nisu bili školovani i samim tim nisu upamtili tablicu množenja koje zahteva dugo množenje. Ovaj algoritam se takođe koristio i u drevnom Egiptu.

Na papiru, zapišite u jednoj koloni brojeve koje dobijete kada više puta prepolovite multiplier, ignorišući ostatak. u koloni pored njega u više navrata udvostručiti multiplicand. Precrtati svaki red u kome je poslednja cifra prvog broja parna, i dodajte preostale brojeve u drugu kolonu kako bi se dobio rezultat.

Glavne prednosti ove metode su te da može da se nauči brzo, memorisanje nije potrebno, i može se izvesti korišćenjem tokena kao sto su čipovi za poker ako papir i olovka nisu dostupni. Međutim, ima više koraka od dugog množenja tako da može da bude nezgrapno kada su u pitanju veliki brojevi.

Primeri

Ovaj primer koristi binarno množenje da pomnoži 11 sa 3, pri čemu se dobija rezultat 33.

Decimalno:     Binarno:
11   3       1011  11
5    6       101  110
2   12       10  1100
1   24       1  11000
    ——         ——————
    33         100001

Eksplicitni opis koraka: 11 i 3 su napisani na vrhu. 11 je prepolovljeno na 5.5 a 3 je udvostručeno na 6. Frakcioni deo, tj. deo iza decimale se odbacuje. 5 je prepolovljeno na 2.5 a 6 je duplirano na 12. Decimalni deo se odbacuje.

Broj u levoj koloni je paran, tako da se deo u desnoj koloni odbacuje. 2 se polovi a 12 se duplira.

Sve neprecrtane vrednosti se saberu: 3+6+24=33.

Ovaj metod radi jer je množenje distributivna operacija, tako da

${\begin{aligned}3\times 11&=3\times (1\times 2^{0}+1\times 2^{1}+0\times 2^{2}+1\times 2^{3})\\&=3\times (1+2+8)\\&=3+6+24\\&=33.\end{aligned}}$

Komplikovaniji primer, sa korišćenjem prethodno navedenih cifara (23 958 233 i 5 830):

Decimal:             Binary:
5830  23958233       1011011000110  1011011011001001011011001
2915  47916466       101101100011  10110110110010010110110010
1457  95832932       10110110001  101101101100100101101100100
728  191665864       1011011000  1011011011001001011011001000
364  383331728       101101100  10110110110010010110110010000
182  766663456       10110110  101101101100100101101100100000
91  1533326912       1011011  1011011011001001011011001000000
45  3066653824       101101  10110110110010010110110010000000
22  6133307648       10110  101101101100100101101100100000000
11 12266615296       1011  1011011011001001011011001000000000
5  24533230592       101  10110110110010010110110010000000000
2  49066461184       10  101101101100100101101100100000000000
1  98132922368       1  1011011011001001011011001000000000000
  ————————————          1022143253354344244353353243222210110 (before carry)
  139676498390         10000010000101010111100011100111010110

Ostali algoritmi množenja

• Pomeranje i sabiranje
• Množenje "quarter square"
• Algoritam za množenje brojeva blizu celog broja
• Gausov kompleksni algoritam množenja
• Karacubin algoritam množenja
• Toom-Cook algoritam množenja
• Furijeove transformacije

Vidi još

• Binarni množenik
• Algoritam deljenja
• Logaritam
• Logaritmar

Spoljašnje veze

1. "BBC - back to school for parents"
2. "BBC - Why parents can't do math today" Архивирано на сајту Wayback Machine (4. март 2016)
3. Novel Methods of Integer Multiplication and Division
4. Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers
5. Fast Fourier transformations: a tutorial review and a state of the art
6. Faster integer multiplications