Универзални закон гравитације

Математичар и физичар Исак Њутн у периоду од 1665. до 1685, развио је своју теорију механике, засновану на убрзању, а не само на проучавању брзине, како су то чинили Галилеј и Декарт пре њега. Кључна чињеница коју је Њутн први запазио је да је сила која делује на јабуку која пада са дрвета заправо иста сила која делује на Земљу да се окреће око Сунца. Из тог сазнања потекао је Њутнов закон гравитације, тј. универзални закон гравитације, који се убраја у четврти Њутнов закон, поред 3 основна закона класичне механике.[1] Универзални закон гравитације је формулисан у Њутновом делу Philosophiæ Naturalis Principia Mathematica, које је прву пут било објављено 5. јула 1687. Кад је Њутн представио Књигу 1 необјављеног текста у априлу 1686. Краљевском друштву, Роберт Хук је тврдио да је Њутн добио закон инверзног квадрата од њега.
У данашњем језику, закон наводи да свака тачка масе привлачи сваку другу тачку масе са силом која делује дуж линије која спаја тачке. Сила је пропорционална производу две масе, и инверзно пропорционална квадрату растојања између њих.[2]
Формулација закона[уреди | уреди извор]
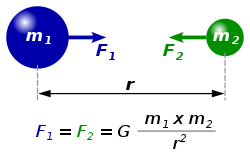
- Гравитациона сила којом се привлаче тела 1 и 2 сразмерна је производу њихових маса и , а обрнуто> сразмерна квадрату њиховог растојања, .
, је гравитациона константа која износи (или ), а је јединични вектор усмерен од тела 1 према телу 2. Негативни предзнак означава да је сила међу телима привлачна сила.
Доказ[уреди | уреди извор]
Други Њутнов закон:
Основни закон динамике, тј. Други Њутнов закон, који полази од Декартовог принципа инерције (одржање количине кретања), показује да збирно деловање сила на тела једнако , где је инертна маса (која отежава кретање тела), и где је убрзање (ритам промене брзине).
Уобичајеним називима речено:
Величина силе на неко тело директно је сразмерна убрзању и маси тог тела.
где је F сила, m маса, a убрзање.
Кеплерови закони и Закон о центрифугалној сили:
С друге стране, из Кеплерових закона, који су изведени из посматрања кретање тела у Сунчевом систему, и закона Кристијана Хајгенса о центрифугалној сили, Њутн је закључио да гравитациона сила између два тела делује по правој линији између њих и обрнуто је пропорционална квадрату њиховог растојања, тј. сразмерна је са , где је растојање између тела.
Гравитациона константа
Сматрајући да је сила гравитације пропорционална количини материје присутној у телу која делују овом силом (двоструко веће тело делује двоструко већом силом), пертпоставио је да је сила пропорционална величини коју је назвао гравитациона маса, пропорционална количини материје у телу и његовој способности да врши привлачно деловање.
Трећи Њутнов закон:
По принципу акције и реакције, сила којом друго тело делује на прво је једнака (и усмерена у супротном смеру) сили којом прво тело делује на друго. Ова сила је пропорционална , гравитационој маси другог тела.
Закључак:
Њутн је желео да обједини законе који важе на Земљи са онима који важе на небу (астрономија), нарочито оне који се односе на Земљину тежу и кретање планета).
Основни закон динамике се стога може записати као: . Ако је убрзање (и брзина) тела које је у слободном паду независно од инерционе масе (као што је показао Галилејев експеримент), онда за тело важи , дакле гравитациона маса је једнака инерционој маси, што не зависи од врсте и састава тела. Њутн је тестирао ову теорију на много примера и није јој нашао изузетак.
Ако занемаримо остале утицаје и претпоставимо да сила делује тренутно, без кашњења, гравитациону сила између два тачкаста тела може се објаснити на следећи начин:
- , где је константа под именом гравитациона константа.
Одавде добијамо и коначни запис Универзалног закона гравитације у скаларном облику:
И у векторском облику:
Пример[уреди | уреди извор]

Наћи привлачну силу гравитације између планете Земље и Сунца и њен интензитет.
Познате вредности су:
- гравитациона константа:
- удаљеност Земље од Сунца
- маса Сунца
- маса Земље
Универзални закон гравитације гласи:
где је јединични вектор од тела 1 ка телу 2.
На основу горенаведеног, добијамо да је тражена сила:
а њен интензитет:
Знак минус (-) у једначини силе показује да је сила између Земље и Сунца привлачна сила.
Општост Универзалног закона гравитације[уреди | уреди извор]

(1) Путање планета су елипсе, са жариштима ƒ1 и ƒ2 за прву планету и ƒ1 и ƒ3 за другу планету. Сунце је смештено у жаришту ƒ1.
(2) Два засенчена подручја A1 и A2 имају једнаке површине и време за планету 1 да прекрије подручје A1 је једнако да прекрије подручје A2.
(3) Укупна опходна времена планета 1 и планета 2 имају однос t13/2 : t23/2.
Колико је Њутнов закон гравитације општији у односу на законе који су до тада постојали и који су били и експериментално потврђени, показује чињеница да се сви ти закони могу доказати из њега и да они представљају само неке од специјалних случајева тог закона.
Кеплерови закони[уреди | уреди извор]
Помоћу Универзалног закона гравитације, могу се доказати и сви Кеплерови закони и уочавају се грешке у Трећем Кеплеровом закону.
Галилејев закон[уреди | уреди извор]
Њутнов закон гравитације може да искаже Галилејев закон. Ако се са означи полупречник земље, а је маса Земље, добија се да је m·s−2.
Примена[уреди | уреди извор]

Као и свака теорија, и Универзални закон гравитације је од хипотезе експериментално потврђен.
Једно од открића, којем је основну подлогу дао управо Универзални закон гравитације, је откриће да је могуће у ваздух подигнути, тј. послати на небо и предмете који су тежи од ваздуха.
Закон гравитације и кретања тела[уреди | уреди извор]




Појаве у природи тумаче се међуделовањима (интеракцијама). Њутнов закон гравитације је математички опис гравитационе силе или гравитационе интеракције - силе којом се узајамно привлаче две масе. Док су Кеплерови закони описивали начин кретања планета, Њутнов закон гравитације је помогао да се растумачи зашто се планете крећу баш тако како се крећу. Њутн је закон извео на темељу практичног искуства и теоријских разматрања тадашње физике и астрономије, укључивши Кеплерове законе. Обратно, математичким се путем из Њутновог закона гравитације могу извести Кеплерови закони. Али не само то. У природи има кретања која су много сложенија од кретањаа поједине планете око Сунца. Већ је кретање планетоида и комета сложеније од кретања планета. Исто је тако сложеније кретање мноштва звезда у једном скупу звезда, или звезда једне галаксије, а сва су она условљена Њутновом силом. Стога је Њутнов закон гравитације много општији и и важи у целом свемиру.
Својства те гравитационе силе су следећа. Она је узајамна, привлачна и централна сила. Узајамна је зато што једнаком силом којом тело масе M привлачи масу m, привлачи и тело масе m масу M. Централна је зато што је усмерена од једне масе према другој. Надаље, сила је сразмерна маси сваког тела посебно, а њена величина опада обрнуто сразмерно с квадратом удаљености. Ако се размак тела удвостручи, сила се смањи четири пута; ако се утростручи, смањи се девет пута.
Константа G (универзална гравитациона константа) је константа пропорционалности и према мерењима износи око 6,67428 ∙ 10−11 N m² kg−2. Тела обично се представљају малим куглама. Закон треба примењивати на тачкаста тела (тела сажета у материјалне тачке). Ако тела нису тачкаста, већ проширена, тада је укупна сила између њих једнака збиру свих сила између сваке две материјалне тачке. Стога гравитационо поље око стварног (реалног) тела може бити веома сложено.[3]
Слободни пад[уреди | уреди извор]
Гравитациона сила је узрок кретања и промјена стања кретања. У пољу гравитације тела се крећу убрзано. Зато се у убрзању тела одражавају својства гравитационе силе. Убрзање или акцелерација неког малог тела масе m које се налази у пољу сферног тела масе M, према Другом Њутновом закону кретања или темељном закону кретања гласи:
Константа пропорционалности између силе и убрзања је маса убрзаваног тела. На тело масе m делује Њутнова сила, јер се оно налази у гравитационом пољу које окружује масу M. Изједначавањем горњих израза добија се:
То је убрзање (акцелерација) тела масе m у гравитационом пољу масе M, на растојању r од масе M. Убрзање или акцелерација има уједно димензију јачине гравитационог поља; јачина гравитационог поља је однос гравитационе силе и убрзаване масе. Уобичајено је да се слободни пад (или кретање косином) узима као пример униформног убрзаног кретања (кретања са сталним убрзањем). Притом се претпоставља да нема отпора ваздуха или трења. Горњи математички израз треба узимати с опрезом. Ако и нема отпора, тело ће се кретати сталним убрзањем само на веома малом делу пута, на оном делу на којему се r врло мало мења. Према томе, слободни пад се може узимати као пример униформног убрзаног кретања једино код малих висина пада. Ако је убрзање стално, пут s преваљен у смеру убрзања за време t једнак је:
Кружење сателита[уреди | уреди извор]
Исак Њутн је схватио да је кружно кретање састављено од две компоненте, од кретања сталном брзином по правцу и од униформно убрзаног кретања са смером према средишту кружења. Кад не би било привлачења, тело би униформном брзином vk одмицало по правцу и за време t прешло пут vk∙t. Исто тако, због гравитационог привлачења, тело пада према центру и у том паду, у време t, превали пут gt2/2. Ако тело ипак остаје на кружници, мора бити да се оно током времена t за толико одмакне од кружнице за колико уједно и падне на кружницу. Тај процес присутан је на сваком месту кружнице, на сваком ма како малом одсечку пута. Ако би брзина кретања v била мања од брзине кружења vk, то тело би због слободног пада пришло центру Земље више него што би се у једноликом кретању по правцу од ње одмакнуло, па би тако прелазило с кружнице већег полупречника на кружницу мањег полупречника, те би у спирали напокон пало на Земљу.
Присили ли се неко тело да се на вртешци креће брзином v, тада оно у смеру према центру има убрзање g (центрипетално убрзање). Између брзине кретања v по кружној стази полупречника r и центрипеталне акцелерације g постоји веза:
Креће ли се тело по кружници и појача ли се центрипетална сила, порашће и убрзање и брзина. Ако је сила привлачења гравитациона, и у центру кретања се налази маса M, тада је центрипетално убрзање потпуно одређено и једнако изразу:
Тим условом се за дати полупречник стазе од свих могућих центрипеталних убрзања одабира само једно убрзање (акцелерација), а њој одговара само једна, потпуно одређена брзина. Изједначавањем горња два израза, добија се:
За Земљу (M = 6 ∙1024 kg) брзина кружења или орбитална брзина на самој површини (r = 6 378 km) износила би 7 910 m/s или 7,91 km/s. Та се брзина зове и првом космичком брзином. На сваком другом нивоу изнад површине Земље брзина кружења има другу вредност.[4]
Ослобађање сателита[уреди | уреди извор]
Када се брзина сателита повећа изнад брзине кружења vk долази до издужења стазе (путање). Кружница прелази у елипсу, а елипса малог ексцентрицитета прелази у елипсу већег ексцентрицитета. Када стаза постане парабола, тело ће напустити Земљину близину и слободно одлетјети у међупланетарни простор. То је брзину ослобађања vo или друга космичка брзина. Тела могу бити међусобно везана, или слободна. Тело је везано и чини један физички систем са Земљом када лежи на њој или се креће око ње затвореном путањом. Уопштено, тело има и кинетичку енергију и гравитациону потенцијалну енергију (енергију положаја у гравитационом пољу). Потенцијална енергија Ep масе m у околини масе M једнака је:
Договором је потенцијалној енергији додељен негативан предзнак. На мањој удаљености р потенцијална енергија је негативнија него на већој удаљености. С повећањем размака потенцијална енергија поприма мање негативну вредност, а на бесконачној удаљености износ јој падне на нулу. Заправо, релативно највећу вредност има потенцијална енергија на највећој удаљености; то је смисао негативног предзнака. У строгом значењу тело је слободно када се налази на неизмерној удаљености од Земље. С обзиром на то да Земља није сама у свемиру, већ је свемирско гравитационо поље сложено од многих појединачних, тело ће се увек налазити под њиховим утицајем. Зато је и питање слободе више практичко питање: на великим удаљеностима од Земље тело се налази у слободном стању. Однос гравитационе потенцијалне енергије и масе m, дакле израз - GM/r, зове гравитациони потенцијал.
Може се замислити поступак ослобађања тела у случају када је тело на почетку мировало на Земљи, а на крају мировало на практично бесконачној удаљености од Земље. Како је кинетичка енергија у таквом случају и на почетку и на крају поступка једнака нули, то ће тело морати премостити разлику потенцијалне енергије Ep која постоји између површине Земље и бесконачне удаљености. Промена енергије једнака је коначној вредности мање почетне вредности. Будући да се енергија не може ни створити нити изгубити (закон очувања енергије), треба је преузети из кинетичке енергије Ek, тело треба одаслати са Земље с неком почетном брзином vo:
Тело се мора кренути са брзином ослобађања vo:
Поступак се може одвијати и у супротном смеру. При слободном паду од бесконачности до даљине r разлика потенцијалне енергије прелази у кинетичку, и брзина vo коју тело има зависи од удаљености r од центра привлачења масе M. То значи да би тело у слободном паду пало до неког положаја r с истом оном брзином с којом се с тог положаја у гравитационом пољу мора ослободити. Брзина ослобађања са Земље износи 11,2 km/s и назива се још другом космичком брзином. Ако се жели да се тело које већ кружи око масе M ослободи, требаће му до брзине ослобађања доделити мању енергију него кад је лежало на Земље. Брзину тела треба повећати од vk до vo, заправо кинетичкој енергији треба додати износ G M m / 2 r. Телу треба довести још толико кинетичке енергије колико кинетичке енергије већ има. На такав се начин поступа с свемирским летелицама које се отпремају на планете. Оне се најпре лансирају у путању око Земље, где је безваздушни простор, а онда се у одабраном тренутку поново пале ракетни мотори, ракета постиже брзину ослобађања и усмерава летилицу према циљу.
Кретање вештачких сателита[уреди | уреди извор]
Вештачки сателити се лансирају у путање које имају различите ексцентрицитете. Брзина којом се крећу зависи од положаја на путањи. На већим удаљеностима од Земље брзина кружења vk мања је од 7,9 km/s. На слици је неколико облика путање сателита који пролазе тачком која је на некој висини од површине Земље. Тачка најближа Земљи на тој путањи зове се перигеј, а тачка највеће удаљености апогеј. Путања C је кружница и сателит се креће са сталном брзином, с брзином кружења за ту даљину. Стаза D је елиптична. С приближавањем перигеју сателит постиже највећу брзину, која је већа од брзине кружења на том месту; да је једнака брзини кружења, сателит би се кретао кружницом. Елиптичну путању D има вештачки сателит који се креће брзином већом од брзине кружења, а мањом од брзине ослобађања.
По неким особинама кретање вештачких сателита разликује се од кретања природних сателита. Највећа је разлика у томе што је маса вештачких сателита сасвим занемарива према маси Земље. Осим Земље, на путању сателита утичу и Месец и Сунце. Зато се сателит креће у сложеном гравитационом пољу. Ни сама Земља нема једноставно гравитационо поље какво има тачкаста маса, јер је спљоштена на половима, односно испупчена на екватору, а осим тога, унутар већ сложеног облика, материја није једнолико распоређена. Масе су различито распоређене у подручју мора и копна. Већу густину имају слојеви тла који се налазе испод океана, мању слојеви испод копна. Путања сателита стално се поремећује, непрестано се мењају орбитални елементи сателита, те се та поремећења управо могу искористити да би се оценио облик Земље и распоред маса. Подаци добијени након анализе кретања сателита надопуњују податке добијене непосредним геодетским премерима Земље и гравиметријским мерењима (мерењима убрзања силе теже).
Други узрок који доводи до сталне промене путање Земљиног вештачког сателита је отпор Земљине атмосфере. Атмосфера постоји и на врло великим висинама, макар и ретка, па се њен утицај осети након неког времена. Јасно је да је утицај јачи у нижим деловима путање, док је сателит близу перигеја. Сателит губи енергију, апогеј се приближава Земљи и путање се заобљује. Елипса прелази у кружницу, а читава се путања смањује и приближава Земљи. Сателит тоне све дубље и спирално улази у гушће делове атмосфере где изгара, а каткада покоји његов део доспева и до тла.
Види још[уреди | уреди извор]
- Гравитација
- Њутнови закони - основни закони класичне механике
- Кеплерови закони
- Галилејев закон
- Исак Њутн
Референце[уреди | уреди извор]
- ^ Isaac Newton: "In [experimental] philosophy particular propositions are inferred from the phenomena and afterwards rendered general by induction": "Principia", Book 3, General Scholium, at p.392 in Volume 2 of Andrew Motte's English translation published 1729.
- ^ Proposition 75, Theorem 35: p.956 - I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I.Bernard Cohen. University of California Press 1999. ISBN 978-0-520-08816-0. ISBN 978-0-520-08817-7
- ^ Vladis Vujnović : "Astronomija", Školska knjiga, 1989.
- ^ Kozmička brzina, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2014.









































