Višestruki integral

Integral kao površina između dve krive.

Dvostruki integral kao zapremina ispod površine. Pravougli region na dnu tela je domen integracije, dok je površina grafik funkcije sa dve promenljive koja se integriše.

Višestruki intgral je vrsta određenog integrala za funkcije sa više od jedne realne varijable, na primer $f(x,y)$ ili $f(x,y,z)$.

Uvod

Baš kao što određeni integral pozitivne funkcije sa jednom varijablom predstavlja površinu u području između grafa funkcije i x-ose, dvostruki integral pozitivne funkcije dve varijable predstavlja zapreminu u području između površine definisane funkcije i ravni koja sadrži njihove domene. (Treba imati na umu da se ista zapremina može dobiti preko trostrukog integrala - integral funkcije u tri varijable - konstantne funkcije f od (x, y, z) = 1 preko spomenutog područja između površine i ravni.) Ako postoji više varijabli, višestruki integral će dati hyper-zapreminu i višedimenzionalnu funkciju.

Višestruka integracija funkcija u $\;n$ varijablama: $\;f(x_{1},x_{2},\ldots ,x_{n})$ preko domena $\;D$ najčešće predstavlja postavljanje integralnih znakova u obrnutom redosledu rešavanja (krajnji levi integralni znak se izračunava zadnji) nastavljajući po funkciji i integrand argumentimaa u pravilnom redosledu (krajnji desni argument se izračunava zadnji). Domen integracije ili je zastupljena simbolično za svaki integrand preko svakog integralnog znaka, ili je često skraćen od strane varijable na krajnjem desnom integralnom znaku:

$\iint \ldots \int _{\mathbf {D} }\;f(x_{1},x_{2},\ldots ,x_{n})\;\mathbf {d} x_{1}\mathbf {d} x_{2}\!\ldots \mathbf {d} x_{n}$

Budući da je nemoguće izračunati antiderivative od funkcija sa više od jedne varijable, neodređeni višestruki integrali ne postoje. Zbog toga su svi višestruki integrali određeni integrali.

Primeri

Na primer, zapremina paralelopipeda stranica 4×6×5 može se izračunati na dva načina:

• Dvostrukim integralom

$\iint _{D}5\ dx\,dy\ \ [x=4,y=6\ \ \ \ z=5]$

funkcije f(x, y) = 5 izračunata u oblasti D u xy-ravni koja predstavlja bazu paralelopipeda.

• Trostrukim integralom

$\iiint _{\mathrm {paralelopiped} }1\,dx\,dy\,dz$

konstantne funkcije 1 izračunate na paralelopipedu.

Matematička definicija

Neka je n ceo broj veći od 1. Uzmimo takozvani poluotvoreni n-dimenzionalni pravougaonik (nazovimo ga jednostavno pravougaonik). Za ravan, N = 2, i višestruki integral je samo dvostruki integral.

$T=[a_{1},b_{1})\times [a_{2},b_{2})\times \cdots \times [a_{n},b_{n})\subset \mathbb {R} ^{n}.$

Podelimo svaki interval $[a_{i},b_{i})$ na određeni broj nepreklapajućih podintervala, sa svakim podintervalom zatvorenom na levom kraju, i otvorenom na desnom kraju. Označimo takve podintervale sa $I_{i}.$ Zatim, porodica podpravougaonika u obliku

$C=I_{1}\times I_{2}\times \cdots \times I_{n}$

je particija od $T,$ što daje podpravougaonike $C$ koji su nepreklapajući i njihova unija je $T.$.

Dijametri podpravougaonika $C$ su po definiciji najveće dužine intervala čiji proizvod je $C,$ u dijametru date particije od $T$ su definisane kao najveći diametri podpravougaonika u particiji.

Neka je $f:T\to \mathbb {R}$ funkcija definisana pravougaonikom $T.$ Razmotrimo particiju

$T=C_{1}\cup C_{2}\cup \cdots \cup C_{m}$

od $T$ definisanom iznad, gde je $m$ pozitivni integer. Rimanov zbir je zbir od oblika

$\sum _{k=1}^{m}f(P_{k})\,\operatorname {m} (C_{k})$

gde za svaku $k$ tačku $P_{k}$ je u $C_{k},$ i $\operatorname {m} (C_{k})$ je proizvod dužina intervala čiji Kartezijev proizvod je $C_{k}.$

Funkcija $f$ je Rimanski integrabilna ako je granica

$S=\lim _{\delta \to 0}\sum _{k=1}^{m}f(P_{k})\,\operatorname {m} \,(C_{k})$

postoji, gde je granica preuzela sve particije od $T$ od diametra najviše $\delta .$ Ako je $f$ Rimanski integrabilna, $S$ se zove Rimanskim integralom od $f$ nad $T,$ i označava se

$\int _{T}\!f(x)\,dx.$

Rimanski integral funkcije definisane nad proizvoljno omeđenom $n$-dimenzionalnom postavkom se može definisati proširivanjem te funkcije na funkciju definisanu preko poluotvorenog pravoganika čije vrednosti su nula izvan domena izvorne funkcije. Zatim, integral izvorne funkcije preko izvornog domena definiše se kao integral proširene funkcije nad njegovim pravougaonim domenom, ako postoji. Ono što sledi Riemannov integral u n dimenzijama će se zvati višestruki integral.

Osobine

Višestruki integrali imaju mnoge iste osobine integrala funkcija sa jednom varijablom (linearnost, aditivnost, monotoničnost, itd). Čak šta više, baš kao što je sa jednom promenljivom, može se koristiti višestruki integral da se pronađe prosek funkcije u datoj postavci. Još preciznije, za datu postavku $D\subset \mathbb {R} ^{n}$ i integrabilnu funkciju $f$ nad $D$, prosečna vrednost od $f$ nad njenim domenom je data sa

${\bar {f}}={\frac {1}{m(D)}}\int _{D}f(x)\,dx,$

gde je $\;m(D)$ mera od $\;D$.

Posebni slučajevi

U slučaju $T\subseteq \mathbb {R} ^{2},$ integral

$\ell =\iint _{T}f(x,y)\,dx\,dy$

je dvostruki integral od F na T, i ako $T\subseteq \mathbb {R} ^{3}$ integral

$\ell =\iiint _{T}f(x,y,z)\,dx\,dy\,dz$

je trostruki integral od F na T.

Onda, prema uobičajenom načinu obeležavanja u matematici, dvostruki integral ima dva integralna znaka, a trostruki integral ima tri, a to je samo zbog praktičnosti u označavanju, a zgodno je prilikom računanja višestrukih integrala kao ponovljenog integrala (kao što je prikazano u nastavku članka).

Metode integracije

Rešavanje problema s višestrukim integralima sastoji se (u većini slučajeva) u pronalaženju načina da se višestruki integral smanji u nizove integrala sa jednom varijablom, gde je svaki pojedinačno i direktno rešiv.

Direktno izračunavanje

Ponekad je moguće odrediti rezultat integracije bez ikakvih proračuna.

Konstante

U slučaju konstantne funkcije, rezultat je jednostavan: pomnoži se meru stalnom funkcijom c. Ako je c = 1, integriše se preko podregije od R² to daje prostor u regiji, dok je u R³ to je zapremina regije.

• Na primer:

$D=\{(x,y)\in \mathbb {R} ^{2}\ :\ 2\leq x\leq 4\ ;\ 3\leq y\leq 6\}$ and $f(x,y)=2\,\!$

Integriše se f od D:

$\int _{3}^{6}\int _{2}^{4}\ 2\ dx\,dy={\mbox{area}}(D)\cdot 2=(2\cdot 3)\cdot 2=12.$

Korištenje mogućih simetričnosti

U slučaju domena gde postoji simetrija poštujući barem jednu od osa i gde funkcija ima barem jedan paritet u odnosu na varijable, integral postaje ništavan (zbir suprotnih i jednakih vrednosti je nula). Dovoljno je da u funkcijama na Rⁿ zavisna promenljiva nije jednaka sa osama simetrije.

• Primer (1):

S obzirom da je $f(x,y)=2\ \sin(x)-3\ y^{3}+5$ i $T=x^{2}+y^{2}\leq 1$ je integralno područje (disk sa radijusom 1 u središtu preseka osa, granica uključena).

Korištenjem svojstva linearnosti, integral se može rastaviti u tri dela:

$\iint _{T}(2\ \sin(x)-3\ y^{3}+5)\ dx\,dy=\iint _{T}2\ \sin(x)\ dx\,dy-\iint _{T}3\ y^{3}\ dx\ dy+\iint _{T}5\ dx\ dy$

2 sin(x) i 3y³ su obe neparne funkcije i štaviše očito je da T disk ima simetriju za x, pa čak i y osu, dakle jedini doprinos konačnom rezultatu integrala je ta od stalne funkcije 5, jer su ostala dva komada nula.

• Primer (2):

Razmotrimo funkciju $f(x,y,z)=x\ e^{y^{2}+z^{2}}$ i kao integraciono područje - sfera sa radiusom 2 i središtem u preseku osa $T=x^{2}+y^{2}+z^{2}\leq 4$. „Lopta” je simetrična oko sve tri ose, ali to je dovoljno da se integrišu s obzirom na x-osu da se pokaže da je integral 0, jer je funkcija neparna funkcija te varijable.

Formule redukcije (smanjenja)

Formule smanjenja koriste koncept jednostavnog domena da se omogući raščlanjivanje višestrukog integrala kao proizvoda drugih jednovarijabilnih integrala. Ovi se moraju rešiti s desna na levo s obzirom na druge varijable kao konstante (što je isti postupak kao pri računanju parcijalne derivacije).

Normalni domeni na R²

x-osa

Ako je D merljiv domen okomit na x-osu i $f:D\longrightarrow \mathbb {R}$ je kontinuirana funkcija; onda su α(x) i β(x) (definisane u [a,b] intervalu) dve funkcije koje određuju D. Onda je:

$\iint _{T}f(x,y)\ dx\,dy=\int _{a}^{b}dx\int _{\alpha (x)}^{\beta (x)}f(x,y)\,dy\ \ (normalitet\ \ u\ \ odnosu\ \ na\ \ x\ \ osu).$

y-osa

Ako je D merljiv domen okomit na y-osu i $f:D\longrightarrow \mathbb {R}$ je kontinuirana funkcija; onda su α(y) i β(y) (definisani u [a,b] intervalu) su dve funlcije koje određuju D. Onda je:

$\iint _{T}f(x,y)\ dx\,dy=\int _{a}^{b}dy\int _{\alpha (y)}^{\beta (y)}f(x,y)\,dx\ \ (normalitet\ \ u\ \ odnosu\ \ na\ \ y\ \ osu).$

Primer: D područje za integral po formulama redukcije.

Primer

Razmotrimo ovo područje: $D=\{(x,y)\ :\ x=0,x=1,y=x^{2},y=1\}\ ;\int _{0}^{1}(\int _{x^{2}}^{1}1\,dy)\,dx.$ (pogledati grafik primera). Može se izračunati

$\iint _{D}f(x,y)\,dx\,dy.$

Ovaj domen je okomit na obe x i y ose. Za primenu formule moraju se pronaći funkcije koje određuju D, i njegovu intervalnu definiciju. U ovom slučaju dve funkcije su:

$\alpha (x)=f(x)=y=x^{2}\,\!$ and $\beta (x)=y=1\,\!$

dok je interval dobijen iz ukrštanja funkcija sa $x=0\,\!$, tako da je interval $[a,b]=[0,1]\,\!$ (normalitet u odnosu na x-osu je izabran zbog boljeg vizualnog razumevanja).

Sad je moguće primeniti formule:

$\iint _{D}f(x,y)\,dx\,dy=\int _{0}^{1}(\int _{x^{2}}^{1}1\,dy)\,dx=\int _{0}^{1}\left[y\right]_{x^{2}}^{1}\,dx=\int _{0}^{1}(1-x^{2})\,dx$

(Prvo se izračunava unutrašnji integral uzimajući x kao konstantu). Preostale operacije se sastoje od primenjivanja osnovnih tehnika integracije:

$\int _{0}^{1}(1-x^{2})\,dx=\int _{0}^{1}\,dx-\int _{0}^{1}x^{2}\,dx=\left[x\right]_{0}^{1}-\left[{\frac {x^{3}}{3}}\right]_{0}^{1}=(1-0)-{\frac {1}{3}}\left[\ x^{3}\right]_{0}^{1}=1-{\frac {1}{3}}(1-0)=1-{\frac {1}{3}}={\frac {2}{3}}$

${\frac {2}{3}}=[x*y=x*x^{2}=x^{3}(pravougaonik\ \ -\ \ ovde\ \ kvadrat)-{\frac {x^{3}}{3}}(parabola\ \ iznad\ \ x\ \ ose);(x=1)].$

Ako se izabere normalitet u odnosu na y-osu može se izračunati

$D=\{(x,y)\ :\ y=0,y=1,x=0,x={\sqrt {y}}\}\ ;\int _{0}^{1}(\int _{0}^{\sqrt {y}}1\,dx)\,dy.$

i dobiti ista vrednost.

$\iint _{D}f(x,y)\,dx\,dy=\int _{0}^{1}(\int _{0}^{\sqrt {y}}1\,dx)\,dy=\int _{0}^{1}\left[x\right]_{0}^{\sqrt {y}}\,dy=\int _{0}^{1}({\sqrt {y}}-0)\,dy=\left[{\frac {2}{3}}y^{\frac {3}{2}}\right]_{0}^{1}={\frac {2}{3}}(1-0)={\frac {2}{3}}$

${\frac {2}{3}}=[x*y=x*x^{2}=x^{3}(pravougaonik\ \ -\ \ ovde\ \ kvadrat)-{\frac {x^{3}}{3}}(parabola\ \ iznad\ \ x\ \ ose);(x=1)].$

Primer normalnog domena u R3 (xy-ravni).

Normalni domeni na R³

Proširenje ovih formula na trostruke integrale bi trebalo biti očigledno: T je domen okomit na xy-ravan u odnosu na α (x,y,z) i β(x,y,z) funkcije. Onda je:

$\iiint _{T}f(x,y,z)\ dx\,dy\,dz=\iint _{D}dx\,dy\int _{\alpha (x,y,z)}^{\beta (x,y,z)}f(x,y,z)\,dz$

(ova definicija je ista za ostalih 5 slučajeva normaliteta na R³).

Promena varijabli

Granice integracije često nisu lako zamenljive (bez normaliteta ili sa složenim formulama da se integrišu), može se uraditi promenu varijabli i prepisati integral u „boljem” području, što može biti opisano u jednostavnijim formulama. Da bi se to učinilo, funkcija mora biti prilagođena novim koordinatama.

Primer (1-a):

Funkcija je $f(x,y)=(x-1)^{2}+{\sqrt {y}}$;

ako se usvoji ova zamenu $x'=x-1,\ y'=y\,\!$ onda je $x=x'+1,\ y=y'\,\!$

dobija se nova funkcija $f_{2}(x,y)=(x')^{2}+{\sqrt {y}}$.

• Slično za domen jer je omeđen izvornim varijablama koje su pretvorene pre u ( x i y primeru).
• diferencijali dx i dy transformirani preko matrice Jakobijeve determinante sadrži parcijalne derivacije transformacija u odnosu na novu varijablu (uzeti u obzir kao primer, diferencijalnu transformaciju u polarnim koordinatama). Postoje tri glavne „vrste” promena varijabli (jedna u R², druga u R³); međutim, pogodna zamena se može naći pomoću istog principa na uopšteniji način.

Polarne koordinate

Glavni članak: Polarni koordinatni sistem

Promena od kartezijevih u polarne koordinate.

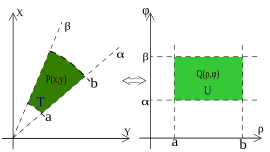
U R² ako domen ima kružnu „simetriju”, a funkcija ima neke „posebne” karakteristike može se primeniti transformacija na polarnim koordinatama (vidi primer na slici), što znači da se tačke P (x, y) u Kartezijevim koordinatama mogu preneti na njihova mesta u polarnim koordinatama. To omogućuje da se promeni „oblik” u domenu i pojednostave operacije.

Temeljni odnos da bi uradili transformaciju je sledeći:

$f(x,y)\rightarrow f(\rho \ \cos \phi ,\rho \ \sin \phi ).$

Primer (2-a)

Funkcija je $f(x,y)=x+y\,\!$

i primenom transformacije se dobija

$f(\rho ,\phi )=\rho \cos \phi +\rho \sin \phi =\rho \ (\cos \phi +\sin \phi ).$

Primer (2-b)

Funkcija je $f(x,y)=x^{2}+y^{2}\,\!$ U ovom slučaju je:

$f(\rho ,\phi )=\rho ^{2}(\cos ^{2}\phi +\sin ^{2}\phi )=\rho ^{2}\,\!$

koristeći Pitagorin trigonometrijski identitet (veoma koristan u pojednostavljivanju ove operacije). Promena domena je urađena kroz definisanje glavne dužine radijusa i amplitude opisanog ugla da bi definisali ρ, φ intervale počevši od x, y.

Primer promene domena od kartezijevog ka polarnom.

Primer (2-c)

Domen je $D=x^{2}+y^{2}\leq 4\,\!$, da je opseg radijusa 2, očito je da je pokriveni ugao kružni ugao, tako da φ varira od 0 do 2π, dok glavni radijus varira 0-2 (kruna s unutrašnjim radijusom nula je samo krug).

Primer (2-d)

Domen je $D=\{x^{2}+y^{2}\leq 9,\ x^{2}+y^{2}\geq 4,\ y\geq 0\}$, da je kružna kruna u pozitivnom delu y poluravnine (pogledajte sliku u primjeru); napomena da φ opisuje ugao ravnine dok ρ varira dva-tri. Stoga promena domena će biti sledeći pravougaonik:

$T=\{2\leq \rho \leq 3,\ 0\leq \phi \leq \pi \}$.

Jakobijeva determinanta ove transformacije je sledeća:

${\frac {\partial (x,y)}{\partial (\rho ,\phi )}}={\begin{vmatrix}\cos \phi &-\rho \sin \phi \\\sin \phi &\rho \cos \phi \end{vmatrix}}=\rho$

koji je dobijen umetanjem parcijalne derivacije x = ρ cos (φ), y = ρ sin (φ) u prvom redu u odnosu na ρ i u drugom u odnosu na φ, tako da dx dy diferencijacije u ovoj transformaciji postaje ρdρdφ.

Nakon što se funkcija transformiše i domen vrednuje, moguće je definisati formulu za promenu varijabli u polarnim koordinatama:

$\iint _{D}f(x,y)\ dx\,dy=\iint _{T}f(\rho \cos \phi ,\rho \sin \phi )\rho \,d\rho \,d\phi .$

Treba imati na umu da φ vredi u [0, 2π] intervalu, dok ρ, jer je to mera dužine, može imati samo pozitivne vrednosti.

Primer (2-e)

Funkcija je $f(x,y)=x\,\!$, a domen je isti kao u 2-D primeru. Iz prethodne analize D znaju se intervali od ρ (2 do 3) i φ (od 0 do π). Funkcija se može promeniti na sledeći način:

$f(x,y)=x\longrightarrow f(\rho ,\phi )=\rho \ \cos \phi .$

i se primenjuje formula integracije:

$\iint _{D}x\,dx\,dy=\iint _{T}\rho \cos \phi \ \rho \,d\rho \,d\phi .$

Nakon što su intervali poznati, dobija se

$\int _{0}^{\pi }\int _{2}^{3}\rho ^{2}\cos \phi \ d\rho \ d\phi =\int _{0}^{\pi }\cos \phi \ d\phi \left[{\frac {\rho ^{3}}{3}}\right]_{2}^{3}=\left[\sin \phi \right]_{0}^{\pi }\ \left(9-{\frac {8}{3}}\right)=0.$

Cilindrične koordinate

Cilindrične koordinate.

U R³ integracija na domenima s kružnom osnovom može se uraditi prolazom na cilindrične koordinate; transformacija funkcije se vrši prema sledećem odnosu:

$f(x,y,z)\rightarrow f(\rho \ \cos \phi ,\rho \ \sin \phi ,z)$

Transformacija domena se može grafički postići, jer samo oblik baze varira, a visina sledi oblik početne regije.

Example (3-a)

Region je $D=\{x^{2}+y^{2}\leq 9,\ x^{2}+y^{2}\geq 4,\ 0\leq z\leq 5\}$ (to je „cev” čija je osnovica kružna kruna i čija visina je 5), ako je transformacija primenjena, za ovo područje se dobija: $T=\{2\leq \rho \leq 3,\ 0\leq \phi \leq \pi ,\ 0\leq z\leq 5\}$ (to je paralelopiped čija osnova je pravougaonik u 2-d primer i čija visina je 5).

Zbog toga što se z komponenta ne menja tokom transformacije, i dx dy dz diferencijali se razlikuju kao u prolazu u polarnim koordinatama: dakle, oni postaju ρ dρ dφ dz.

Konačno, moguće je primeniti završnu formulu u cilindričnim koordinatama:

$\iiint _{D}f(x,y,z)\,dx\,dy\,dz=\iiint _{T}f(\rho \cos \phi ,\rho \sin \phi ,z)\rho \,d\rho \,d\phi \,dz.$

Ova metoda je prikladna kod cilindričnih ili konusnih domena ili u područjima gde je lako izdvojiti z interval, pa čak i transformisati kružnu osnovicu i funkciju

Primjer (3-b)

Funkcija je $f(x,y,z)=x^{2}+y^{2}+z\,\!$ i kao domen integracije ovog cilindra: :$D=\{x^{2}+y^{2}\leq 9,\ -5\leq z\leq 5\}$. Transformacija D u cilindričnim koordinatama je sledeća:

$T=\{0\leq \rho \leq 3,\ 0\leq \phi \leq 2\pi ,\ -5\leq z\leq 5\}.$

dok funkcija postaje

$f(\rho \ \cos \phi ,\rho \ \sin \phi ,z)=\rho ^{2}+z\,\!$

Konačno može se primeniti formulu integracije:

$\iiint _{D}(x^{2}+y^{2}+z)\,dx\,dy\,dz=\iiint _{T}(\rho ^{2}+z)\rho \,d\rho \,d\phi \,dz;$

razvijajući formulu se dobija

$\int _{-5}^{5}dz\int _{0}^{2\pi }d\phi \int _{0}^{3}(\rho ^{3}+\rho z)\,d\rho =2\pi \int _{-5}^{5}\left[{\frac {\rho ^{4}}{4}}+{\frac {\rho ^{2}z}{2}}\right]_{0}^{3}\,dz$

$=2\pi \int _{-5}^{5}\left({\frac {81}{4}}+{\frac {9}{2}}z\right)\,dz=\cdots =855\pi .$

Sferne koordinate

Sferne koordinate.

U R³ neki domeni imaju sfernu simetriju, tako da je moguće odrediti koordinate svake tačke integracije regije dva ugla i jedne udaljenosti. Te je stoga moguće koristiti prolaz u sferne koordinate; funkcija je promenjena ovim odnosom:

$f(x,y,z)\longrightarrow f(\rho \cos \theta \sin \phi ,\rho \sin \theta \sin \phi ,\rho \cos \phi )\,\!$

Treba imati na umu da tačke na z osi nemaju preciznu karakterizaciju u sfernim koordinatama, tako da je za tacke polova - $\phi$ = 0 ili π (inače može varirati između 0 i π).

Očigledno je da je sfera bolji domen integracije za ovaj prolaz.

Primer (4-a)

Domen je $D=x^{2}+y^{2}+z^{2}\leq 16$ (sfera sa radijusom 4 i centrom u osnovici); uvođenjem transformacije dobijamo područje: $T=\{0\leq \rho \leq 4,\ 0\leq \phi \leq 2\pi ,\ 0\leq \theta \leq \pi \}.$

Jakobijeva determinanta ove transformacije je sledeća:

${\frac {\partial (x,y,z)}{\partial (\rho ,\theta ,\phi )}}={\begin{vmatrix}\cos \theta \sin \phi &-\rho \sin \theta \sin \phi &\rho \cos \theta \cos \phi \\\sin \theta \sin \phi &\rho \cos \theta \sin \phi &\rho \sin \theta \cos \phi \\\cos \theta &-\rho \sin \theta &0\end{vmatrix}}=\rho ^{2}\sin \theta$

dx dy dz diferencijali su onda transformisani u ρ² sin(θ) dρ dθ dφ.

Konačno dobija se završna formula integracije:

$\iiint _{D}f(x,y,z)\,dx\,dy\,dz=\iiint _{T}f(\rho \sin \theta \cos \phi ,\rho \sin \theta \sin \phi ,\rho \cos \theta )\rho ^{2}\sin \theta \,d\rho \,d\theta \,d\phi .$

Bolja integracija domena za ovaj prolaz očito se dobija upotrebom sfere. Bolje je koristiti ovu metodu u slučaju sfernih domena i u slučaju funkcija koje se mogu lako pojednostaviti, sa prvim temeljnim odnosom trigonometrije, produženim u R³ (pogledajte primer 4-b); u drugim slučajevima bolje je koristiti cilindrične koordinate (pogledajte primer 4-c).

$\iiint _{T}f(a,b,c)\rho ^{2}\sin \theta \,d\rho \,d\theta \,d\phi .$

Treba imati na umu da dodatne $\rho ^{2}$ i $\sin \theta$ dolaze od Jakobijeve determinante.

Primer (4-b)

D je isto područje iz primera 4-a i $f(x,y,z)=x^{2}+y^{2}+z^{2}\,\!$ je funkcija koja se integriše.

Njena transformacija je veoma jednostavna:

$f(\rho \sin \theta \cos \phi ,\rho \sin \theta \sin \phi ,\rho \cos \theta )=\rho ^{2},\,$

dok znamo intervale transformisanog područja

T od D:

$(0\leq \rho \leq 4,\ 0\leq \phi \leq 2\pi ,\ 0\leq \theta \leq \pi ).\,$

Stoga se može primeniti formula integracije:

$\iiint _{D}(x^{2}+y^{2}+z^{2})\,dx\,dy\,dz=\iiint _{T}\rho ^{2}\ \rho ^{2}\sin \theta \,d\rho \,d\theta \,d\phi ,$

i razvijanjem se dobija:

$\iiint _{T}\rho ^{4}\sin \theta \,d\rho \,d\theta \,d\phi =\int _{0}^{\pi }\sin \theta \,d\theta \int _{0}^{4}\rho ^{4}d\rho \int _{0}^{2\pi }d\phi =2\pi \int _{0}^{\pi }\sin \theta \left[{\frac {\rho ^{5}}{5}}\right]_{0}^{4}\,d\theta$

$=2\pi \left[{\frac {\rho ^{5}}{5}}\right]_{0}^{4}\left[-\cos \theta \right]_{0}^{\pi }=4\pi \cdot {\frac {1024}{5}}={\frac {4096\pi }{5}}.$

Primer (4-c)

Domen D je lopta sa centrom u osnovi i radijusom 3a ($D=x^{2}+y^{2}+z^{2}\leq 9a^{2}\,\!$) i $f(x,y,z)=x^{2}+y^{2}\,\!$ je funkcija koja se integriše.

Gledajući na domen, čini se prikladnim da se prihvati prelaz na sferne koordinate, zapravo intervali varijabli koje razgraničavaju novo T područje su očito:

$0\leq \rho \leq 3a,\ 0\leq \phi \leq 2\pi ,\ 0\leq \theta \leq \pi .\,$

Međutim, uvodeći transformaciju dobija se

$f(x,y,z)=x^{2}+y^{2}\longrightarrow \rho ^{2}\sin ^{2}\theta \cos ^{2}\phi +\rho ^{2}\sin ^{2}\theta \sin ^{2}\phi =\rho ^{2}\sin ^{2}\theta$.

Primjenjujući formulu za integraciju dobija se:

$\iiint _{T}\rho ^{2}\sin ^{2}\theta \rho ^{2}\sin \theta \,d\rho \,d\theta \,d\phi =\iiint _{T}\rho ^{4}\sin ^{3}\theta \,d\rho \,d\theta \,d\phi$

koju je veoma teško rešiti. Ovaj problem će se rešiti koristeći prolaz u cilindričnim koordinatama. Novi T intervali su

$0\leq \rho \leq 3a,\ 0\leq \phi \leq 2\pi ,\ -{\sqrt {9a^{2}-\rho ^{2}}}\leq z\leq {\sqrt {9a^{2}-\rho ^{2}}};$

z interval je bio dobijen deljenjem lopte na dve hemisfere jednostavno rešavanjem nejednakosti iz formule od D (a zatim direktno menjajući x² + y² u ρ²). Nova funkcija je jednostavno ρ². Primenjujući formulu integracije

$\iiint _{T}\rho ^{2}\rho \ d\rho d\phi dz$.

Zatim se dobija

$\int _{0}^{2\pi }d\phi \int _{0}^{3a}\rho ^{3}d\rho \int _{-{\sqrt {9a^{2}-\rho ^{2}}}}^{\sqrt {9a^{2}-\rho ^{2}}}\,dz=2\pi \int _{0}^{3a}2\rho ^{3}{\sqrt {9a^{2}-\rho ^{2}}}\,d\rho .$

Sad se primenjuje transformacija

$9a^{2}-\rho ^{2}=t\,\!\longrightarrow dt=-2\rho \,d\rho \longrightarrow d\rho ={\frac {dt}{-2\rho }}\,\!$

(novi intervali postaju $0,3a\longrightarrow 9a^{2},0$). Dobija se

$-2\pi \int _{9a^{2}}^{0}\rho ^{2}{\sqrt {t}}\,dt$

je $\rho ^{2}=9a^{2}-t\,\!$, dobija se

$-2\pi \int _{9a^{2}}^{0}(9a^{2}-t){\sqrt {t}}\,dt,$

nakon preokretanja granica integracije i množenjem uslova između zagrada, moguće je rastaviti integral u dva dela koji se mogu direktno rešiti:

$2\pi \left[\int _{0}^{9a^{2}}9a^{2}{\sqrt {t}}\,dt-\int _{0}^{9a^{2}}t{\sqrt {t}}\,dt\right]=2\pi \left[9a^{2}{\frac {2}{3}}t^{\frac {3}{2}}-{\frac {2}{5}}t^{\frac {5}{2}}\right]_{0}^{9a^{2}}$

$=2\cdot 27\pi a^{5}(6-{\frac {2}{5}})=54\pi {\frac {28}{5}}a^{5}={\frac {1512\pi }{5}}a^{5}.$

Zahvaljujući prolazu u cilindričnim koordinatama bilo je moguće svesti trostruki integral na lakši jednovarijabilni integral. Pogledati takođe ulaz razlika u zapremini nabla u cilindričnim i sfernim koordinatama.

Primer matematičke primene - izračunavanje zapremine

Zahvaljujući prethodno opisanim metodama moguće je odrediti zapreminu nekih tela.

• Cilindar: Zamislimo oblast integracije kao kružnu bazu poluprečnika R i konstantnu funkciju kao konstantu na visini h. Moguće je ovo zapisati u polarnim koordinatama na ovaj način:

$\mathrm {Zapremina} =\int _{0}^{2\pi }d\phi \int _{0}^{R}h\rho \ d\rho =h2\pi \left[{\frac {\rho ^{2}}{2}}\right]_{0}^{R}=\pi R^{2}h$

Provera: Zapremina = površina baze * visina = $\pi R^{2}\cdot h$

• Sfera: Za ovaj primer mogu se upotrijebiti sferne koordinate na konstantnu integracionu funkciju 1 na sferi istog poluprečnika R:

$\mathrm {Zapremina} =\int _{0}^{2\pi }\,d\phi \int _{0}^{\pi }\sin \theta \,d\theta \int _{0}^{R}\rho ^{2}\,d\rho =2\pi \int _{0}^{\pi }\sin \theta {\frac {R^{3}}{3}}\,d\theta ={\frac {2}{3}}\pi R^{3}[-\cos \theta ]_{0}^{\pi }={\frac {4}{3}}\pi R^{3}.$

• Tetraedar (trouglasta piramida ili 3-simpleks): Zapremina tetraedra iznosi:

$\mathrm {Zapremina} =\int _{0}^{\ell }dx\int _{0}^{\ell -x}\,dy\int _{0}^{\ell -x-y}\,dz=\int _{0}^{\ell }dx\int _{0}^{\ell -x}(\ell -x-y)\,dy$

$=\int _{0}^{\ell }(\ell ^{2}-2\ell x+x^{2}-{\frac {(\ell -x)^{2}}{2}})\,dx=\ell ^{3}-\ell \ell ^{2}+{\frac {\ell ^{3}}{3}}-\left[{\frac {\ell ^{2}}{2}}-\ell x+{\frac {x^{2}}{2}}\right]_{0}^{\ell }=$

$={\frac {\ell ^{3}}{3}}-{\frac {\ell ^{3}}{6}}={\frac {\ell ^{3}}{6}}$

Provera: Zapremina = površina baze × visina/3 = ${\frac {\ell ^{2}}{2}}\cdot \ell /3={\frac {\ell ^{3}}{6}}.$

Primer loše definisane oblasti integracije.

Višestruki nepravilni integral

U slučaju slobodnih domena ili neograđenih funkcija u blizini granice domena, mora se uvesti dvostruki nesvojstveni integral ili trostruki nepravilni integral.

Višestruki integrali i iterativni integrali

Fubinijeva teorema kaže da ako je

$\int _{A\times B}|f(x,y)|\,d(x,y)<\infty ,$

tada je integral apsolutno konvergentan, i tada će višestruki integral dati isti rezultat kao iterativni integral,

$\int _{A\times B}f(x,y)\,d(x,y)=\int _{A}\left(\int _{B}f(x,y)\,dy\right)\,dx=\int _{B}\left(\int _{A}f(x,y)\,dx\right)\,dy.$

To će se posebno dogoditi ako $|f(x,y)|$ je ograničena funkcija i A i B ograničeni skupovi.

Ako integral nije apsolutno konvergentan, potrebno je paziti da se ne mešaju pojmovi višestruki integral i iterativni integral, pogotovo jer se isto označavanje često koristi za obe koncepcije. Označavanje

$\int _{0}^{1}\int _{0}^{1}f(x,y)\,dy\,dx$

znači u nekim slučajevima, iterativni integral radije nego pravi dvostruki integral. U iterativnom integralu, vanjski integral

$\int _{0}^{1}\cdots \,dx$

je integral u odnosu na x u sledećoj funkciji od x:

$g(x)=\int _{0}^{1}f(x,y)\,dy.$

Dvostruki integral, s druge strane, definisan je s obzirom na područje u xy-ravni. Ako dvostruki integral postoji, onda je jednak za svaki od dva iterativna integrala (ili dy dx ili dx dy) i često se izračunava izračunavajući pojedinačno svaki iterativni integral. Ponekad dva iterativna integrala postoje kad dvostruki integral ne postoji, a u nekim slučajevima su dva iterativna integrala različiti brojevi, tj. jedan ima

$\int _{0}^{1}\int _{0}^{1}f(x,y)\,dy\,dx\neq \int _{0}^{1}\int _{0}^{1}f(x,y)\,dx\,dy.$

Ovo je primer preuređenja uslovne konvergencije integrala.

Označavanje

$\int _{[0,1]\times [0,1]}f(x,y)\,dx\,dy$

može se koristiti ako je cilj da se pojasni namera pri primeni dvostrukog integrala.

Neke praktične primene

Ovi integrali se koriste u mnogim aplikacijama u fizici.

U mehanici moment inercije se izračunava kao zapremina integrala (koji je trostruki integral) od gustine u odnosu na kvadrat udaljenosti od ose:

$I_{z}=\int _{V}^{.}\rho r^{2}\,dV.$

U elektromagnetizmu, Maksvelova jednačina se može napisati pomoću višestrukih integrala za izračunavanje ukupnog magnetnog i električnog polja. U sledećem primeru, električno polje proizvedeno distribucijom napona je izraženo putem trostrukog integrala vektorske funkcije:

${\vec {E}}={\frac {1}{4\pi \epsilon _{0}}}\int {\frac {{\vec {r}}-{\vec {r}}'}{\left\|{\vec {r}}-{\vec {r}}'\right\|^{3}}}\rho ({\vec {r}}')\,\operatorname {d} ^{3}r'.$

Vidi još

• Teorema divergencije
• Stoksova teorema
• Grinova teorema

Literatura

• Adams, Robert A. Calculus: A Complete Course (5th изд.). ISBN 978-0-201-79131-0. 
• Jain, R. K.; Iyengar, S. R. K. (2009). Advanced Engineering Mathematics (3rd изд.). Narosa Publishing House. ISBN 978-81-7319-730-7. 

Spoljašnje veze

• Weisstein, Eric W. „Multiple Integral”. MathWorld. 
• L.D. Kudryavtsev (2001) [1994], „Multiple integral”, Ур.: Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4 
• Mathematical Assistant on Web online evaluation of double integrals in Cartesian coordinates and polar coordinates