Механички рад

За друге употребе, погледајте Рад (вишезначна одредница).

Рад
Бацач у бејзболу позитивно делује на лопту примењујући на њу силу на растојању на коме се креће.
Уобичајени симболи	W
СИ јединица	џул (J)
Друге јединице	стопа-фунта, [[Erg]]
У СИ базним јединицама	1 kg⋅m2⋅s−2
СИ димензија	M L2 T−2
Деривације из других квантитета	W = F ⋅ s W = τ θ

Рад у физици је пренос енергије из једног система у други. Овај пренос се у класичној механици врши деловањем силе дуж неког пута. Рад је у ствари једнак производу силе и пређеног пута, ако сила делује у правцу померања тела. У пољу конзервативне силе рад не зависи од облика пута, већ само од почетне и крајње тачке.

Рад је скаларна величина. Јединица за рад у Међународном систему јединица је џул (J), који представља:

$\mathrm {J={\frac {kg\,m^{2}}{s^{2}}}}$

Физичку величину производа силе и дужине је у физику увео научник Гаспар Гистав Кориолис 1830-их.

Математичка дефиниција

Једноставнији облик дефиниције рада је сведен на претпоставку константне вредности силе и праволинијске путање. Тада се механички рад може дефинисати као скаларни производ вектора силе и вектора помераја.

$A={\vec {F}}\cdot {\vec {r}}$

Претходно поменута дефиниција рада има своја ограничења. Она важи под условом да је сила константна, а путања тела није кривудава. Стога је потребно увести математички правилнију дефиницију, која се заснива на идеји да се кривудава путња подели на велики број мањих, апоскримативно правих делова делова. Отуда се добија образац:

$A\approx \sum _{i=1}^{N}A_{i}=\sum _{i=1}^{N}{\vec {F}}(\mathbf {s} _{i})\Delta {\vec {s}}_{i}\,.$

Одакле:

$A=\int _{\mathbf {s} _{1}}^{\mathbf {s} _{2}}{\vec {F}}(\mathbf {s} )\,\mathrm {d} {\vec {s}}\,,$

Из горње једначине следи да је рад ($A\,$) једнак интегралу скаларног производа вектора силе (${\vec {F}}$) и инфинитезимале вектора пута (${\vec {s}}$).

Однос снаге и рада

Рад се може рачунати и као производ снаге и времена :

$A=P\cdot t$

Ово важи у ситуацији када је снага непроменљива током времена.

Пример

У овом примеру сила и смер (путања тела) су колинеарни. Претпоставимо да се камен масе 10 kg налази на тлу, и да треба да га подигнемо вертикално увис до висине h = 1,5 m. Убрзање силе теже g = 9,81 m/s².

m = 10 kg

h = 1,5 m

g = 9,81 m/s²

Сила гравитације F која делује на камен је:

$F=m\cdot g=10\cdot 9,81=98,1N$

Одатле, уложени рад при подизању камена се добија као:

$A=F\cdot h=98,1\cdot 1,5=147,15J$

Специјални случај „сила пута пут”

Најједноставнија формула за рад силе, која је најбоље полазиште за разумевање појма рада, вреди нпр. у случају када константна сила делује на тело које се транслацијски (тј. без ротације) креће у смеру њеног деловања. Тада је (као што произлази и из горњег интеграла):

$W=Fs\,$

gdje je F iznos sile, dok je s pređeni put. Na taj se slučaj odnosi definicija iz osnovne škole "rad je sila puta put", koja ne uzima u obzir da je sila vektor (što je ovdje irelevantno zato što su i sila i gibanje u istom smjeru koji se ne mijenja), niti precizira da treba promatrati put hvatišta sile (jer se sve točke tijela jednako gibaju, pa može biti i "put tijela"). Npr. ako sila od 5 N vuče tijelo na putu od 3 m, ona izvrši rad W = Fs = 5 N ∙ 3 m = 15 J. Odatle se vidi da je SI mjerna jedinica za rad, džul (J), skraćenica za umnožak "Nm".

Ipak, ova jednostavna formula nije ograničena samo na pravocrtno gibanje. Ona vrijedi uvijek kada se iznos sile ne mijenja, a hvatište sile se giba točno u smjeru djelovanja sile (koji se može po volji mijenjati).

Закон о промени кинетичке енергије

Однос рада и промене енергије кључна је одредница за разумевање дефиниције рада силе. Ако је у претходном једноставном примеру сила F једина сила која делује на тело масе m које је до тада мировало (није имало кинетичке енергије), тело на путу s има стално убрзање a = F/m и креће се једнолико убрзано, те на крају путa s = at²/2 постиже брзину v = at. Одатле се лако види да је рад силе једнак кинетичкој енергији коју тело добије на том путу:

$W=Fs=ma{\frac {at^{2}}{2}}=m{\frac {(at)^{2}}{2}}={\frac {mv^{2}}{2}}=E_{k}$

Поопштење тог резултата (могло би се добити из опште формуле за рад силе, уз мало више рачуна) зове се закон о промени кинетичке енергије: рад свих сила које делују на круто тело једнак је промени његове кинетичке енергије. Притом треба имати на уму да кинетичка енергија тела не мора бити само транслацијска (како је описана у горњем једноставном примеру), него може имати и ротацијски део (осим у случају честице, тј. тела занемаривих димензија).

Објашњење дефиниције рада силе

Објашњење опште формуле за рад силе полази од описане везе с енергијом: формула је конструирана управо тако да промена кинетичке енергије буде једнака укупном раду свих сила.

Значај тангенцијалне компоненте силе

Декомпозиција силе на тангенцијалну и нормалну векторску компоненту

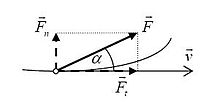
Прва последица те везе јесте да сила која делује на честицу окомито на смер њеног кретања (каже се: нормална сила; пример: центрипетална сила) не врши рад - јер не мења износ брзине (него само њен смер) те не утиче на кинетичку енергију честице. Сила која лежи на правцу кретања честице (каже се: тангенцијална сила) врши позитиван рад ако је у смеру кретања, јер повећава брзину а тиме и кинетичку енергију честице, односно негативан рад ако је у супротном смеру од кретања, јер умањује кинетичку енергију. Зато се произвољни вектор силе ^{$\scriptstyle {\vec {F}}$} прикаже као збир тангенцијалне и нормалне силе (формалније речено: растави на тангенцијалну и нормалну векторску компоненту), од чега се за прорачун рада користи само тангенцијална. Притом је F cos α тангенцијална скаларна компонента вектора силе ^{$\scriptstyle {\vec {F}}$}, тј. то је број који је једнак износу тангенцијалне векторске компоненте силе ако је она у смеру кретања, односно њезином негативном износу ако је у супротном смеру (што даје и одговарајући предзнак рада).

Улога хватишта силе

Рачунање рада помоћу пута који прелази хватиште силе (док друге тачке тела могу прелазити различите путеве) такође је последица описане везе с енергијом. Сила при тој брзини се рачуна као транслацијска кинетичка енергија тела. Ако правац деловања силе не пролази кроз центар масе, осим описаног учинка сила даје телу и угаоно убрзање α, те му мења и ротацијску кинетичку енергију. Тада сила мора вршити већи рад него кад делује на центар маса, а то се дешава зато што њено хватиште прелази већи пут него што је пут центар маса (тј. „пут тела”). Закон полуге још јасније доказује да се рад силе рачуна помоћу пута хватишта силе: на већем краку довољна је мања сила за исти рад зато што њено хватиште прелази већи пут.

Промењиву силу треба интегрисати

Рад силе се може израчунати као умножак два броја (компоненте F cos α и пута њезинога хватишта s) само ако се зна колико ти бројеви износе, тј. ако се на одабраном путу тангенцијална скаларна компонента силе не мења. Но, у општем случају сила може произвољно мењати износ и смер: тада се рад мора рачунати помоћу интеграла, јер не постоји једноставнији поступак да се одреди просечна вредност F cos α за рачунање рада на неком путу.

Тумачење и пример интеграла рада

Поступак интегрисања може се најлакше разумети као замсли да се сабирају радови проматране силе по врло малим комадима укупнога пута, тако малима да се сила на поједином комадићу „не стигне” да се промени. Наравно, све док је број комадића коначан, сила ће се на свакоме бар мало променити (ако се стално мења), али та промена може бити у тако далекој децимали да је то у коначном резултату занемарљиво (те се узима било која вредност с појединог комадића пута). Ако то није случај, пут се може подијелити у још ситније комадиће пре збрајања радова, све док не добије резултат који је тачан у жељеном броју децималних места (што се проверава поређењем с наредном још ситнијом раздеобом пута). Такав се поступак зове нумеричко интегрисање.

Процес уситњавања се може мисаоно наставити у недоглед, знајући да се тако добијају узастопни резултати са све већим бројем тачних цифара. Интеграл је (ако постоји) онај број (гранична вредност или лимес) којим се ти узастопни збирови све мањих комадића рада све више приближавају (уз довољно уситњавање пута, зброј радова је по вољи близу граничне вредности). А како показује математичка анализа, та тачна гранична вредност се може за многе конкретне силе израчунати на посве другачији начин, помоћу правила интегрисања за поједине врсте функција. На пример, рад се интегрише тако што се експонент увећа за 1, и потом се подели с новим експонентом. За растезање еластичне опруге (учвршћене на другом крају) потребна је сила F = ks промењљивог износа и у смеру растезања, где је k константа опруге, док је s продужење (потенцијал s на прву), тј. пут што га је прешло хватиште силе од нерастегнутог положаја s = 0. Да би растегнула опругу за износ A, сила ће извршити рад:

$W=\int _{0}^{A}ks\,\mathrm {d} s=k\int _{0}^{A}s\,\mathrm {d} s=k\left[{\frac {s^{2}}{2}}\right]_{0}^{A}={\frac {kA^{2}}{2}}$

На знаку интеграла (стилизовани растегнути знак суме, најављује сабирање „бесконачно много бесконачно малих сабирака”) доња и горња граница означавају почетну и завршну тачку пута. Следи износ силе ks (косинуса нема, јер је једнак 1), што се зове подинтегрална функција. Интеграл се завршава диференцијалом пута ds (који се може сматрати „бесконачно малим комадићем пута”). (Стандардна математичка анализа сматра овакав „техничарски” опис некоректиним, али новији радови показују да се може ригорозно оправдати.) У наредном кораку „вади” се испред интеграла константа која множи остатак подинтегралне функције, а потом се s¹ интегрише у s²/2. У задњем кораку уврсте се, уместо s, границе интегрисања: најпре горња граница A, од чега се одузме исти израз са увршеном доњом границом (овде 0, те се не пише).

Опис рада скаларним продуктом

Скаларним множењем два вектора добија се скалар који је једнак умношку њихових износа и косинуса угла међу њима. Ако је сила ^{$\scriptstyle {\vec {F}}$} konstantnog iznosa i smjera, a smjer pravocrtnog gibanja njezinog hvatišta zatvara stalni kut α sa smjerom sile, rad se može zapisati na dva načina:

$W=Fs\cos \alpha ={\vec {F}}\cdot {\vec {d}}$

Drugi izraz označava skalarni produkt vektora sile i vektora pomaka ^{$\scriptstyle {\vec {d}}$} (engleski naziv množenja dot product potječe od točke koja se piše među vektorima). Pomak je usmjerena dužina koja "ide" od početne do završne točke puta na putanji hvatišta sile (opisuje koliko se i u kojemu smjeru ta točka "pomakla"). Jednakost navedenih izraza je očigledna iz definicije skalarnog produkta, budući da je u opisanom slučaju iznos pomaka jednak putu s. No, može se dokazati da formula sa skalarnim produktom sile i pomaka vrijedi i za proizvoljni oblik putanje, uz uvjet da sila ne mijenja iznos i smjer.

Za proizvoljni oblik putanje hvatišta, potrebno je najprije matematički opisati krivulju duž koje se ta točka giba. Gibanje točke u cjelosti je opisano ako za svaki trenutak znademo njezine koordinate, npr. x(t), y(t) i z(t) u pravokutnom Kartezijevom sistemu gdje ih možemo smatrati skalarnim komponentama vektora položaja (radij-vektora) $\scriptstyle {\vec {r}}(t)$ te točke. Vektor položaja je usmjerena dužina kojoj je početak u ishodištu sistema a kraj (strelica) "prati" točku po putanji. Koordinate i vektor položaja često se pišu bez eksplicitne oznake ovisnosti o vremenu, jer se ona kod gibanja točke i tako podrazumijeva.

Kod takvog opisa gibanja, prikladnije je za vektor pomaka iz neke točke 1 u točku 2 koristiti oznaku $\scriptstyle \Delta {\vec {r}}$ (ako znamo da $\scriptstyle \Delta$ označava razliku odnosno promjenu) jer ona eksplicitno pokazuje da se pomak dobija oduzimanjem pripadnih vektora položaja: $\scriptstyle \Delta {\vec {r}}={\vec {r}}_{2}-{\vec {r}}_{1}$, tj. da pomak možemo promatrati kao "promjenu položaja". Duljina putanje (pređeni put s) na krivulji može biti znatno veća od iznosa vektora pomaka $\scriptstyle |\Delta {\vec {r}}|$. No, ako se promatraju sve manji pomaci (vremenski interval $\scriptstyle \Delta t$ između promatranih položaja "teži" prema nuli; na skici je ilustriran početak graničnog procesa) iznosi puta i pomaka postaju sve više jednaki. Jednakost graničnih vrijednosti možemo zapisati pomoću diferencijala: $\scriptstyle |\mathrm {d} {\vec {r}}|=\mathrm {d} s$. Stoga se integral iz opće definicije za rad proizvoljne sile na proizvoljnom putu može kraće zapisati pomoću skalarnog produkta:

$W=\int _{A}^{B}{\vec {F}}\cdot \mathrm {d} {\vec {r}}$

Uzimajući u obzir da je brzina $\scriptstyle {\vec {v}}$ neke točke derivacija njezinog vektora položaja po vremenu (pa je $\scriptstyle \mathrm {d} {\vec {r}}={\vec {v}}\mathrm {d} t$), može se taj integral prevesti u integral po vremenu:

$W=\int _{A}^{B}{\vec {F}}\cdot {\vec {v}}\,\mathrm {d} t$

Podintegralna funkcija $\scriptstyle {\vec {F}}\cdot {\vec {v}}$ je snaga sile. Budući da se snaga definira kao derivacija rada po vremenu, jasno je da rad mora biti jednak integralu snage po vremenu.

Литература

• Jammer, Max (1957). Concepts of Force. Dover Publications, Inc. ISBN 978-0-486-40689-3. 
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th изд.). Brooks/Cole. ISBN 0-534-40842-7. 
• Tipler, Paul (1991). Physics for Scientists and Engineers: Mechanics (3rd ed., extended version изд.). W. H. Freeman. ISBN 0-87901-432-6. 

Спољашње везе

• Work–energy principle