Минимализација кола
У Буловој алгебри, минимализација кола (среће се и израз „минимизација“) је проблем добијања најмањег логичког кола (Булова конфигурација) које представља дату булову функцију или таблицу истинитости. Општи проблем минимализације кола је рачунски тежак, али постоје ефикасне хеуристике као што су Карноове карте и Квајн–Макласкијев алгоритам које олакшавају процес.
Сврха[уреди | уреди извор]
Проблем са компликованим колом (тј. колом са много елемената , као сто су логичка врата која представљају електронски склоп који слижи за остварење логичке операције) састоји се у томе да заузима физички простор за његово спровођење и што се потроши време и новац за његову производњу. Мимимизација кола може бити један облик логичке оптимизације, који се користи да би се смањило подручје комплексне логике у интегрисаним колима.
Пример[уреди | уреди извор]
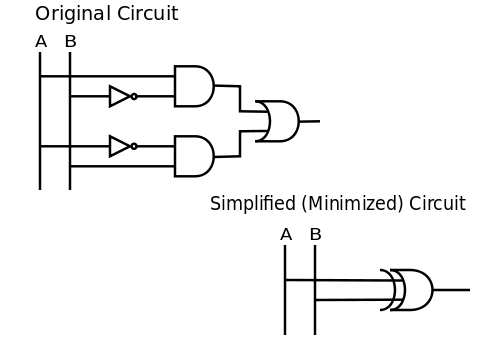
Иако постоји много начина да се минимализује (смањи) коло, ово је пример који минимализује (или поједностављује) булову функцију. Треба имати на уму да је Булова функција, изведна помоћу кола, у директној вези са алгебарским изразом из којег се реализује функција. Размотримо коло које се користи да представи . Евидентно је да су у овом колу употребљене две негације , две конјункције и дисјункција. То значи да су за изградњу кола потребно два инвертора , двоје И врата и ИЛИ врата.
Коло се може поједноставити применом логичких идентитета или помоћу интуиције. Пошто се у примеру наводи да је А тачно када је Б нетачно или обрнуто, може се закључити да ово једноставно значи . У изразима логичких врата, неједнакост једноставно значи ЕКСИЛИ врата (ексклузивно ИЛИ). Према Томе, . Тада су два кола, приказана испод, еквивалентна:
Исправност резултата може се додатно проверити помоћу таблице истинитости.
Литература[уреди | уреди извор]
- De Micheli, Giovanni. Synthesis and Optimization of Digital Circuits. McGraw-Hill, 1994, Part III, Logic-Level Syntesis and Optimization
- Zvi Kohavi, Niraj K. Jha (2009). Switching and Finite Automata Theory (3rd изд.). Cambridge University Press. ISBN 978-0-521-85748-2.
- Knuth, Donald E. (2010). „chapter 7.1.2: Boolean Evaluation”. The Art of Computer Programming. 4A. Addison-Wesley. стр. 96—133. ISBN 978-0-201-03804-0.