Нелинеарна регресија

У статистици, нелинеарна регресија је форма регресионе анализе у којој се експериментални подаци моделују функцијом која је нелинеарна комбинација параметара модела, и зависи од једне или више независних променљивих. Подаци су обрађени методом сукцесивних апроксимација.

Модел[уреди | уреди извор]

Подаци се састоје од независних променљивих које не садрже грешке (експланаторне променљиве), x, и с њима повезаних експерименталних зависних променљивих (респонсне променљиве), y. Свака вредност y се моделује као рандомна променљива са просеком датим у облику нелинеарне функције ф(x,β). Систематске грешке могу да буду присутне, али је њихов третман изван опсега регресионе анализе. Ако независне променљиве садрже грешке, могу се користити модели грешки у променљивама, који су такође изван опсега овог чланка.

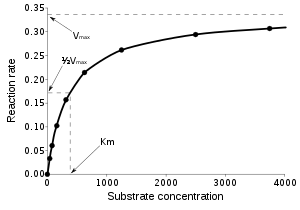
На пример, Михаелис-Ментенов модел ензимске кинетике

v={\frac {V_{\max }\ [{\mbox{S}}]}{K_{m}+[{\mbox{S}}]}}

се може написати као

f(x,{\boldsymbol {\beta }})={\frac {\beta _{1}x}{\beta _{2}+x}}

где је $\beta _{1}$ параметер $V_{\max }$ , $\beta _{2}$ је параметер $K_{m}$ и [С] је независна променљива, x. Функција је нелинеарна, јер се не може изразити као линеарна комбинација две $\beta$ вредности.

Други примери нелинеарних функција су експоненцијалне функције, логаритамске функције, тригонометријске функције, функције степена, Гаусове функције, и Лоренцове криве. Неке функције, као што су експоненцијалне или логаритамске функције, могу се трансформисати тако да поприме линеарни облик. На тако трансформисаним функцијама се може уз опрез применити стандардна линеарна регресија. Погледајте испод одељак о линеаризацији за додатне детаље.

У општем случају, не постоји ираз затворене форме за евалуацију параметара, као што је то случај код линеарне регресије. Обично се користе нумерички оптимизациони алгоритми за одређивање најподеснијих параметара. За разлику од линеарне регресије, могу да постоје многобројни лоцални минимуми оптимизоване функције, а исто тако је могуће да глобални минимум производи бајасну процену. У пракси, се у покушајима налажења глобалног минимума суме квадрата користе процењене вредности параметерара, у спрези са оптимизационим алгоритмима.

Додатни детаљи о нелинеарном моделовању података су доступни у чланцима о најмањим квадратима и нелинеарним најмањим квадратима.

Регресиона статистика[уреди | уреди извор]

Претпоставка у основи овог поступка је да се модел може апроксимирати линеарном функцијом.

f(x_{i},{\boldsymbol {\beta }})\approx f^{0}+\sum _{j}J_{ij}\beta _{j}

где је $J_{ij}={\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}$ . Из овог следи да су естиматори најмањих квадрата дати са

{\hat {\boldsymbol {\beta }}}\approx \mathbf {(J^{T}J)^{-1}J^{T}y} .

Статистички параметри нелинеарне регресија се израчунавају и користе попут њихових линеарно регресионих пандана, али користећи Ј уместо X у формулама. Линеарна апроксимација уноси бајас у статистичке параметре. Због тога је више опреза потребно него при тумачењу статистичких параметара изведених из нелинеараног модела.

Обични и пондерисани најмањи квадрати[уреди | уреди извор]

Обично се подразумева да је најбоља апроксимација кривом да се минимизује сума квадратних остатака. То је приступ (обичних) најмањих квадрата (ОЛС). Међутим, у случајевима где зависна променљива нема константну варијансу, минимизује се сума пондерисаних квадратних остатака; погледајте пондерисане најмање квадрате. Сваки пондер би идеално требало да буде једнак реципрочној вредности варијансе обзервација, мада пондери могу да буду изведени користечи алгоритам итеративно пондерисаних најмањих квадрата.

Линеаризација[уреди | уреди извор]

Трансформација[уреди | уреди извор]

Поједини проблеми нелинеарне регресије се могу пренети у линеарни домен путем подесне трансформације формулације модела.

На пример, размотримо следећи нелинеарно регресиони проблем

y=ae^{bx}U\,\!

са параметерима а и б, и са чланом мултипликативне грешке У. Ако се логаритмују обе стране, добија се

\ln {(y)}=\ln {(a)}+bx+u,\,\!

где је у = лн(У). Из овог следи да је могуће проценити непознате параметере помоћу линеарне регресије лн(y) на x, што је прорачун за који није неопходно користити итеративну оптимизацију. Међутим, нелинеарне трансформације се морају користити уз опрез. Утицај експерименталних вредности ће бити измењен, као и структура грешака модела и интерпретација инференцијалних резултата. Ти ефекти нису увек пожењни. С друге стране, у зависности од тога шта је највећи извор грешака, нелинеарна трансформација може да дистрибуира грешке у нормалном маниру, тако да одлука да се примени нелинеарна трансформацима мора бити базирана разматрању модела.

За Михаелис–Ментенову кинетику, линеарна Лајнвивер–Бурков дијаграм

{\frac {1}{v}}={\frac {1}{V_{\max }}}+{\frac {K_{m}}{V_{\max }[S]}}

за 1/в вс 1/[С] је у широкој употреби. Међутим његова употреба је непожељна, јер је веома сензитиван на грешке у подацима и има јак бајас ка апроксимацији података у специфичном опсегу независне променљиве, [С].

За дистрибуције грешака који припадају експоненцијалној фамилији може се користити линк функција за трансформацију параметара у оквиру генерализовног линеарног модела.

Сегментација[уреди | уреди извор]

Независна или експланаторна променљива (рецимо X) може се поделити у класе или сегменте и линеарна регресија се може применити на сегменте. Сегментирана регресија са анализом интервала поверења може да укаже на чињеницу да се зависна или респонсна променљива (рецимо Y) различито понаша на различитим сегментима.^[1]

Слика показује да салинитет земљишта (X) иницијално нема утицаја на принос усева (Y) семфа (репичиног уља), док кад се пређе критични праг (преломна тачка) салинитет има негативан утицај на принос.^[2]

Види још[уреди | уреди извор]

Референце[уреди | уреди извор]

^ Р.Ј.Оостербаан, 1994, Фреqуенцy анд Регрессион Аналyсис. Ин: Х.П.Ритзема (ед.), Драинаге Принциплес анд Апплицатионс, Публ. 16, пп. 175-224, Интернатионал Институте фор Ланд Рецламатион анд Импровемент (ИЛРИ), Wагенинген, Тхе Нетхерландс. ISBN 978-90-70754-33-4 . Download as PDF : [1]
^ R.J.Oosterbaan, 2002. Drainage research in farmers' fields: analysis of data. Part of project “Liquid Gold” of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Download as PDF : [2]. The figure was made with the SegReg program, which can be downloaded freely from [3]

Literatura[уреди | уреди извор]

Bethea, R. M.; Duran, B. S.; Boullion, T. L. (1985). Statistical Methods for Engineers and Scientists. New York: Marcel Dekker. ISBN 978-0-8247-7227-7.
Meade, N.; Islam, T. (1995). „Prediction Intervals for Growth Curve Forecasts”. Journal of Forecasting. 14 (5): 413—430. doi:10.1002/for.3980140502.
Schittkowski, K. (2002). Data Fitting in Dynamical Systems. Boston: Kluwer. ISBN 978-1-4020-1079-8.
Seber, G. A. F.; Wild, C. J. (1989). Nonlinear Regression. New York: John Wiley and Sons. ISBN 978-0-471-61760-0.

[1] Р.Ј.Оостербаан, 1994, Фреqуенцy анд Регрессион Аналyсис. Ин: Х.П.Ритзема (ед.), Драинаге Принциплес анд Апплицатионс, Публ. 16, пп. 175-224, Интернатионал Институте фор Ланд Рецламатион анд Импровемент (ИЛРИ), Wагенинген, Тхе Нетхерландс. ISBN 978-90-70754-33-4 . Download as PDF : [1]

[2] R.J.Oosterbaan, 2002. Drainage research in farmers' fields: analysis of data. Part of project “Liquid Gold” of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Download as PDF : [2]. The figure was made with the SegReg program, which can be downloaded freely from [3]

[1]

[2]