Nejednakost trougla

Nejednakost trougla jedna je od najvažnijih matematičkih nejednakosti. Originalno, vezivana je za geometriju, konkretno činjenicu da je u trouglu zbir dužina dveju proizvoljnih stranica uvek veća od dužine preostale. Kasnije, ova ideja se proširila i na druge matematičke prostore, prvenstveno na skup realnih i skup kompleksnih brojeva i ostale vektorske prostore kao osobina norme, a potom je dobila i svoje uopštenje na svim metričkim prostorima.

Nejednakost trougla u Euklidskoj geometriji

Zbir dužina dveju stranica je uvek veći od dužine treće.

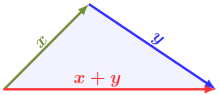
Još je Euklid pokazao da su, u proizvoljnom trouglu, dve stranice, nadograđene jedna na drugu, veće dužine od treće. To je i objavio u prvoj knjizi svojih „Elemenata”, i to kao propoziciju 20. Matematički zapisano, ako su $a$, $b$ i $c$ dužine triju različitih stranica trougla, tada važi

$a+b>c\land b+c>a\land c+a>b$.

Jasno, zbir dužina dveju stranica nikad ne može biti jednak dužini treće, jer u tom slučaju opaženi trougao i ne postoji, tj. u pitanju je samo duž — ovo, između ostalog, pokazuje da je najkraće rastojanje dveju tačaka upravo duž koja ih povezuje. Takođe, nikada ne može biti ni manja, što proističe iz osobina metrika, jer se rastojanje u Euklidskom prostoru može posmatrati kao svojevrsna metrika.

Nejednakost trougla se u slučaju Euklidskih prostora može matematičkom indukcijom proširiti i na proizvoljnu poligonsku (izlomljenu) liniju. U ovom obliku, ona kazuje da je dužina najkraćeg puta između krajnjih temena proizvoljne poligonske linije manja ili jednaka od zbira dužina puteva među svakih dveju susednih temena, tj.

$d(x_{1},x_{n})\leq \sum _{i=1}^{n-1}d(x_{i},x_{i+1})$, gde su $(x_{i})_{i=1}^{n}$ temena poligonske linije, a $d$ standardno Euklidsko rastojanje.

Konačna posledica ovoga je da je u proizvoljnom poligonu svaka stranica kraća od zbira dužina svih ostalih.

Nejednakost trougla kod vektorskih normi

Nejednakost trougla za vektore. Često se inenzitet vektora posmatra kao njegova dužina.

Norma je funkcija $||\bullet ||:V\to K$ definisana nad vektorskim prostorom $V$, kojom se meri intenzitet vektora u polju skalara $K$. Da bi neka funkcija bila norma, mora, pored ostalih, zadovoljiti i uslov nejednakosti trougla, koji glasi

$||a+b||\leq ||a||+||b||$, gde su $a$ i $b$ vektori vektorskog prostora $V$,

tj. intenzitet zbira vektora nije veći od zbira intenziteta tih vektora. Ovo se može proširiti matematičkom indukcijom na proizvoljan broj vektora, tako da glasi

$||\sum _{i=1}^{n}x_{i}||\leq \sum _{i=1}^{n}||x_{i}||$, gde su $(x_{i})_{i=1}^{n}$ vektori.

Nejednakost trougla na skupu kompleksnih i realnih brojeva

Nejednakost trougla najpoznatija je po svojoj primeni na skupu realnih brojeva, gde se koristi u obliku zakonitosti koja se odnosi na apsolutnu vrednost zbira brojeva. Ovde ona glasi

$|a+b|\leq |a|+|b|$.

Ova nejednakost veoma podseća na onu sa vektorskim normama. To nije slučajno, jer se prostor $\mathbb {R}$ može shvatiti kao vektorski prostor nad samim sobom, a apsolutna vrednost je u tom slučaju norma.

Ova nejednakost se, međutim, može uvideti i na drugi način — preko skupa kompleksnih brojeva. Oni se, naime, definišu kao poseban vektorski prostor nad poljem $\mathbb {R}$, i predstavljaju pandan polju $\mathbb {R} ^{2}$, sa nešto drugačijom definicijom operacije množenja, ali se smatraju i poljem. Nad ovim poljem uvodi se operacija modulovanja, i to kao

$|z|={\sqrt {(Rez)^{2}+(Imz)^{2}}}$, za $z$ proizvoljan kompleksan broj.

Ovo umnogome podseća na definiciju Euklidskog rastojanja, kod uvođenja koordinatnog sistema. I kod operacije modula važi nejednakost trougla, tj.

$|z+w|\leq |z|+|w|$, za $z$ i $w$ kompleksne brojeve.

S obzirom da je skup kompleksnih nadskup skupa realnih brojeva, iz definicije modula i apsolutne vrednosti se lako vidi da nejednakost trougla kod realnih brojeva proističe iz nejednakosti za kompleksne. Uzrok ovome je činjenica da realni brojevi zapravo kompleksni kod kojih je imaginarni deo broja jednak nuli.

Nejednakost trougla kod opštih metričkih prostora

Nejednakost trougla u slučaju metričkih prostora — razdaljina dveju tačaka nije veća od zbira njihovih razdaljina do proizvoljne treće tačke.

U metričkom prostoru $(M,d)$, da bi preslikavanje $d$ bilo metrika, mora da ispunjava, između ostalih, uslov nejednakosti trougla koji u ovom slučaju glasi

$d(x,y)\leq d(x,z)+d(z,y)$, gde su $x$, $y$ i $z$ proizvoljni elementi skupa $M$.

Obratna nejednakost trougla

Originalni stav nejednakosti trougla kazuje da je dužina svake stranice veća od razlike dužina ostalih dveju. U geometrijskom slislu ovo znači da za $a$, $b$ i $c$ dužine triju stranica trougla važi

$|a-b|<c$.

U slučaju norme kod vektorskih prostora to, za $a$ i $b$ proizvoljne vektore, glasi

${\bigg |}||a||-||b||{\bigg |}\leq ||a-b||$,

odnosno, za moduo kompleksnih brojeva, pa i apsolutnu vrednost realnih, ovo, za i kompleksne (ili realne) brojeve, izgleda

${\bigg |}|a|-|b|{\bigg |}\leq |a-b|$.

Kod metričkih prostora, ovo, pak, izgleda kao

$|d(x,z)-d(y,z)|\leq d(x,y)$.

Vidi još

• Metrički prostor
• Vektorski prostor
• Euklidska geometrija
• Kompleksni brojevi