Bipartitne dimenzije

U matematičkim oblastima teorije grafova i kombinatorne optimizacije, bipartitna dimenzija ili biklikni pokrivač broja grafa G = (V, E) je minimalan broj biklika (to je kompletni bipartitni podgraf), koji bi trebalo da pokrije sve grane u E. Kolekcija bikliknih pokrivača koji pokrivaju sve grane u G se zove biklikni pokrivač grana, ili ponekad biklikni pokrivač. Bipartitna dimenzija u G je često označena simbolom d(G).

Primer

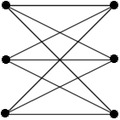
Primeri bikliknog pokrivača grana su dati u sledećim dijagramima:

• Primer za bikliknu pokrivenost grana
• 
  Bipartitni graf...
• 
  ...i pokrivenost sa četiri biklika
• 
  crveni biklik pokrivenosti
• 
  plavi biklik pokrivenosti
• 
  zeleni biklik pokrivenosti
• 
  crni biklik pokrivenosti

Formule za bipartitne dimenzije za neki graf

Biklikna dimenzije za kompletan graf od n čvorova $K_{n}$ је $\lceil \log _{2}n\rceil$. Bipartitna dimenzija krunskog grafa sa 2n čvora jednak je $\sigma (n)$ gde je

$\sigma (n)=\min \left\{\,k\mid n\leq {\binom {k}{\lfloor k/2\rfloor }}\,\right\}$

inverzna funkcija centralnog binomnog koeficijenta (de Caen, Gregory & Pullman 1981). Fišburn i Hamer (Fishburn & Hammer 1996) su definisali bipartitnu dimenziju za neke posebne grafove. Na primer, put $P_{n}$ ima $d(P_{n})=\lfloor n/2\rfloor$ i ciklus $C_{n}$ ima $d(C_{n})=\lceil n/2\rceil$.

Izračunavanje bipartitne dimenzije

Zadatak izračunavanja bipartitne dimenzije za dati graf G je problem optimizacije. Problem rešavanja bipartitne dimenzije može se formulisati kao:

PRIMER: graf $G=(V,E)$ i pozitivan ceo broj $k$.
PITANJE: Da li G zaista ima biklikni prekrivač grana koji sadrži najviše $k$ biklika?

Ovaj problem se javlja kao problem GT18 u knjizi Gerija i Džonsona o NP-kompletnosti, i dosta je direktna reformulacija drugog problema rešavanja porodice ograničenog skupa.

Bazni problem se pojavljuje kao problem SP7 u knjizi Gerija i Džonsona. Ovde, za porodicu ${\mathcal {S}}=\{S_{1},\ldots ,S_{n}\}$ podskupova ograničenog skupa ${\mathcal {U}}$, osnovni skup za ${\mathcal {S}}$ je još jedna porodica podskupova ${\mathcal {B}}=\{B_{1},\ldots ,B_{\ell }\}$ od ${\mathcal {U}}$ tako da svaki skup $S_{i}$ kao unija nekih osnovnih elemenata iz ${\mathcal {B}}$. Skup osnovnog problema se sada prikazuje ovako:

PRIMER: Ograničeni skup ${\mathcal {U}}$, porodica ${\mathcal {S}}=\{S_{1},\ldots ,S_{n}\}$ podskupova ${\mathcal {U}}$ i pozitivan ceo broj k.
PITANJE: Da li postoji osnovni skup ne veći od $k$ za ${\mathcal {S}}$?

Ovaj problem je dokazan da je NP-kompletan od strane Orlina (Orlin 1977), čak i za bipartitne grafove. Stokmejer (Stockmeyer 1975) je ranije dokazao da je NP-kompletnost formula osnovnog baznog problema. Problem ostaje NP-težak, čak i ako ograničimo našu pažnju na bipartitne grafove čija je bipartitna dimenzija zagarantovana da bude najviše $O(\log \,\!n)$, gde n označava veličinu datog problema (Gottlieb, Savage & Yerukhimovich 2005). Sa pozitivne strane, problem je rešiv u polinomijalnom vremenu na bipartitnom domino-slobodnim grafovima (Amilhastre, Janssen & Vilarem 1997).

Što se tiče postojanja približnih algoritama, Simon (Simon 1990) je dokazao da problem ne može biti lepo objašnjen (ako se pretpostavi da je '''P''' ≠ '''NP'''). Zaista, bipartitnu dimenziju je NP-težak približio unutar $|V|^{1/3-\epsilon }$ za svako ustaljeno $\epsilon >0$, već za bipartitne grafove (Gruber & Holzer 2007).

U suprotnosti sa time, dokazuje da je problem prilagodljiv ustaljenim parametrima je vežba dizajniranja jezgrovitih algoritama, kako se pojavljuje u udžbeniku Daunija i Felousa (Downey & Fellows 1999). Flajšner, Mudžuni i Zajder (Fleischner, Mujuni & Szeider 2009) takođe su obezbedili konkretnu granicu veličine rezultujećeg jezgra, što je u međuvremenu unapredio Nor et al (Nor et al. 2010). Zapravo, za dati bipartitni graf sa n čvorova, može se na vreme zaključiti da je $O(f(k))+n^{3}$ sa $f(k)=2^{k2^{k-1}+3k}$ nebitno da li je njegova bipartitna dimenzija najviše k (Nor et al. 2010).

Aplikacije

Problem određivanja bipartitne dimenzije grafa se pojavljuje u raznim kontekstima računarstva. Na primer, u računarskim sistemima, različitim korisnicima sistema može biti dozvoljen ili odbijen pristup raznim resursima. U sistemu za kontrilu pristupa] zasnovanog na ulozi, uloga snabdeva pravo pristupa skupu resursa. Korisnik može da poseduje višestruke uloge i ima dozvolu da pristupi svim resursima koje mu odobravaju neke od njegovih uloga. Takođe, uloga može biti u vlasništvu više korisnika. Problem sa ulogama jeste naći minimalni skup resursa, tako da sve uloge svih korisnika pružaju pristup svim naznačenim resursima. Skup korisnika zajedno sa skupom resursa u sistemu prirodne indukcije bipartitni graf, čije grane predstavljaju dozvole. Svaki biklik u svom grafu je potencijalna uloga, a optimalno rešenje glavnog problema je upravo minimalni biklik pokrivača grana (Ene et al. 2008).

Slični scenario se može naći i u kompjuterskoj bezbednosti, tačnije u emitovanju. U tom slučaju, više poruka mora biti pojedinačno poslato kompletu prijemnika, preko neproverenog kanala. Svaka poruka mora da bude kodirana korišćenjem nekog kriptografskog ključa poznatog samo onim prijemnicima kojima su namenjene. Svaki prijemnik može imati više ključeva za šifrovanje, a svaki ključ će biti raspodeljen između više prijemnika. Problem optimalnog ključa jeste pronaći minimalni skup ključeva za šifrovanje za obezbeđivanje sigurnog prenosa. Kao što je gore navedeno, problem se može podesiti pomoću bipartitnog grafa čiji se minimalni broj bikliknih prekrivača grana podudara sa reševanjem za optimalni problem pronalaženja ključa (Shu, Lee & Yannakakis 2006).

Drugačija aplikacija može se naći u biologiji, gde se minimalni broj bikliknih pokrivenosti grana koristi u matematičkim obrascima leukocitnog antigena kod ljudi (HLA) (Nau et al. 1978).

Literatura

• Amilhastre, Jérôme; Janssen, Philippe; Vilarem, Marie-Catherine (1997), „Computing a minimum biclique cover is polynomial for bipartite domino-free graphs”, Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, 5–7 January 1997, New Orleans, Louisiana., ACM/SIAM, стр. 36—42 
• de Caen, Dominique; Gregory, David A.; Pullman, Norman J. (1981), „The Boolean rank of zero-one matrices”, Ур.: Cadogan, Charles C., 3rd Caribbean Conference on Combinatorics and Computing, Department of Mathematics, University of the West Indies, стр. 169—173 .
• Downey, Rod; Fellows, Michael R. (1999), Parameterized complexity, Springer, ISBN 978-0-387-94883-6 .
• Ene, Alina; Horne, William G.; Milosavljevic, Nikola; Rao, Prasad; Schreiber, Robert; Tarjan, Robert Endre (2008), „Fast exact and heuristic methods for role minimization problems”, Ур.: Ray, Indrakshi; Li, Ninghui, 13th ACM Symposium on Access Control Models and Technologies (SACMAT 2008), ACM, стр. 1—10 .
• Fishburn, Peter C.; Hammer, Peter L. (1996), „Bipartite dimensions and bipartite degrees of graphs”, Discrete Mathematics, 160 (1–3): 127—148, doi:10.1016/0012-365X(95)00154-O .
• Fleischner, Herbert; Mujuni, Egbert; Paulusma, Daniël; Szeider, Stefan (2009), „Covering graphs with few complete bipartite subgraphs”, Theoretical Computer Science, 410 (21-23): 2045—2053, doi:10.1016/j.tcs.2008.12.059 .
• Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 978-0-7167-1045-5 .
• Gottlieb, Lee-Ad J.; Savage, John E.; Yerukhimovich, Arkady (2005), „Efficient data storage in large nanoarrays”, Theory of Computing Systems, 38 (4): 503—536, doi:10.1007/s00224-004-1196-9 .
• Gruber, Hermann; Holzer, Markus (2007), „Inapproximability of Nondeterministic State and Transition Complexity Assuming P <> NP.”, Ур.: Harju, Terjo; Karhumäki, Juhani; Lepistö, Arto, 11th International Conference on Developments in Language Theory (DLT 2007), LNCS, 4588, Turku, Finland: Springer, стр. 205—216, doi:10.1007/978-3-540-73208-2_21 .
• Monson, Sylvia D.; Pullman, Norman J.; Rees, Rolf (1995), „A survey of clique and biclique coverings and factorizations of (0,1)-matrices”, Bulletin of the ICA, 14: 17—86 .
• D. S. Nau, D. S.; Markowsky, G.; Woodbury, M. A.; Amos, D. B. (1978), „A mathematical analysis of human leukocyte antigen serology” (PDF), Mathematical Biosciences, 40: 243—270, doi:10.1016/0025-5564(78)90088-3 .
• Nor, Igor; Hermelin, Danny; Charlat, Sylvain; Engelstadter, Jan; Reuter, Max; Duron, Olivier; Sagot, Marie-France (2010). „Mod/Resc Parsimony Inference”. arXiv:1002.1292  [cs.DS]. 
• Orlin, James (1977), „Contentment in graph theory: covering graphs with cliques”, Indagationes Mathematicae, 80 (5): 406—424, doi:10.1016/1385-7258(77)90055-5 .
• Shu, Guoqiang; Lee, David; Yannakakis, Mihalis (2006), „A note on broadcast encryption key management with applications to large scale emergency alert systems.”, 20th International Parallel and Distributed Processing Symposium (IPDPS 2006), IEEE .
• Simon, Hans-Ulrich (1990), „On Approximate Solutions for Combinatorial Optimization Problems”, SIAM Journal on Discrete Mathematics, 3 (2): 294—310, doi:10.1137/0403025 .
• Stockmeyer, Larry J. (1975), The set basis problem is NP-complete, Technical Report RC-5431, IBM .

Spoljašnje veze

• blog entry about bipartite dimension by David Eppstein