Проблем максималног тока

У теорији оптимизације Проблем максималног протока укључује налажење подесног протока кроз једно-изворну једно-завршну транспортну мрежу која је максимална.
Проблем максималног протока се може посматрати као специјални случај комплекснијих проблема транспортних мрежа као што је проблем кружења. Максимална вредност с-т тока(односно тока од извора ка завршном току је једнак минималном капацитету с-т пресека(однсно пресека од с до т) у мрежи, као што је наведено у максимални-проток минимални-пресек теореми. _TOC_
Историја
[уреди | уреди извор]Проблем Максималног тока је први пут формулисан 1954 од стране Т. Е Харрис као поједностављен модел тока совјетске железнице[1]. У 1955. години Лестер Р. Форд. Јр и Делберт Р. Фулкерсон направили су први познати алгоритам Форд-Фулкерсон алгоритам.[2][3]
Током времена откривена су разна побољшана решењаПроблема максималног протока, посебно алгоритам најраће промене пута од Едмондса и Карпа и независно Динитз-а. Алгоритам блокиарања тока од Динитз-а. Алгоритам гуранја-ознаке од Голдберг-а и Тарјан-а. Бинарно блокирање тока Голдберг-а и Рао-а. Алгоритам електричног тока Кристиано, Келнер, Мадри и Спиелман-а налази отприлике оптималан максимални ток , али ради само са неусмереним графовима.
Дефиниција
[уреди | уреди извор]
Нека је Н=(В, Е) мрежа са с, т∈В чворовима који су извор и понор од Н респективно Капацитет чвора је сликанје ц:Е→Р+ где је Цув или Ц(у, в). Представља макцималан проток кроз чвор. Проток је сликање ф:Е'→Р+ где је фу, в или ф(у, в) под утиском ограничења:
1.фув≤цув за свако (у, в)∈В(Ограничење капацитета:проток кроз чвор не може да надмаши његов капацитет)
2.Σу:(у, в)∈Еф(у, в)=Σу:(у, в)∈Ефсв за свако в∈Б\{с, т}(Конзервација протока:сума протока која улази у чвор мора да буде једнака суми протока која излази из чвора , осим извора и понора).
Вредност протока је деФинисана једнакошћу |ф|=Σв:(с, в)∈Ефсв где с је извор од Н. Представља количину протока која пролази од извора до понора.
у Проблему максималног протока треба максимизовати |ф| , тако да постоји што више протока од с до т.
Решења
[уреди | уреди извор]Моземо да дефинишемо резидуални граф која даје систематични начин за тражење унапред-уназад операције. да би могао да се нађе максимални проток.
Са задатом транспортном мрежом Г , и протоком ф у г , можемо да деФинишемо резидуални граф Гф од Г са респектом по ф као што следи:
1. Скуп чворова од Гф је исти као и Г.
2. Сваки чвор е=(у, в) од Гф је са капацитетом од Це-Ф(е).
3. Сваки чвор е'=(в, у) Гф је са капацитетом од ф(е).
Следећа табела приказује алгоритме за решавање проблема максималног протока.
| Метода | Комплексност | Опис |
| Линеарно програмирање | Ограничења су задата са дефиницијом легалног протока. | |
| форд-фулкерсон алгоритам | О(макс ф) | Све док постоји путања кроз Резидуални граф, послати минимум преосталих капацитета кроз путању. Алгоритам ради цамо ако су све тежине цели бројеви. Иначе је могуће да форд-фулкерсонов алгоритам неће конвергирати ка максималној вредности. |
| Едмондс-Карп алгоритам | О(ВЕ2) | Специјализација форд-фулкерсон алгоритма , налажење увеличавајуће путање са претрагом графа у ширину. |
| Динитцово блокирање протока алгоритма | О(В2Е) | У свакој Фази алгоритма гради се слојевит граф са претрагом у ширину у резидуалном графу. Максимални проток у слојевитом графу може бити израчунат у О(ВЕ) времену, а максимални број Фаза је н-1. У мрежама са јединичхим капацитетима , Динитцов алгоритам се завршава у О(Екорен(В)) |
| Генерални пуш-релабел алгоритам максималног протока | О(В2Е) | Пуш-релабел алгоритам одржава предток такође ток функције са могућношћу вишка у чворовима. Алгоритам се извршава док постоји чвор са вишком такође активним чвором у графу. Пуш операција повећава проток на резидуалним гранама , а висина на контролама графа чије се резидуалне гране могу "гурнути“. Висина функције је промењена са релабел операцијом. Коректна дефиниција ових операција гарантује да је резултујући проток функције је максимални проток |
| Пуш-релабел алгоритам са фИфО правилом селекције чвора | О(В3) | пуш-релабел алгоритам варијанта која увек бира најскорије коришћен активни чвор и изводи пуш операције док остатак није позитиван или док не постоји прихватљив остатак грана од овог чвора |
| Динитцово блокирање протока алгоритма са динамичким дрветом | О(ВЕлог(В)) | Струстура података динамичког дрвећа убрзава израчунавање максималног протока у слојевитом графу до О(Е лог(Б)) |
| Пуш-релабел алгоритам са динамичким дрветом | О(БЕлог(Б2/Е)) | Алгоритам гради дрвећа ограничехе величине на резидуалном графу с обзиром на висину функције. Ова дрвећа дају више-нивоа пуш операције |
| Бинарно блокирање протока са динамичким дрветом | О(Емин(В2/3/sup>, корен(Е))лог(В2/Е)лог У) | Вредност У одговара максимуму капацитета мреже. |
| МПМ(Малхотра, Прамодх-Кумар и Махесхвари) Алгоритам | О(Б3) | |
| Џим Орлинов + КРТ(Кинг, Рао, Тарјан) Алгоритам | О(ВЕ) | Орлинов алгоритам решава проблем максималног протока у О(ВЕ) времену за м≤О(х(16/15)-е) док га КРТ решава у О(ВЕ) за м>н1+е |
Теорема интегралног тока
[уреди | уреди извор]По теореми интегралног тока:
Ако сваки чвор у трансортној мрежи има интегрални капацитет , онда постоји интегрални максимум протока.
Употреба
[уреди | уреди извор]
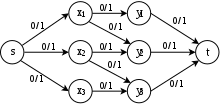
Више-изворни више-понорни проблем максималног протока
са задатом мрежом Н=(В, Е) са скупом извора С={с1, ..., сн} и скуп понора Т = {т1, ..., тн} уместо само једног извора и понора Треба да нађемо максимални проток преко н. Можемо да трансформишемо више-изворни, више-понорни проблем у проблем максималног протока додавањем интегрисаног извора који се повезује за сваки чвор у С и интегрисани понор за који су сви чворови из Т повезани(Такође познати као супер-извор и супер-понор)Са бесконачним капацитетом на свакој грани(видети фигуру 4.1.1).
Покривач минималне путање у директном ацикличном графу
Са задатим графом Г=(В, Е) треба да нађемо минимални број путања да покријемо сваки чвор у В. Можемо да конструишемо бипартитивни граф Г=(Визлазно∪Вулазно, Е) од Г где:
1. Визлазно={в∈В: в има позитиван излазни степен}.
2. Вулазно={в∈В: в има позитиван улазни степен}.
3. Е = {(у, в)∈(Визлазно, Вулазно): (у, в)∈Е}.
Онда може бити приказано преко Конигове теореме Г има усаглашену величину од м само ако постоји н-м путања који покривају сваки чвор у графу Г где је н број чворова у Г. Дакле проблем се може решити налажењем максималног броја упаривања у Г.
Максимална бројност бипартитивног упаривања
Са задатим бипартитивном графом Г=(З∪Џ, Е) Треба да нађемо максимални број повезивања у Г , то је повезивање које садржа максимални могући број грана. Овај проблем се може трасформисати у проблем максималног протока конструисањем мреже N = (З∪Џ∪{с, т}, Е' } где:
1. Е садржи гране у Г усмерене од Џ до З
2.(с, џ)∈Е' за свако џ∈Џ и (з, т)∈Е' за свако з∈З
3.ц(е)=1 за свако е∈Е'
Онда Максимална вредност Протока у Н је једнака величини максималног упаривања у Г.
Проблем Максималног протока са капацитетом чворова
У задатој мрежи Н=(В, Е) где посотји капацитет за сваки чвор , као и за сваку грану постоји пресликавање ц:В→Р+ обележено са ц(в) тако да проток ф мора да испуњава услове ограничења капацитета као и конзервације протока и такође ограничење капацитета чворова.
Σи∈В фив≤ц(в) за свако в∈В\{с, т}
другим речима количина протока која пролази кроз чвор не може да надмашује његов капацитет.
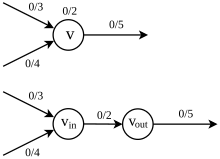
Да би се нашао максимални проток кроз Н Мо+емо да трнсформишемо проблем у првобитни проблем максималног протока тако што ћемо да проширимо Н. Прво сваки в∈В заменимо са вулазно и визлазно , где је вулазно повезано гранама које улазе у в , а визлазно је повезано гранама које излазе из в, онда придодати капацитет ц(в) грани која повезује вулазно и визлазно(видети фигуру 4.4.1 али опазити да су вулазно и визлазно погрешно замењени). У овој проширеној мрежи ограничење капацитета чворава је уклоњено па се проблем може третирати као првобитни проблем максималног протока.
Максимална независна путања
Са задатим усмереним графом Г=(В, Е) и два чвора с и т , треба да нађемо максимални број независних путања од с до т. Две путање су независне ако немају заједнички чвор осим с и т. Можемо да конструишемо мрежу Н=(В, Е) од графа г са капацитетима чворова где:
1.с и т су извор и понор од Н у том редоследу.
2.ц(в)=1 за свако в∈В
3.ц(е)=1 за свако е∈Е
Онда је вредност максималног протока једнака Максималном броју путања од с до т.
Максимална путања дисјунктних грана
Са задатим усмереним графом Г=(В, Е) и два чвора с и т треба да нађемо максимални број путања са дисјунктним гранама од с до т. Овај проблем можемо да трансформишемо у проблем максималног протока конструисањем мреже Н=(В, Е) из Г где су с и т извор и понор (у том редоследу) и свакој грани придружимо јединични капацитет.
Види још
[уреди | уреди извор]Проблеми минималне цене протока
Референце
[уреди | уреди извор]- ^ Александер Сцхријвер,"О Историји транспортације и проблема максималног протока"
- ^ форд Л. Р., ЈР;Фулкерсон Д. Р. "Максимални проток кроз мрежу"
- ^ форд Л. Р., ЈР;фулкерсон Д. Р. "Проток у мрежи"
