Призма (геометријска фигура) — разлика између измена
. |
|||
| Ред 1: | Ред 1: | ||
{{short description|Чврсто тело са паралелним основама повезаним паралелограмима}}{{rut}} |
|||
{{bez_izvora}} |
|||
{{Друго значење2|Призма}} |
{{Друго значење2|Призма}} |
||
{{Infobox polyhedron |
|||
'''Призма''' је геометријски [[полиедар]] ограничен са две паралелне подударне основе (основа може бити било који многоугао) које су повезане паралелограмима (бочним странама). У зависности од многоугла у основи, призма може бити троугаона, четвороугаона, петоугаона итд. |
|||
| name = Set of uniform {{nowrap|{{mvar|n}}-gonal}} prisms |
|||
| image = Hexagonal Prism BC.svg |
|||
| caption = Example uniform hexagonal prism |
|||
| type = [[Uniform polyhedron|uniform]] in the sense of [[Semiregular polyhedron|semiregular]] polyhedron |
|||
| euler = |
|||
| faces = 2 {{nowrap|{{mvar|n}}-gonal}} [[regular polygon]]s<br>{{mvar|n}} [[square]]s |
|||
| edges = {{math|3''n''}} |
|||
| vertices = {{math|2''n''}} |
|||
| vertex_config = {{math|4.4.''n''}} |
|||
| schläfli = {{math|{''n''}×{} }}<ref>[[Norman Johnson (mathematician)|N.W. Johnson]]: ''Geometries and Transformations'', (2018) {{ISBN|978-1-107-10340-5}} Chapter 11: ''Finite symmetry groups'', 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3b</ref><br>{{math|''t''{2, ''n''} }} |
|||
| wythoff = |
|||
| coxeter = {{CDD|node_1|2|node_1|n|node}} |
|||
| conway = {{math|P''n''}} |
|||
| symmetry = {{math|[[Dihedral symmetry in three dimensions|''D''<sub>''n''h</sub>]], [''n'',2], (*''n''22),}} order {{math|4''n''}} |
|||
| rotation_group = {{math|''D''<sub>''n''</sub>, [''n'',2]<sup>+</sup>, (''n''22),}} order {{math|2''n''}} |
|||
| surface_area = |
|||
| volume = |
|||
| dual = [[Convex polytope|convex]] dual-[[Uniform polyhedron|uniform]] {{nowrap|{{mvar|n}}-gonal}} [[bipyramid]] |
|||
| properties = convex, [[regular polygon]] faces, [[vertex-transitive]], translated bases, sides ⊥ bases |
|||
| vertex_figure = |
|||
| net = Generalized prisim net.svg |
|||
}} |
|||
'''Призма''' је геометријски [[полиедар]] ограничен са две паралелне подударне основе (основа може бити било који многоугао) које су повезане паралелограмима (бочним странама). У зависности од многоугла у основи, призма може бити троугаона, четвороугаона, петоугаона итд. All [[Cross section (geometry)|cross-sections]] parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a [[pentagonal]] base is called a pentagonal prism. Prisms are a subclass of [[prismatoid]]s. |
|||
Like many basic geometric terms, the word ''prism'' ({{ety|el|''πρίσμα'' (prisma)|something sawed}}) was first used in [[Euclid's Elements]]. Euclid defined the term in Book XI as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. However, this definition has been criticized for not being specific enough in relation to the nature of the bases, which caused confusion among later geometry writers.<ref name="Malton1774">{{cite book|author=Thomas Malton|title=A Royal Road to Geometry: Or, an Easy and Familiar Introduction to the Mathematics. ... By Thomas Malton. ...|url=https://books.google.com/books?id=-3tLfuCB97AC&pg=PA360|year=1774|publisher=author, and sold|pages=360–}}</ref><ref name="Elliot1845">{{cite book|author=James Elliot|title=Key to the Complete Treatise on Practical Geometry and Mensuration: Containing Full Demonstrations of the Rules ...|url=https://books.google.com/books?id=qilLAAAAYAAJ&pg=PA3|year=1845|publisher=Longman, Brown, Green, and Longmans|pages=3–}}</ref> |
|||
== Right prism, uniform prism == |
|||
=== Right prism === |
|||
A '''right prism''' is a prism in which the joining edges and faces are ''[[perpendicular]]'' to the base faces.<ref name=":0">William F. Kern, James R. Bland, ''Solid Mensuration with proofs'', 1938, p.28</ref> This applies [[iff|if]] all the joining faces are ''[[rectangular]]''. |
|||
The [[Dual polyhedron|dual]] of a ''right'' ''n''-prism is a ''right'' ''n''-[[bipyramid]]. |
|||
A right prism (with rectangular sides) with [[Regular polygon|regular ''n''-gon]] bases has Schläfli symbol { }×{''n''}. It approaches a [[Cylinder (geometry)|cylindrical]] solid as ''n'' approaches [[infinity]]. |
|||
==== Special cases ==== |
|||
*A right rectangular prism (with a rectangular base) is also called a ''[[cuboid]]'', or informally a ''rectangular box''. A right rectangular prism has [[Schläfli symbol]] { }×{ }×{ }. |
|||
*A right square prism (with a square base) is also called a ''square cuboid'', or informally a ''square box''. |
|||
Note: some texts may apply the term ''rectangular prism'' or ''square prism'' to both a right rectangular-based prism and a right square-based prism. |
|||
=== Uniform prism === |
|||
A '''uniform prism''' or '''semiregular prism''' is a ''right prism'' with ''[[Regular polygon|regular]] bases'' and ''[[square]] sides'', since such prisms are in the set of [[uniform polyhedra]]. |
|||
A uniform ''n''-gonal prism has [[Schläfli symbol]] t{2,''n''}. |
|||
Right prisms with regular bases and equal edge lengths form one of the two infinite series of [[semiregular polyhedra]], the other series being [[antiprism]]s. |
|||
{{UniformPrisms}} |
|||
== Подела == |
== Подела == |
||
| Ред 18: | Ред 68: | ||
== Површина призме == |
== Површина призме == |
||
Површина призме је збир површина свих страна призме. Најједноставније је израчунати површину бочних страна -М- призме и саберемо са две основе. |
Површина призме је збир површина свих страна призме. Најједноставније је израчунати површину бочних страна -М- призме и саберемо са две основе. |
||
:<math>2B + Ph</math> |
|||
М = О<sub>b</sub>*H |
|||
where ''B'' is the area of the base, ''h'' the height, and ''P'' the base [[perimeter]]. |
|||
The surface area of a right prism whose base is a regular ''n''-sided [[polygon]] with side length ''s'' and height ''h'' is therefore: |
|||
P = 2*B+M |
|||
:<math>A = \frac{n}{2} s^2 \cot{\left(\frac{\pi}{n}\right)} + n s h</math> |
|||
== Запремина призме == |
== Запремина призме == |
||
Запремину призме израчунавамо тако што површину основе призме помножимо висином призме. |
Запремину призме израчунавамо тако што површину основе призме помножимо висином призме. |
||
:<math>V = Bh</math> |
|||
V=B*H |
|||
where ''B'' is the base area and ''h'' is the height. The volume of a prism whose base is an ''n''-sided [[regular polygon]] with side length ''s'' is therefore: |
|||
:<math>V = \frac{n}{4}hs^2 \cot\left(\frac{\pi}{n}\right)</math> |
|||
== [[Schlegel diagram]]s == |
|||
{| class=wikitable |
|||
|- align=center |
|||
|[[File:Triangular prismatic graph.png|100px]]<BR>P3 |
|||
|[[File:Cubical graph.png|100px]]<BR>P4 |
|||
|[[File:Pentagonal prismatic graph.png|100px]]<BR>P5 |
|||
|[[File:Hexagonal prismatic graph.png|100px]]<BR>P6 |
|||
|[[File:Heptagonal prismatic graph.png|100px]]<BR>P7 |
|||
|[[File:Octagonal prismatic graph.png|100px]]<BR>P8 |
|||
|} |
|||
== Symmetry == |
|||
The [[symmetry group]] of a right ''n''-sided prism with regular base is [[Dihedral group|D<sub>''n''h</sub>]] of order 4''n'', except in the case of a cube, which has the larger symmetry group [[Octahedral symmetry|O<sub>h</sub>]] of order 48, which has three versions of D<sub>4h</sub> as [[subgroup]]s. The [[Point groups in three dimensions#Rotation groups|rotation group]] is D<sub>''n''</sub> of order 2''n'', except in the case of a cube, which has the larger symmetry group O of order 24, which has three versions of D<sub>4</sub> as subgroups. |
|||
The symmetry group D<sub>''n''h</sub> contains [[Point reflection|inversion]] [[If and only if|iff]] ''n'' is even. |
|||
The [[Hosohedron|hosohedra]] and [[Dihedron|dihedra]] also possess dihedral symmetry, and an ''n''-gonal prism can be constructed via the [[Truncation (geometry)|geometrical truncation]] of an ''n''-gonal hosohedron, as well as through the [[cantellation]] or [[Expansion (geometry)|expansion]] of an ''n''-gonal dihedron.<!--do hosohedra work with expansion?--> |
|||
== Truncated prism == |
|||
A '''truncated prism''' is a prism with non-[[Parallel (geometry)|parallel]] top and bottom faces.<ref>William F. Kern, James R. Bland, ''Solid Mensuration with proofs'', 1938, p.81</ref> |
|||
[[File:TruncatedTriangularPrism.png|thumb|left|220px|Example truncated triangular prism. Its top face is truncated at an oblique angle, but it is NOT an [[Prism (geometry)#Oblique prism|oblique prism]]!]] |
|||
== Twisted prism == |
|||
A '''twisted prism''' is a nonconvex polyhedron constructed from a uniform ''n''-prism with each side face bisected on the square diagonal, by twisting the top, usually by {{sfrac|{{pi}}|''n''}} radians ({{sfrac|180|''n''}} degrees) in the same direction, causing sides to be concave.<ref>The facts on file: Geometry handbook, Catherine A. Gorini, 2003, {{isbn|0-8160-4875-4}}, p.172</ref><ref>{{Cite web|url=http://www.korthalsaltes.com/cuadros.php?type=twisted-prisms|title = Pictures of Twisted Prisms}}</ref> |
|||
A twisted prism cannot be [[Dissection (geometry)|dissected]] into tetrahedra without adding new vertices. The smallest case: the triangular form, is called a [[Schönhardt polyhedron]]. |
|||
An ''n''-gonal ''twisted prism'' is topologically identical to the ''n''-gonal uniform [[antiprism]], but has half the [[List_of_spherical_symmetry_groups#Dihedral_symmetry|symmetry group]]: D<sub>''n''</sub>, [''n'',2]<sup>+</sup>, order 2''n''. It can be seen as a nonconvex antiprism, with tetrahedra removed between pairs of triangles. |
|||
{| class=wikitable |
|||
!3-gonal |
|||
!colspan=2|4-gonal |
|||
!12-gonal |
|||
|- align=center |
|||
|[[File:Schönhardt polyhedron.svg|120px]]<BR>[[Schönhardt polyhedron]] |
|||
|[[File:Twisted square antiprism.png|120px]]<BR>Twisted square prism |
|||
|[[File:Square antiprism.png|120px]]<BR>[[Square antiprism]] |
|||
|[[File:Twisted_dodecagonal_antiprism.png|180px]]<BR>Twisted dodecagonal antiprism |
|||
|} |
|||
== Frustum == |
|||
A [[frustum]] is a similar construction to a prism, with [[trapezoid]] lateral faces and differently sized top and bottom polygons. |
|||
[[File:Pentagonal frustum.svg|thumb|220px|Example pentagonal frustum]] |
|||
== Star prism == |
|||
{{See|Prismatic uniform polyhedron}} |
|||
A '''star prism''' is a nonconvex polyhedron constructed by two identical [[star polygon]] faces on the top and bottom, being parallel and offset by a distance and connected by rectangular faces. A ''uniform star prism'' will have [[Schläfli symbol]] {''p''/''q''} × { }, with ''p'' rectangle and 2 {''p''/''q''} faces. It is topologically identical to a ''p''-gonal prism. |
|||
{| class=wikitable |
|||
|+ Examples |
|||
!{ }×{ }<sub>180</sub>×{ } |
|||
!colspan=2|[[Truncation_(geometry)#Generalized_truncations|t<sub>a</sub>]]{3}×{ } |
|||
!{5/2}×{ } |
|||
!{7/2}×{ } |
|||
!{7/3}×{ } |
|||
!{8/3}×{ } |
|||
|- align=center |
|||
|D<sub>2h</sub>, order 8 |
|||
|colspan=2|D<sub>3h</sub>, order 12 |
|||
|D<sub>5h</sub>, order 20 |
|||
|colspan=2|D<sub>7h</sub>, order 28 |
|||
|D<sub>8h</sub>, order 32 |
|||
|- |
|||
|[[File:crossed-square_prism.png|100px]] |
|||
|[[File:Crossed hexagonal prism.png|100px]] |
|||
|[[File:Crossed-unequal hexagonal prism.png|100px]] |
|||
|[[File:Pentagrammic prism.png|100px]] |
|||
|[[File:Heptagrammic prism 7-2.png|100px]] |
|||
|[[File:Heptagrammic prism 7-3.png|100px]] |
|||
|[[File:Prism 8-3.png|100px]] |
|||
|} |
|||
=== Crossed prism === |
|||
A '''crossed prism''' is a nonconvex polyhedron constructed from a prism, where the vertices of one base are [[Point reflection|inverted around the center]] of this base (or rotated by 180°). This transforms the side rectangular faces into [[crossed rectangle]]s. For a regular polygon base, the appearance is an ''n''-gonal [[hour glass]]. All oblique edges pass through a single body center. Note: no vertex is at this body centre. A crossed prism is topologically identical to an ''n''-gonal prism. |
|||
{| class=wikitable |
|||
|+ Examples |
|||
!{ }×{ }<sub>180</sub>×{ }<sub>180</sub> |
|||
!colspan=2|t<sub>a</sub>{3}×{ }<sub>180</sub> |
|||
!{3}×{ }<sub>180</sub> |
|||
!{4}×{ }<sub>180</sub> |
|||
!{5}×{ }<sub>180</sub> |
|||
!{5/2}×{ }<sub>180</sub> |
|||
!{6}×{ }<sub>180</sub> |
|||
|- align=center |
|||
|D<sub>2h</sub>, order 8 |
|||
|colspan=3|D<sub>3d</sub>, order 12 |
|||
|D<sub>4h</sub>, order 16 |
|||
|colspan=2|D<sub>5d</sub>, order 20 |
|||
|D<sub>6d</sub>, order 24 |
|||
|- |
|||
|[[File:crossed_crossed-square_prism.png|100px]] |
|||
|[[File:Crossed crossed-hexagonal prism.png|100px]] |
|||
|[[File:Crossed crossed-unequal hexagonal prism.png|100px]] |
|||
|[[File:Crossed triangular prism.png|100px]] |
|||
|[[File:Crossed cube.png|100px]] |
|||
|[[File:Crossed pentagonal prism.png|100px]] |
|||
|[[File:Crossed pentagrammic prism.png|100px]] |
|||
|[[File:Crossed2 hexagonal prism.png|100px]] |
|||
|} |
|||
=== Toroidal prism === |
|||
A '''toroidal prism''' is a nonconvex polyhedron like a ''crossed prism'', but without bottom and top base faces, and with simple rectangular side faces closing the polyhedron. This can only be done for even-sided base polygons. These are topological tori, with [[Euler characteristic]] of zero. The topological [[polyhedral net]] can be cut from two rows of a [[square tiling]] (with [[vertex configuration]] ''4.4.4.4''): a band of ''n'' squares, each attached to a [[Rectangle|crossed rectangle]]. An ''n''-gonal toroidal prism has 2''n'' vertices, 2''n'' faces: ''n'' squares and ''n'' crossed rectangles, and 4''n'' edges. It is topologically [[Self-dual polyhedron|self-dual]]. |
|||
{| class=wikitable |
|||
|+ Examples |
|||
|- align=center |
|||
|D<sub>4h</sub>, order 16 |
|||
|D<sub>6h</sub>, order 24 |
|||
|- align=center |
|||
|''v''=8, ''e''=16, ''f''=8 |
|||
|''v''=12, ''e''=24, ''f''=12 |
|||
|- |
|||
|[[File:Toroidal_square_prism.png|100px]] |
|||
|[[File:Toroidal hexagonal prism.png|100px]] |
|||
|} |
|||
== Prismatic polytope == |
|||
A ''prismatic [[polytope]]'' is a higher-dimensional generalization of a prism. An ''n''-dimensional prismatic polytope is constructed from two ({{nowrap|''n'' − 1}})-dimensional polytopes, translated into the next dimension. |
|||
The prismatic ''n''-polytope elements are doubled from the ({{nowrap|''n'' − 1}})-polytope elements and then creating new elements from the next lower element. |
|||
Take an ''n''-polytope with ''f<sub>i</sub>'' [[Face|''i''-face]] elements ({{nowrap|''i'' {{=}} 0, ..., ''n''}}). Its ({{nowrap|''n'' + 1}})-polytope prism will have {{nowrap|2''f''<sub>''i''</sub> + ''f''<sub>''i''−1</sub>}} ''i''-face elements. (With {{nowrap|''f''<sub>−1</sub> {{=}} 0}}, {{nowrap|''f''<sub>''n''</sub> {{=}} 1}}.) |
|||
By dimension: |
|||
*Take a [[polygon]] with ''n'' vertices, ''n'' edges. Its prism has 2''n'' vertices, 3''n'' edges, and {{nowrap|2 + ''n''}} faces. |
|||
*Take a [[polyhedron]] with ''v'' vertices, ''e'' edges, and ''f'' faces. Its prism has 2''v'' vertices, {{nowrap|2''e'' + ''v''}} edges, {{nowrap|2''f'' + ''e''}} faces, and {{nowrap|2 + ''f''}} cells. |
|||
*Take a [[polychoron]] with ''v'' vertices, ''e'' edges, ''f'' faces, and ''c'' cells. Its prism has 2''v'' vertices, {{nowrap|2''e'' + ''v''}} edges, {{nowrap|2''f'' + ''e''}} faces, {{nowrap|2''c'' + ''f''}} cells, and {{nowrap|2 + ''c''}} hypercells. |
|||
=== Uniform prismatic polytope === |
|||
A regular ''n''-polytope represented by [[Schläfli symbol]] {{nowrap|{''p'', ''q'', ...,}} ''t''} can form a uniform prismatic ({{nowrap|''n'' + 1}})-polytope represented by a [[Cartesian product]] of [[Schläfli symbol#Prismatic forms|two Schläfli symbols]]: {{nowrap|{''p'', ''q'', ...,}} ''t''}×{}. |
|||
By dimension: |
|||
*A 0-polytopic prism is a [[line segment]], represented by an empty [[Schläfli symbol]] {}. |
|||
**[[Image:Complete graph K2.svg|60px]] |
|||
*A 1-polytopic prism is a [[rectangle]], made from 2 translated line segments. It is represented as the product Schläfli symbol {}×{}. If it is [[square]], symmetry can be reduced: {{nowrap|{}×{} {{=}} {4}.}} |
|||
**[[Image:Square diagonals.svg|60px]]Example: Square, {}×{}, two parallel line segments, connected by two line segment ''sides''. |
|||
*A [[polygon]]al prism is a 3-dimensional prism made from two translated polygons connected by rectangles. A regular polygon {''p''} can construct a uniform ''n''-gonal prism represented by the product {''p''}×{}. If {{nowrap|''p'' {{=}} 4}}, with square sides symmetry it becomes a [[cube]]: {{nowrap|{4}×{} {{=}} {4, 3}.}} |
|||
**[[Image:Pentagonal prism.png|60px]]Example: [[Pentagonal prism]], {5}×{}, two parallel [[pentagon]]s connected by 5 rectangular ''sides''. |
|||
*A [[Polyhedron|polyhedral]] prism is a 4-dimensional prism made from two translated polyhedra connected by 3-dimensional prism cells. A regular polyhedron {''p'', ''q''} can construct the uniform polychoric prism, represented by the product {''p'', ''q''}×{}. If the polyhedron is a cube, and the sides are cubes, it becomes a [[tesseract]]: {4, 3}×{} = {{nowrap|{4, 3, 3}.}} |
|||
**[[Image:Dodecahedral prism.png|50px]]Example: [[Dodecahedral prism]], {5, 3}×{}, two parallel [[dodecahedron|dodecahedra]] connected by 12 pentagonal prism ''sides''. |
|||
Higher order prismatic polytopes also exist as [[cartesian product]]s of any two polytopes. The dimension of a product polytope is the product of the dimensions of its elements. The first examples of these exist in 4-dimensional space; they are called [[duoprism]]s as the product of two polygons. Regular duoprisms are represented as {''p''}×{''q''}. |
|||
== Галерија == |
== Галерија == |
||
| Ред 31: | Ред 233: | ||
Датотека:Prism.svg|Коса неправила призма |
Датотека:Prism.svg|Коса неправила призма |
||
</gallery> |
</gallery> |
||
== Референце == |
|||
{{Reflist|}} |
|||
== Литература == |
|||
{{Refbegin|30em}} |
|||
* {{cite book | author= Anthony Pugh | year= 1976 | title= Polyhedra: A visual approach | publisher= University of California Press Berkeley | location= California | isbn= 0-520-03056-7 }} |
|||
* Љиљана Петрушевски - Полиедри |
|||
* Cromwell, P.;''Polyhedra'', CUP hbk (1997), pbk. (1999). |
|||
* {{cite book| author1 = Grünbaum, B. | authorlink1 = Branko Grünbaum | chapter = Polyhedra with Hollow Faces |
|||
| editor1 = Tibor Bisztriczky | editor2 = Peter McMullen |
|||
| editor3 = Rolf Schneider |display-editors = 3 | editor4 = A Weiss |
|||
| title = Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational |
|||
| year = 1994| publisher = Springer | location = |isbn= 978-94-010-4398-4| pages = 43–70 |
|||
| url = http://link.springer.com/chapter/10.1007/978-94-011-0924-6_3}} |
|||
* Grünbaum, B.; Are your polyhedra the same as my polyhedra? ''Discrete and comput. geom: the Goodman-Pollack festschrift'', ed. Aronov et al. Springer (2003) pp. 461–488.'' ([http://www.math.washington.edu/~grunbaum/Your%20polyhedra-my%20polyhedra.pdf pdf] {{Wayback|url=http://www.math.washington.edu/~grunbaum/Your%20polyhedra-my%20polyhedra.pdf |date=20160803160413 }}) |
|||
* [[Joseph Louis François Bertrand|Bertrand, J.]] (1858). Note sur la théorie des polyèdres réguliers, ''Comptes rendus des séances de l'Académie des Sciences'', '''46''', pp. 79–82. |
|||
* Haeckel, E. (1904). ''[[Kunstformen der Natur]]''. Available as Haeckel, E. ''Art forms in nature'', Prestel USA (1998), {{isbn|3-7913-1990-6}}, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html |
|||
*Smith, J. V. (1982). ''Geometrical And Structural Crystallography''. John Wiley and Sons. |
|||
* [[Duncan MacLaren Young Sommerville|Sommerville, D. M. Y.]] (1930). ''An Introduction to the Geometry of n Dimensions.'' E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes. |
|||
*[[H.S.M. Coxeter|Coxeter, H.S.M.]]; Regular Polytopes (third edition). Dover Publications Inc. {{isbn|0-486-61480-8}} |
|||
* {{cite journal |authorlink=Hassler Whitney |first=Hassler |last=Whitney |title=Congruent graphs and the connectivity of graphs |url=https://archive.org/details/sim_american-journal-of-mathematics_1932-01_54_1/page/150 |journal=Amer. J. Math. |volume=54 |issue=1 |pages=150–168 |year=1932 |jstor=2371086 |doi=10.2307/2371086|hdl=10338.dmlcz/101067 }} |
|||
* {{citation |
|||
| last1 = Blind | first1 = Roswitha |
|||
| last2 = Mani-Levitska | first2 = Peter |
|||
| doi = 10.1007/BF01830678 |
|||
| issue = 2–3 |
|||
| journal = [[Aequationes Mathematicae]] |
|||
| mr = 921106 |
|||
| pages = 287–297 |
|||
| title = Puzzles and polytope isomorphisms |
|||
| volume = 34 |
|||
| year = 1987}} |
|||
* {{citation |
|||
| last = Kalai | first = Gil | authorlink = Gil Kalai |
|||
| doi = 10.1016/0097-3165(88)90064-7 |
|||
| issue = 2 |
|||
| journal = [[Journal of Combinatorial Theory]] | series = Ser. A |
|||
| mr = 964396 |
|||
| pages = 381–383 |
|||
| title = A simple way to tell a simple polytope from its graph |
|||
| volume = 49 |
|||
| year = 1988}} |
|||
* {{cite journal |first=Volker |last=Kaibel |first2=Alexander |last2=Schwartz |url=http://eprintweb.org/S/authors/All/ka/Kaibel/16 |title=On the Complexity of Polytope Isomorphism Problems |journal=[[Graphs and Combinatorics]] |volume=19 |issue=2 |pages=215–230 |year=2003 |arxiv=math/0106093 |doi=10.1007/s00373-002-0503-y |url-status=dead |archiveurl=https://web.archive.org/web/20150721175904/http://eprintweb.org/S/authors/All/ka/Kaibel/16 |archivedate=2015-07-21 }} |
|||
* {{Cite book | last1 = Büeler | first1 = B. | last2 = Enge | first2 = A. | last3 = Fukuda | first3 = K. | doi = 10.1007/978-3-0348-8438-9_6 | chapter = Exact Volume Computation for Polytopes: A Practical Study | title = Polytopes — Combinatorics and Computation | pages = 131 | year = 2000 | isbn = 978-3-7643-6351-2 | pmid = | pmc = }} |
|||
* {{citation |
|||
| last = Yao | first = Andrew Chi Chih | authorlink = Andrew Yao |
|||
| doi = 10.1145/322276.322289 |
|||
| issue = 4 |
|||
| journal = [[Journal of the ACM]] |
|||
| mr = 677089 |
|||
| pages = 780–787 |
|||
| title = A lower bound to finding convex hulls |
|||
| volume = 28 |
|||
| year = 1981}}; {{citation |
|||
| last = Ben-Or | first = Michael |
|||
| contribution = Lower Bounds for Algebraic Computation Trees |
|||
| doi = 10.1145/800061.808735 |
|||
| pages = 80–86 |
|||
| title = Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83) |
|||
| year = 1983}} |
|||
* {{citation |
|||
| last1 = Cundy | first1 = H. Martyn | author1-link = Martyn Cundy |
|||
| last2 = Rollett | first2 = A. P. |
|||
| edition = 2nd |
|||
| location = Oxford |
|||
| mr = 0124167 |
|||
| publisher = Clarendon Press |
|||
| title = Mathematical Models |
|||
| year = 1961}}. |
|||
* {{citation |
|||
| last1 = Gailiunas | first1 = P. |
|||
| last2 = Sharp | first2 = J. |
|||
| doi = 10.1080/00207390500064049 |
|||
| issue = 6 |
|||
| journal = International Journal of Mathematical Education in Science and Technology |
|||
| pages = 617–642 |
|||
| title = Duality of polyhedra |
|||
| volume = 36 |
|||
| year = 2005}}. |
|||
* {{citation |
|||
| last = Grünbaum | first = Branko | authorlink = Branko Grünbaum |
|||
| editor1-last = Aronov | editor1-first = Boris | editor1-link = Boris Aronov |
|||
| editor2-last = Basu | editor2-first = Saugata |
|||
| editor3-last = Pach | editor3-first = János | editor3-link = János Pach |
|||
| editor4-last = Sharir | editor4-first = Micha | editor4-link = Micha Sharir |
|||
| contribution = Are your polyhedra the same as my polyhedra? |
|||
| doi = 10.1007/978-3-642-55566-4_21 |
|||
| mr = 2038487 |
|||
| pages = 461–488 |
|||
| publisher = Springer | location = Berlin |
|||
| series = Algorithms and Combinatorics |
|||
| title = Discrete and Computational Geometry: The Goodman–Pollack Festschrift |
|||
| volume = 25 |
|||
| year = 2003| citeseerx = 10.1.1.102.755| isbn = 978-3-642-62442-1 }}. |
|||
* {{citation |
|||
| last = Grünbaum | first = Branko | authorlink = Branko Grünbaum |
|||
| doi = 10.1016/j.disc.2005.09.037 |
|||
| issue = 3–5 |
|||
| journal = [[Discrete Mathematics (journal)|Discrete Mathematics]] |
|||
| mr = 2287486 |
|||
| pages = 445–463 |
|||
| title = Graphs of polyhedra; polyhedra as graphs |
|||
| volume = 307 |
|||
| year = 2007}}. |
|||
* {{citation |
|||
| last1 = Grünbaum | first1 = Branko | author1-link = Branko Grünbaum |
|||
| last2 = Shephard | first2 = G. C. | author2-link = Geoffrey Colin Shephard |
|||
| editor-last = Senechal | editor-first = Marjorie | editor-link = Marjorie Senechal |
|||
| contribution = Duality of polyhedra |
|||
| doi = 10.1007/978-0-387-92714-5_15 |
|||
| isbn = 978-0-387-92713-8 |
|||
| mr = 3077226 |
|||
| pages = 211–216 |
|||
| publisher = Springer | location = New York |
|||
| title = Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination |
|||
| year = 2013}}. |
|||
* {{citation| first=Magnus | last=Wenninger | authorlink=Magnus Wenninger | title=Dual Models | publisher=Cambridge University Press | year=1983 | isbn=0-521-54325-8 | mr = 0730208}}. |
|||
* {{citation |
|||
| last1 = Barvinok | first1 = Alexander |
|||
| isbn = 0821829688 |
|||
| publisher = American Mathematical Soc. | location = Providence |
|||
| title = A course in convexity |
|||
| year = 2002}} |
|||
{{refend}} |
|||
== Спољашње везе == |
== Спољашње везе == |
||
{{Commonscat|Prisms (geometry)}} |
{{Commonscat|Prisms (geometry)}} |
||
{{EB1911 poster|Prism<!--|volume=22|page=361-->}} |
|||
*{{MathWorld |urlname=Prism |title=Prism}} |
|||
*[http://www.korthalsaltes.com/selecion.php?sl=selecion3 Paper models of prisms and antiprisms] Free nets of prisms and antiprisms |
|||
*[https://web.archive.org/web/20141019220935/http://www.software3d.com/Prisms.php Paper models of prisms and antiprisms] Using nets generated by ''[[Stella (software)|Stella]]'' |
|||
{{нормативна контрола}} |
{{нормативна контрола}} |
||
Верзија на датум 20. јул 2022. у 20:38
Један корисник управо ради на овом чланку. Молимо остале кориснике да му допусте да заврши са радом. Ако имате коментаре и питања у вези са чланком, користите страницу за разговор.
Хвала на стрпљењу. Када радови буду завршени, овај шаблон ће бити уклоњен. Напомене
|
| Set of uniform n-gonal prisms | |
|---|---|
 Example uniform hexagonal prism | |
| Type | uniform in the sense of semiregular polyhedron |
| Стране | 2 n-gonal regular polygons n squares |
| Ивице | 3n |
| Темена | 2n |
| Конфигурација темена | 4.4.n |
| Шлафлијев симбол | {n}×{} [1] t{2, n} |
| Конвејова нотација | Pn |
| Кокстеров дијаграм | |
| Група симетрије | Dnh, [n,2], (*n22), order 4n |
| Група ротације | Dn, [n,2]+, (n22), order 2n |
| Дуални полиедар | convex dual-uniform n-gonal bipyramid |
| Својства | convex, regular polygon faces, vertex-transitive, translated bases, sides ⊥ bases |
| Мрежа | |
 | |
Призма је геометријски полиедар ограничен са две паралелне подударне основе (основа може бити било који многоугао) које су повезане паралелограмима (бочним странама). У зависности од многоугла у основи, призма може бити троугаона, четвороугаона, петоугаона итд. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.
Like many basic geometric terms, the word prism (од грчки πρίσμα (prisma), са значењем „something sawed”) was first used in Euclid's Elements. Euclid defined the term in Book XI as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. However, this definition has been criticized for not being specific enough in relation to the nature of the bases, which caused confusion among later geometry writers.[2][3]
Right prism, uniform prism
Right prism
A right prism is a prism in which the joining edges and faces are perpendicular to the base faces.[4] This applies if all the joining faces are rectangular.
The dual of a right n-prism is a right n-bipyramid.
A right prism (with rectangular sides) with regular n-gon bases has Schläfli symbol { }×{n}. It approaches a cylindrical solid as n approaches infinity.
Special cases
- A right rectangular prism (with a rectangular base) is also called a cuboid, or informally a rectangular box. A right rectangular prism has Schläfli symbol { }×{ }×{ }.
- A right square prism (with a square base) is also called a square cuboid, or informally a square box.
Note: some texts may apply the term rectangular prism or square prism to both a right rectangular-based prism and a right square-based prism.
Uniform prism
A uniform prism or semiregular prism is a right prism with regular bases and square sides, since such prisms are in the set of uniform polyhedra.
A uniform n-gonal prism has Schläfli symbol t{2,n}.
Right prisms with regular bases and equal edge lengths form one of the two infinite series of semiregular polyhedra, the other series being antiprisms.
Подела
- Праве и косе призме
- Тростране, четворостране, петостране ...
- Правилне и неправилне
Правилна призма је она призма која у основи има правилан многоугао (троугао, четвороугао, петоугао итд.)
Делови призме
- Права
- Основа (Basis)
- Бочна страна
- Основна ивица
Површина призме
Површина призме је збир површина свих страна призме. Најједноставније је израчунати површину бочних страна -М- призме и саберемо са две основе.
where B is the area of the base, h the height, and P the base perimeter.
The surface area of a right prism whose base is a regular n-sided polygon with side length s and height h is therefore:
Запремина призме
Запремину призме израчунавамо тако што површину основе призме помножимо висином призме.
where B is the base area and h is the height. The volume of a prism whose base is an n-sided regular polygon with side length s is therefore:
Schlegel diagrams
 P3 |
 P4 |
 P5 |
 P6 |
 P7 |
 P8 |
Symmetry
The symmetry group of a right n-sided prism with regular base is Dnh of order 4n, except in the case of a cube, which has the larger symmetry group Oh of order 48, which has three versions of D4h as subgroups. The rotation group is Dn of order 2n, except in the case of a cube, which has the larger symmetry group O of order 24, which has three versions of D4 as subgroups.
The symmetry group Dnh contains inversion iff n is even.
The hosohedra and dihedra also possess dihedral symmetry, and an n-gonal prism can be constructed via the geometrical truncation of an n-gonal hosohedron, as well as through the cantellation or expansion of an n-gonal dihedron.
Truncated prism
A truncated prism is a prism with non-parallel top and bottom faces.[5]

Twisted prism
A twisted prism is a nonconvex polyhedron constructed from a uniform n-prism with each side face bisected on the square diagonal, by twisting the top, usually by π/n radians (180/n degrees) in the same direction, causing sides to be concave.[6][7]
A twisted prism cannot be dissected into tetrahedra without adding new vertices. The smallest case: the triangular form, is called a Schönhardt polyhedron.
An n-gonal twisted prism is topologically identical to the n-gonal uniform antiprism, but has half the symmetry group: Dn, [n,2]+, order 2n. It can be seen as a nonconvex antiprism, with tetrahedra removed between pairs of triangles.
| 3-gonal | 4-gonal | 12-gonal | |
|---|---|---|---|
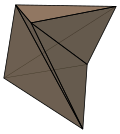 Schönhardt polyhedron |
 Twisted square prism |
 Square antiprism |
 Twisted dodecagonal antiprism |
Frustum
A frustum is a similar construction to a prism, with trapezoid lateral faces and differently sized top and bottom polygons.

Star prism
A star prism is a nonconvex polyhedron constructed by two identical star polygon faces on the top and bottom, being parallel and offset by a distance and connected by rectangular faces. A uniform star prism will have Schläfli symbol {p/q} × { }, with p rectangle and 2 {p/q} faces. It is topologically identical to a p-gonal prism.
| { }×{ }180×{ } | ta{3}×{ } | {5/2}×{ } | {7/2}×{ } | {7/3}×{ } | {8/3}×{ } | |
|---|---|---|---|---|---|---|
| D2h, order 8 | D3h, order 12 | D5h, order 20 | D7h, order 28 | D8h, order 32 | ||

|

|

|

|

|

|
|
Crossed prism
A crossed prism is a nonconvex polyhedron constructed from a prism, where the vertices of one base are inverted around the center of this base (or rotated by 180°). This transforms the side rectangular faces into crossed rectangles. For a regular polygon base, the appearance is an n-gonal hour glass. All oblique edges pass through a single body center. Note: no vertex is at this body centre. A crossed prism is topologically identical to an n-gonal prism.
| { }×{ }180×{ }180 | ta{3}×{ }180 | {3}×{ }180 | {4}×{ }180 | {5}×{ }180 | {5/2}×{ }180 | {6}×{ }180 | |
|---|---|---|---|---|---|---|---|
| D2h, order 8 | D3d, order 12 | D4h, order 16 | D5d, order 20 | D6d, order 24 | |||

|

|

|

|

|

|

|

|
Toroidal prism
A toroidal prism is a nonconvex polyhedron like a crossed prism, but without bottom and top base faces, and with simple rectangular side faces closing the polyhedron. This can only be done for even-sided base polygons. These are topological tori, with Euler characteristic of zero. The topological polyhedral net can be cut from two rows of a square tiling (with vertex configuration 4.4.4.4): a band of n squares, each attached to a crossed rectangle. An n-gonal toroidal prism has 2n vertices, 2n faces: n squares and n crossed rectangles, and 4n edges. It is topologically self-dual.
| D4h, order 16 | D6h, order 24 |
| v=8, e=16, f=8 | v=12, e=24, f=12 |

|

|
Prismatic polytope
A prismatic polytope is a higher-dimensional generalization of a prism. An n-dimensional prismatic polytope is constructed from two (n − 1)-dimensional polytopes, translated into the next dimension.
The prismatic n-polytope elements are doubled from the (n − 1)-polytope elements and then creating new elements from the next lower element.
Take an n-polytope with fi i-face elements (i = 0, ..., n). Its (n + 1)-polytope prism will have 2fi + fi−1 i-face elements. (With f−1 = 0, fn = 1.)
By dimension:
- Take a polygon with n vertices, n edges. Its prism has 2n vertices, 3n edges, and 2 + n faces.
- Take a polyhedron with v vertices, e edges, and f faces. Its prism has 2v vertices, 2e + v edges, 2f + e faces, and 2 + f cells.
- Take a polychoron with v vertices, e edges, f faces, and c cells. Its prism has 2v vertices, 2e + v edges, 2f + e faces, 2c + f cells, and 2 + c hypercells.
Uniform prismatic polytope
A regular n-polytope represented by Schläfli symbol {p, q, ..., t} can form a uniform prismatic (n + 1)-polytope represented by a Cartesian product of two Schläfli symbols: {p, q, ..., t}×{}.
By dimension:
- A 0-polytopic prism is a line segment, represented by an empty Schläfli symbol {}.
- A 1-polytopic prism is a rectangle, made from 2 translated line segments. It is represented as the product Schläfli symbol {}×{}. If it is square, symmetry can be reduced: {}×{} = {4}.
- A polygonal prism is a 3-dimensional prism made from two translated polygons connected by rectangles. A regular polygon {p} can construct a uniform n-gonal prism represented by the product {p}×{}. If p = 4, with square sides symmetry it becomes a cube: {4}×{} = {4, 3}.
 Example: Pentagonal prism, {5}×{}, two parallel pentagons connected by 5 rectangular sides.
Example: Pentagonal prism, {5}×{}, two parallel pentagons connected by 5 rectangular sides.
- A polyhedral prism is a 4-dimensional prism made from two translated polyhedra connected by 3-dimensional prism cells. A regular polyhedron {p, q} can construct the uniform polychoric prism, represented by the product {p, q}×{}. If the polyhedron is a cube, and the sides are cubes, it becomes a tesseract: {4, 3}×{} = {4, 3, 3}.
 Example: Dodecahedral prism, {5, 3}×{}, two parallel dodecahedra connected by 12 pentagonal prism sides.
Example: Dodecahedral prism, {5, 3}×{}, two parallel dodecahedra connected by 12 pentagonal prism sides.
Higher order prismatic polytopes also exist as cartesian products of any two polytopes. The dimension of a product polytope is the product of the dimensions of its elements. The first examples of these exist in 4-dimensional space; they are called duoprisms as the product of two polygons. Regular duoprisms are represented as {p}×{q}.
Галерија
-
Права тространа призма
-
Коса неправила призма
Референце
- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3b
- ^ Thomas Malton (1774). A Royal Road to Geometry: Or, an Easy and Familiar Introduction to the Mathematics. ... By Thomas Malton. ... author, and sold. стр. 360—.
- ^ James Elliot (1845). Key to the Complete Treatise on Practical Geometry and Mensuration: Containing Full Demonstrations of the Rules ... Longman, Brown, Green, and Longmans. стр. 3—.
- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p.28
- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p.81
- ^ The facts on file: Geometry handbook, Catherine A. Gorini, 2003, ISBN 0-8160-4875-4, p.172
- ^ „Pictures of Twisted Prisms”.
Литература
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
- Љиљана Петрушевски - Полиедри
- Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
- Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ур.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. стр. 43—70. ISBN 978-94-010-4398-4.
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Архивирано на сајту Wayback Machine (3. август 2016))
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067.
- Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678
- Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7
- Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093
 . doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г.
. doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г. - Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. стр. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6.
- Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), стр. 80—86, doi:10.1145/800061.808735
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd изд.), Oxford: Clarendon Press, MR 0124167.
- Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049.
- Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ур.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, стр. 461—488, CiteSeerX 10.1.1.102.755
 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21.
, ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21. - Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037.
- Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ур.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, стр. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208.
- Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688
Спољашње везе
- Weisstein, Eric W. „Prism”. MathWorld.
- Paper models of prisms and antiprisms Free nets of prisms and antiprisms
- Paper models of prisms and antiprisms Using nets generated by Stella