Полиедар
Полиедар је геометријско тело омеђено са четири или више многоуглова (који се називају стране или пљоснати полиедри) и коме су ивице дужи. Сама реч је настала као сложеница речи поли (πολυς), што значи много, и речи едрон (εδρον), што значи база, површ, седиште.[1]
Полиедарска површ[уреди | уреди извор]
Скуп површи многоуглова таквих да је свака страница сваког многоугла уједно и страница још само једног многоугла, образују затворену површ која се назива полиедарска површ. Део геометријског простора који ограничава (затворена) полиедарска површ је унутрашњост полиедарске површи.
Унија полиедарске површи и њене унутрашњости је полиедар.
- Површи многоуглова, од којих се састоји полиедарска површ, називају се стране (или пљосни) полиедра, а странице тих многоуглова називају се ивице полиедарске површи и полиедра.
- Рогљеви које образују стране полиедра са једним заједничким теменом су рогљеви полиедра, а врхови тих рогљева су темена полиедра.
- Свака дуж која спаја два темена полиедра, а не припада ниједној страни полиедра представља дијагоналу полиедра.
- Свака раван коју одређују три темена полиедра и не садржи ниједну страну полиедра представља дијагоналну раван полиедра.
Подела полиедра[уреди | уреди извор]
Полиедри могу бити конвексни и неконвексни-конкавни.
- Полиедар је конвексан уколико свака дуж која спаја његове две произвољне тачке припада том полиедру, у супротном случају полиедар је неконвексан односно конкаван.
Конвексни Полиедри[уреди | уреди извор]
- Конвексан полиедар лежи само са једне стране равни сваке своје стране.
- Конвексан полиедар се може представити као пресек коначног броја полупростора одређених равнима његових страна.
Регуларни полиедри[уреди | уреди извор]
Полиедар чије су све стране регуларни подударни многоуглови и чији су сви рогљеви подударни назива се регуларан полиедар.
Конвексни регуларни полиедри - Платонова тела[уреди | уреди извор]
Конвексни регуларни полиедри су познати под називом Платонова тела. Њихове стране су подударни правилни многоуглови, а рогљеви су међусобно подударни и конвексни. То значи да су све стране једног полиедра правилни многоуглови са истим бројем n међусобно једнаких страница и у темену сваког рогља се сустиче исти број k тих многоуглова.
Дуални полиедри[уреди | уреди извор]
У геометрији полиедри се посматрају у паровима. Сваком полиедру одговара дуални полиедар који настаје метаморфозом датог полиедра у којој:
- сваком темену полазног полиедра одговара страна новог полиедра
- свакој страни полазног полиедра одговара теме новог полиедра
- свакој ивици полазног полиедра одговара ивица новог полиедра.
Особине[уреди | уреди извор]
- Страна прелази у теме новог полиедра, а њено теме у страну која садржи то теме.
- Теме прелази у страну новог полиедра, а свака страна чије је то теме у теме те стране.
- Ивица која спаја два темена прелази у заједничку ивицу две одговарајуће стране новог полиедра.
- Заједничка ивица две суседне стране полиедра прелази у ивицу која спаја одговарајућа темена новог полиедра.
- Свака страна полиедра је полигон са одређеним бројем својих темена. Метаморфозом полигон прелази у теме, а његова темена у стране новог полиедра чије је то теме, односно страни одовара рогаљ.
- Свако теме полиедра је теме једног његовог рогља. Теме прелази у страну, а стране полиедра које се сустичу у том темену (стране рогља) у темена која припадају тој страни новог полиедра.
- Дуални полиедар дуалног полиедра је полазни полиедар.
Дуални полиедри – Платонова тела[уреди | уреди извор]
Стране конвексног регуларног полиедра типа {n, k} су правилни полигони са n темена. Страна се пресликава у теме новог полиедра a, а њена темена у стране новог полиедра које се сустичу у том темену. Добија се рогаљ са n страна.
Темена конвексног регуларног полиедра типа су {n, k} су темена подударних рогљева са k страна. Теме рогља прелази у страну, а његове стране (односно стране полиедра које се сустичу у том темену) у k темена те стране новог полиедра.
- Дуални полиедар конвексног регуларног полиедра типа {n, k} је конвексни регуларни полиедар типа {k, n}.
Нумеричке карактеристике Платонових тела[уреди | уреди извор]
Карактеристика полиедра:
- n – број темена (страница) стране полиедра
- k – број страна које се сустичу у истом темену
- T – број темена полиедра
- S – број страна полиедра
- I – број ивица полиедра
Диедар чине две суседне стране са заједничком ивицом која представља ивицу диедра. Сви диедрални углови једног Платоновог тела су међусобно једнаки. Диедрални угао се очитава у равни нормалној на ивицу диедра.
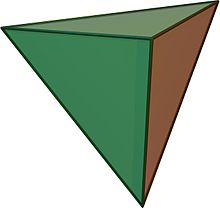
Платонова тела - тетраедар[уреди | уреди извор]
- 4 темена
- 6 ивица
- 4 стране
- Диедрални угао: 70.53°
Формуле[уреди | уреди извор]
| Површина | |
| Запремина | |
| Полупречник описане сфере | |
| Полупречник уписане сфере | |
| Висина | |
| Угао између ивице и површи | |
| Угао између две површи |
Платонова тела – хексаедар[уреди | уреди извор]

- 8 темена
- 12 ивица
- 6 страна
- Диедрални угао: 90°
Формуле[уреди | уреди извор]

| Површина | |
| Запремина | |
| Мала дијагонала[2] | |
| Велика дијагонала | |
| Полупречник уписане сфере | |
| Полупречник описане сфере |
Платонова тела – октаедар[уреди | уреди извор]

- 6 темена
- 12 ивица
- 8 страна
- Диедрални угао: 109.47°
Формуле[уреди | уреди извор]
| Површина | |
| Запремина | |
| Полупречник описане сфере |
|
| Полупречник уписане сфере |
Платонова тела – додекаедар[уреди | уреди извор]

- 20 темена
- 30 ивица
- 12 страна
- Диедрални угао: 116.56°
Формуле[уреди | уреди извор]
| Површина | |
| Запремина | |
| Полупречник уписане сфере |
|
| Полупречник описане сфере |
Платонова тела – икосаедар[уреди | уреди извор]

- 12 темена
- 30 ивица
- 20 страна
- Диедрални угао: 138.19°
Формуле[уреди | уреди извор]
| Површина | |
| Запремина | |
| Полупречник уписане сфере |
|
| Полупречник описане сфере |
Изометрија полиедра[уреди | уреди извор]
Узајамно једнозначно пресликавање f: T1 → T2 полиедара (тела) T1, T2 у коме долази до очувања метрике односно очувања растојања између тачака је изометрично пресликавање или изометрија. Геометријске трансформације: транслација, ротација, рефлексија и њихова композиција (узастопно извођење) у произвољном поретку и произвољном броју су изометричне трансформације.
Симетрије полиедра[уреди | уреди извор]
Изометрично пресликавање f : T → T полиедара T у самог себе је симетрија. Група симетрија сваког полиедра садржи све могуће ротације и све могуће рефлексије које полиедар пресликавају у самог себе. Композиција симетрија једног полиедра (у произвољном поретку) је такође једна симетрија из групе свих могућих симетрија тог полиедра.
Референце[уреди | уреди извор]
Литература[уреди | уреди извор]
- Љиљана Петрушевски - Полиедри
- Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
- Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ур.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. стр. 43—70. ISBN 978-94-010-4398-4.
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Архивирано на сајту Wayback Machine (3. август 2016))
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067.
- Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678
- Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7
- Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093
 . doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г.
. doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г. - Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. стр. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6.
- Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), стр. 80—86, doi:10.1145/800061.808735
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd изд.), Oxford: Clarendon Press, MR 0124167.
- Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049.
- Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ур.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, стр. 461—488, CiteSeerX 10.1.1.102.755
 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21.
, ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21. - Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037.
- Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ур.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, стр. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208.
- Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688
Спољашње везе[уреди | уреди извор]
Општа теорија[уреди | уреди извор]
- Weisstein, Eric W. „Polyhedron”. MathWorld.
- Polyhedra Pages
- Uniform Solution for Uniform Polyhedra by Dr. Zvi Har'El
- Symmetry, Crystals and Polyhedra
Списак и база података полиедара[уреди | уреди извор]
- Virtual Reality Polyhedra - The Encyclopedia of Polyhedra
- Electronic Geometry Models - Contains a peer reviewed selection of polyhedra with unusual properties.
- Polyhedron Models - Virtual polyhedra
- Paper Models of Uniform (and other) Polyhedra
Слободни софтвер[уреди | уреди извор]
- A Plethora of Polyhedra – An interactive and free collection of polyhedra in Java. Features includes nets, planar sections, duals, truncations and stellations of more than 300 polyhedra.
- Hyperspace Star Polytope Slicer - Explorer java applet, includes a variety of 3d viewer options.
- openSCAD - Free cross-platform software for programmers. Polyhedra are just one of the things you can model. The openSCAD User Manual is also available.
- OpenVolumeMesh - An open source cross-platform C++ library for handling polyhedral meshes. Developed by the Aachen Computer Graphics Group, RWTH Aachen University.
- Polyhedronisme Архивирано на сајту Wayback Machine (25. април 2012) - Web-based tool for generating polyhedra models using Conway Polyhedron Notation. Models can be exported as 2D PNG images, or as 3D OBJ or VRML2 files. The 3D files can be opened in CAD software, or uploaded for 3D printing at services such as Shapeways.
Ресурси за прављење физичких модела[уреди | уреди извор]
- Paper Models of Polyhedra Free nets of polyhedra
- Simple instructions for building over 30 paper polyhedra
- Polyhedra plaited with paper strips - Polyhedra models constructed without use of glue.

























