Talesova teorema

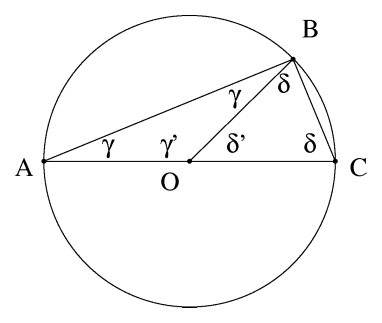
U geometriji, Talesov stav (dobio ime po Talesu iz Mileta) tvrdi da ako su A, B i C tačke na krugu gde je AC prečnik kruga, tada je ugao ABC prav ugao.
Dokaz[uredi | uredi izvor]
Koristimo sledeće pretpostavke: Zbir uglova u trouglu je jednak zbiru dva prava ugla i dva ugla jednakokrakog trougla su jednaka.
Neka je O centar kruga. Neka su OA = OB = OC, OAB i OBC su jednakokraki trouglovi, i po jednakosti uglova jednakokrakog trougla, OBC = OCB i BAO = ABO. Neka γ = BAO i δ = OBC.
- 2γ + γ ′ = 180°
i
- 2δ + δ ′ = 180°
Takođe znamo da
- γ ′ + δ ′ = 180°
Dodajući prve dve jednačine i zamenjujući treću sledi da
- 2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°
što nakon skraćivanja, γ ′ i δ ′, dokazuje da
- γ + δ = 90°
Generalizacija[uredi | uredi izvor]
Talesova teorema je specijalni slučaj sledeće teoreme: Ako se tri tačke A, B i C nalaze na krugu sa centrom O, ugao AOC je dva puta veći od ugla ABC.
Talesova teorema za slične trouglove[uredi | uredi izvor]

U školskoj literaturu se upravo ova teorema slovi za Talesovu i glasi: U sistemu sličnih trouglova odnos naleglih stranica za dati ugao je isti kao odnos naspramnih stranica..
Dokaz[uredi | uredi izvor]
Posmatraćemo odnos površina trouglova:

Primetimo da trouglovi i imaju istu visinu spuštenu iz temena V na duž OA u prvom, odnosno OA1 u drugom, tako da odnos njihovih površina predstavlja odnos osnovica datih trouglova, tj. važi:, slično je za par trouglova ΔOAB i
.
Jasno je da je POAB = POBA, jer je reč o istom trouglu, pa nam ostaje da pokažemo da je
Ovo poslednje tvrđenje se lako dokazuje ako primetimo da crveni i plavi trougao imaju iste površine zbog iste osnovice i iste visine, pa su prema tome i komplementi i istih površina iz čega sledi početno tvrđenje.
Sada imamo . Za nastavak dokaza bismo mogli da u trouglu uzmemo zajedničko teme ili A1 ili V1, povučemo naspram njega paralelu naspramnoj stranici i ponovimo postupak.
Istorija[uredi | uredi izvor]
Tales nije bio prvi koji je poznavao ovu činjenicu, jer su je Egipćani i Vavilonci poznavali empirijski. U svakom slučaju oni nisu znali da dokažu ovu teoremu, niti su poznavali pojam dokazivanja niti ih je to uopšte zanimalo. Tako je teorema dobila ime po Talesu koji ju je prvi dokazao.