Круг

Круг је у еуклидској планиметрији геометријско место тачака у равни које се налазе на растојању мањем или једнаком некој задатој дужини од неке дате тачке у истој тој равни. Поменута тачка се зове центром а поменута дужина полупречником круга. Круг је оивичен линијом која се зове кружница и дели раван на унутрашњост круга, саму себе и спољашњост круга. Сама кружница припада кругу кога оивичава.
Двострука дужина полупречника се назива пречником круга, а обим круга је дужина његове кружнице. Други називи са полупречник и пречник су, тим редом, радијус и дијаметар.
Дефиниција[уреди | уреди извор]
- Круг с центром O и полупречником (радијусом) r је геометријско место тачака равни чија растојања од тачке О нису већа од r, тј. то је скуп тачака M равни за које важи . Круг је затворен скуп тачака равни, чија је граница периферија круга, тј. кружница.
- Велики круг лопте (сфере) је круг који се добија пресеком лопте са равни која пролази кроз њен центар. Полупречник В. к. л. је једнак полупречнику лопте. Кроз сваке две тачке лопте које нису крајеви њеног пречника пролази само један В. к. л. Било која два В. к. л. секу се у двема дијаметрално супротним тачкама лопте.
- У нашој математичкој терминологији се под појмом круг понекад подразумева и кружница (дакле крива).
- Круг кривине (диференцијална геометрија) је исто што и оскулаторни круг, тј. оскулаторна кружница.
Остале дефиниције[уреди | уреди извор]
- Круг конвергенције степеног реда:
је круг полупречника R с центром у тачки z-c комплексне равни у чијим свим унутрашњим тачкама z-a|<R) степени ред апсолутно конвергира. Полупречник R круга конвергенције се назива полупречник конвергенције степеног реда. На рубу круга конвергенције степеног реда постоји сингуларна тачка. Може се десити да полупречник конвергенције степеног реда буде нула или бесконачан. Кад је он бесконачан, степени ред конвергира у свакој тачки комплексне равни. За сваки степени ред област конвергенције је увек круг из којег се евентуално искључује неки скуп тачака на његовом рубу.
Аналитичка геометрија[уреди | уреди извор]
У x-y координатном систему, круг са центром (p, q) и полупречником r је скуп свих тачака (x, y) тако да
Ако је круг са центром у координатном почетку, тј. (0, 0), онда се ова формула може упростити до
Круг са центром у координатном почетку и полупречником 1 се зове јединични круг.
Изражен у поларним координатама (r,Θ), круг полупречника rk са центром у тачки (rc,φ) може да се дефинише као:
Нагиб круга може да се изрази следећом формулом:
Сви кругови су слични; као последица, обим круга и његов полупречник су пропорционални, као што су његова површина и квадрат полупречника. Константа пропорционалности је 2π и π, редом. Другим речима:
- Обим круга =
- Површина круга =
Формула за површину круга може да се изведе из формула за обим круга и површину троугла на следећи начин. Замислите правилни шестоугао подељен на једнаке троуглове, са њиховим врховима у центру шестоугла. Површина шестоугла може да се нађе у формули површине троугла, тако што се сабирају дужине основица свих троуглова, множе се дужином висине троуглова (дужина од средине основице до центра) и деле са 2. Ово је апроксимација површине круга. Онда замислите исту ситуацију, али са осмоуглом и апроксимација ће бити мало ближа површини круга. Како се правилни многоугао са све више страница дели на троуглове, то се и површина многоугла све више ближи површини круга. У лимесу, збир свих основица се приближава обиму 2πr, а висина троуглова се приближава полупречнику r. Када се помноже обим и полупречник и поделе са два, добија се површина πr².
Особине[уреди | уреди извор]

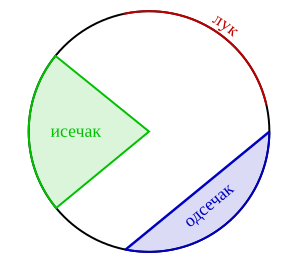
Права која сече кружницу у две тачке је сечица или секанта, а права која додирује круг у једној тачки је тангента. Тангенте су увек под правим углом са полупречницима, сегментима који спајају центар са тачком на кружници, чија се дужина поклапа са дефиницијом од изнад. Део сечице ограничен кругом се зове тетива, а најдужа тетива је она које пролази кроз центар и зове се пречник или дијаметар и чине га два полупречника. Површина дела круга одсеченог тетивом се назива кружни одсечак.
Могуће је наћи највећи број јединствених одсечака које стварају тангенте између тачака на кружници.
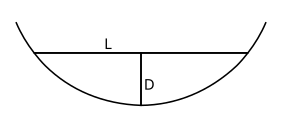
Ако је познат само круг (или његов део), онда његов центар може да се конструише на следећи начин: узму се две не-паралелне тетиве, конструишу се кружне линије на њиховим средиштима и пронађе се пресечна тачка тих линија. Полупречник таквог парцијалног круга може да се израчуна из дужине (L) тетиве и удаљености (D) од средишта тетиве до најближе тачке на кругу по разним формулама, укључујући:
(из математичког извођења)
(из математичког извођења)
Део обима ограничен са два полупречника се зове лук (геометрија), а површина (тј. кришка диска) у оквиру тих полупречника и лука се зове кружни исечак. Однос дужине лука и полупречника дефинише угао између два полупречника у радијанима.
Формула за дужину кружног лука (где је α централни угао над луком):
Формула за површину кружног исечка:
Сваки троугао може да има више кругова: описани круг који садржи сва три темена троугла, уписани круг који је унутар троугла и додирује све три странице, три спољашња круга који су ван троугла и додирују једну страницу и наставке друге две и круг девет тачака који садржи разне важне тачке троугла. Талесова теорема наводи да ако се три темена троугла налазе на кругу где је једна страна троугла пречник круга, онда је супротни угао од те странице прав.
За сваке три различите тачке које леже у равни, а истовремено не леже на правој, постоји тачно један круг чија кружница садржи те тачке (то је заправо описани круг троугла којег дефинишу те тачке). За три одређене тачке <(x1,y1), (x2,y2), (x3,y3)>, једначина овог круга је приказана на једноставан начин користећи матричну детерминанту:
Круг је врста пресека купе, са нултим ексцентрицитетом. У топологији све просте затворене криве су хомеоморфне круговима, а реч круг се често примењује на њима као последица. Тродимензионални аналог кругу је лопта (тело) или сфера (површ).
Квадратура круга се односи на (немогући) задатак конструисања, за дати круг, квадрата са једнаком површином користећи само лењир и шестар. Квадратура круга Тарског је, насупрот, задатак дељења круга на коначно много делова и спајања тих делова да би се сачинио квадрат исте површине. Због аксиоме избора, ово је заиста могуће.
Тродимензионална тела чији су пресеци у неким равнима кругови укључују лопте, сфероиде, ваљке и купе.