Талесова теорема

У геометрији, Талесов став (добио име по Талесу из Милета) тврди да ако су A, B и C тачке на кругу где је AC пречник круга, тада је угао ABC прав угао.

Доказ

Користимо следеће претпоставке: Збир углова у троуглу је једнак збиру два права угла и два угла једнакокраког троугла су једнака.

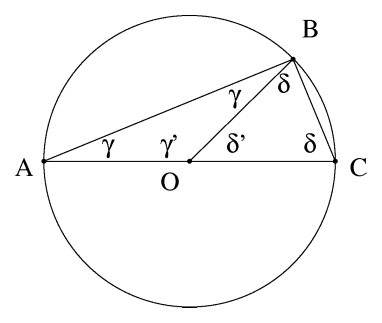
Нека је O центар круга. Нека су OA = OB = OC, OAB и OBC су једнакокраки троуглови, и по једнакости углова једнакокраког троугла, OBC = OCB и BAO = ABO. Нека γ = BAO и δ = OBC.

2γ + γ ′ = 180°

и

2δ + δ ′ = 180°

Такође знамо да

γ ′ + δ ′ = 180°

Додајући прве две једначине и замењујући трећу следи да

2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°

што након скраћивања, γ ′ и δ ′, доказује да

γ + δ = 90°

Генерализација

Талесова теорема је специјални случај следеће теореме: Ако се три тачке A, B и C налазе на кругу са центром O, угао AOC је два пута већи од угла ABC.

Талесова теорема за сличне троуглове

Систем сличних троуглова

У школској литературу се управо ова теорема слови за Талесову и гласи: У систему сличних троуглова однос налеглих страница за дати угао је исти као однос наспрамних страница..${\frac {OA}{OA_{1}}}={\frac {OB}{OB_{1}}}={\frac {AB}{A_{1}B_{1}}}$

Доказ

Посматраћемо однос површина троуглова:${\frac {P_{OBA}}{P_{OBA_{1}}}}={\frac {P_{OAB}}{P_{OAB_{1}}}}$

Једнакост површина троуглова са истом основицом и висином

Приметимо да троуглови $\bigtriangleup _{OBA}$ и $\bigtriangleup _{OBA_{1}}$ имају исту висину спуштену из темена В на дуж ОА у првом, односно ОА₁ у другом, тако да однос њихових површина представља однос основица датих троуглова, тј. важи:${\frac {P_{OBA}}{P_{OBA_{1}}}}={\frac {OA}{OA_{1}}}$, слично је за пар троуглова Δ_ОАБ и $\bigtriangleup _{OAB_{1}}$

${\frac {P_{OAB}}{P_{OAB_{1}}}}={\frac {OB}{OB_{1}}}$.

Јасно је да је P_OAB = P_OBA, јер је реч о истом троуглу, па нам остаје да покажемо да је

$P_{OBA_{1}}=P_{OAB_{1}}$

Ово последње тврђење се лако доказује ако приметимо да црвени и плави троугао имају исте површине због исте основице и исте висине, па су према томе и комплементи $\bigtriangleup _{ABA_{1}}$ и $\bigtriangleup _{ABB_{1}}$истих површина из чега следи почетно тврђење.

Сада имамо ${\frac {OA}{OA_{1}}}={\frac {OB}{OB_{1}}}$. За наставак доказа бисмо могли да у троуглу $\bigtriangleup _{OA_{1}B_{1}}$ узмемо заједничко теме или А₁ или В₁, повучемо наспрам њега паралелу наспрамној страници и поновимо поступак.

Историја

Талес није био први који је познавао ову чињеницу, јер су је Египћани и Вавилонци познавали емпиријски. У сваком случају они нису знали да докажу ову теорему, нити су познавали појам доказивања нити их је то уопште занимало. Тако је теорема добила име по Талесу који ју је први доказао.