Ромб

Ромб
A rhombus in two different orientations
Тип	quadrilateral, trapezoid, parallelogram, kite
Ивице и темена	4
Дијаграм Кокстера
Симетрична група	Dihedral (D2), [2], (*22), order 4
Површина	$K={\frac {p\cdot q}{2}}$ (half the product of the diagonals)
Двоструки многоугао	rectangle
Својства	convex, isotoxal

Ромб је у геометрији четвороугао из класе паралелограма коме су све странице једнаких дужина. Карактерише га произвољна величина угла између две његове стране, која може да варира у реалном интервалу (0,π). Специјалан случај ромба коме су странице нормалне једна на другу је квадрат.

The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after the French sweet – also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle.

Формуле

Ромб и његови значајнији елементи: Темена A, B, C и D, дужине страница a, висина h, дијагонале d₁ и d₂ и углови α и β.

Висина	$h=a\sin \alpha =a\sin \beta$ $h={\frac {d_{1}d_{2}}{2a}}$
Обим	$O=4a$
Површина	$P=ah={\frac {1}{2}}d_{1}d_{2}$
Дијагонале	$d_{1}=2a\sin {\frac {\beta }{2}}=2a\cos {\frac {\alpha }{2}}$ $d_{2}=2a\sin {\frac {\alpha }{2}}=2a\cos {\frac {\beta }{2}}$
Полупречник уписане кружнице	$\rho \,=\,{\frac {1}{2}}\cdot a\cdot \sin \alpha$

Углови

Из једнакости страна следи да су наспрамни углови ромба једнаки, што значи да постоје само две различите величине углова између страна ромба: α и β.

$\angle BAD=\angle DCB,\;\;\angle CBA=\angle ADC$

Са друге стране правило о збиру углова у четвороуглу једнозначно одређује вредност величине другог угла, уколико је први познат, те је ромб одређен само са дужином странице и једним углом:

$\alpha +\beta +\alpha +\beta =2(\alpha +\beta )=360^{\circ }$

$\alpha +\beta =180^{\circ }$

Углови између дијагонала ромба су прави тј. једнаки 90°.

Etymology

The word "rhombus" comes from стгрч. ῥόμβος, meaning something that spins, which derives from the verb ῥέμβω, romanized: rhémbō, meaning "to turn round and round." The word was used both by Euclid and Archimedes, who used the term "solid rhombus" for a bicone, two right circular cones sharing a common base.

The surface we refer to as rhombus today is a cross section of the bicone on a plane through the apexes of the two cones.

Characterizations

A simple (non-self-intersecting) quadrilateral is a rhombus if and only if it is any one of the following:

• a parallelogram in which a diagonal bisects an interior angle
• a parallelogram in which at least two consecutive sides are equal in length
• a parallelogram in which the diagonals are perpendicular (an orthodiagonal parallelogram)
• a quadrilateral with four sides of equal length (by definition)
• a quadrilateral in which the diagonals are perpendicular and bisect each other
• a quadrilateral in which each diagonal bisects two opposite interior angles
• a quadrilateral ABCD possessing a point P in its plane such that the four triangles ABP, BCP, CDP, and DAP are all congruent
• a quadrilateral ABCD in which the incircles in triangles ABC, BCD, CDA and DAB have a common point

Basic properties

Every rhombus has two diagonals connecting pairs of opposite vertices, and two pairs of parallel sides. Using congruent triangles, one can prove that the rhombus is symmetric across each of these diagonals. It follows that any rhombus has the following properties:

• Opposite angles of a rhombus have equal measure.
• The two diagonals of a rhombus are perpendicular; that is, a rhombus is an orthodiagonal quadrilateral.
• Its diagonals bisect opposite angles.

The first property implies that every rhombus is a parallelogram. A rhombus therefore has all of the properties of a parallelogram: for example, opposite sides are parallel; adjacent angles are supplementary; the two diagonals bisect one another; any line through the midpoint bisects the area; and the sum of the squares of the sides equals the sum of the squares of the diagonals (the parallelogram law). Thus denoting the common side as a and the diagonals as p and q, in every rhombus

$\displaystyle 4a^{2}=p^{2}+q^{2}.$

Not every parallelogram is a rhombus, though any parallelogram with perpendicular diagonals (the second property) is a rhombus. In general, any quadrilateral with perpendicular diagonals, one of which is a line of symmetry, is a kite. Every rhombus is a kite, and any quadrilateral that is both a kite and parallelogram is a rhombus.

A rhombus is a tangential quadrilateral. That is, it has an inscribed circle that is tangent to all four sides.

A rhombus. Each angle marked with a black dot is a right angle. The height h is the perpendicular distance between any two non-adjacent sides, which equals the diameter of the circle inscribed. The diagonals of lengths p and q are the red dotted line segments.

Diagonals

The length of the diagonals p = AC and q = BD can be expressed in terms of the rhombus side a and one vertex angle α as

$p=a{\sqrt {2+2\cos {\alpha }}}$

and

$q=a{\sqrt {2-2\cos {\alpha }}}.$

These formulas are a direct consequence of the law of cosines.

Inradius

The inradius (the radius of a circle inscribed in the rhombus), denoted by r, can be expressed in terms of the diagonals p and q as

$r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}},$

or in terms of the side length a and any vertex angle α or β as

$r={\frac {a\sin \alpha }{2}}={\frac {a\sin \beta }{2}}.$

Area

As for all parallelograms, the area K of a rhombus is the product of its base and its height (h). The base is simply any side length a:

$K=a\cdot h.$

The area can also be expressed as the base squared times the sine of any angle:

$K=a^{2}\cdot \sin \alpha =a^{2}\cdot \sin \beta ,$

or in terms of the height and a vertex angle:

$K={\frac {h^{2}}{\sin \alpha }},$

or as half the product of the diagonals p, q:

$K={\frac {p\cdot q}{2}},$

or as the semiperimeter times the radius of the circle inscribed in the rhombus (inradius):

$K=2a\cdot r.$

Another way, in common with parallelograms, is to consider two adjacent sides as vectors, forming a bivector, so the area is the magnitude of the bivector (the magnitude of the vector product of the two vectors), which is the determinant of the two vectors' Cartesian coordinates: K = x₁y₂ – x₂y₁.

Cartesian equation

The sides of a rhombus centered at the origin, with diagonals each falling on an axis, consist of all points (x, y) satisfying

$\left|{\frac {x}{a}}\right|\!+\left|{\frac {y}{b}}\right|\!=1.$

The vertices are at $(\pm a,0)$ and $(0,\pm b).$ This is a special case of the superellipse, with exponent 1.

Other properties

• One of the five 2D lattice types is the rhombic lattice, also called centered rectangular lattice.
• Identical rhombi can tile the 2D plane in three different ways, including, for the 60° rhombus, the rhombille tiling.

As topological square tilings		As 30-60 degree rhombille tiling

• Three-dimensional analogues of a rhombus include the bipyramid and the bicone.
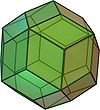
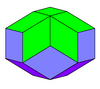
• Several polyhedra have rhombic faces, such as the rhombic dodecahedron and the trapezo-rhombic dodecahedron.

Some polyhedra with all rhombic faces

Isohedral polyhedra		Not isohedral polyhedra
Identical rhombi	Identical golden rhombi		Two types of rhombi	Three types of rhombi
Rhombic dodecahedron	Rhombic triacontahedron	Rhombic icosahedron	Rhombic enneacontahedron	Rhombohedron

Литература

• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. 
• Љиљана Петрушевски - Полиедри
• Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
• Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ур.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. стр. 43—70. ISBN 978-94-010-4398-4. 
• Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Архивирано на сајту Wayback Machine (3. август 2016))
• Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
• Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
• Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
• Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
• Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
• Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067. 
• Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678 
• Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7 
• Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093 . doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г. 
• Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. стр. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6. 
• Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289 ; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), стр. 80—86, doi:10.1145/800061.808735 
• Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd изд.), Oxford: Clarendon Press, MR 0124167 .
• Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049 .
• Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ур.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, стр. 461—488, CiteSeerX 10.1.1.102.755 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21 .
• Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037 .
• Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ур.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, стр. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15 .
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208 .
• Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688 
• de Villiers, Michael, "Equiangular cyclic and equilateral circumscribed polygons", Mathematical Gazette 95, March 2011, 102-107.

Спољашње везе

• Parallelogram and Rhombus - Animated course (Construction, Circumference, Area)
• Rhombus definition, Math Open Reference
• Rhombus area, Math Open Reference