Алгоритам множења
Алгоритам множења је алгоритам (или метода) за множење два броја. У зависности од величине бројева, могу се користити различити алгоритми. Ефикасни алгоритми множења постоје још од појаве децималног система.
Метод мреже (грид метод)[уреди | уреди извор]
Метод мреже или метод кутије је уводни метод за множење вишецифрених бројева, и често се учи у основној школи. То је стандардни део националног плана и програма за математику у основним школама у Енглеској и Велсу од касних 1990-их година. Оба фактора (броја) су подељена на стотине, десетице и јединице, и производи делова се затим рачунају експлицитно у релативно једноставној фази множења, пре него што се на крају саберу да би се добио коначни резултат.[1]
Пример је множење 34x13, може се израчунати коришћењем мреже:
300 40 90 + 12 ———— 442
× 30 4 10 300 40 3 90 12
а затим се сабирају да би се добило 442, било у једној суми, или кроз формирање ред по ред збирова (300 + 40) + (90 + 12) = 340 + 102 = 442.
Овај приступ рачунања (мада не обавезно са експлицитним аранжманом мреже) је такође познат и као алгоритам делимичних производа. Његова суштина је одвојено рачунање једноставних множења, при чему се сабирање оставља за крајњу фазу.
Метод мреже се у принципу може применити на факторе било којих величина, иако број потпроизвода може постати јако велики како се повећава број цифара. Свакако представља корисни експлицитни метод као увод за идеју множења вишецифрених бројева; и у доба када се већина рачунања врши помоћу дигитрона, ово може бити једини алгоритам множења који ће ученицима икад бити потребан.
Дуго множење[уреди | уреди извор]
Ако се користи позициони систем бројева, природан начин множења који се учи у школама је метод дугог множења, некад називан и стандардним алгоритмом: помножити множеник сваком цифром множиоца и онда их сабрати све исправно. Овај начин захтева меморисање таблице множења за једноцифрене бројеве.
Ово је уобичајени алгоритам за множење већих бројева на папиру, чија је основа 10. Компјутери су на почетку користили сличан алгоритам померања и додавања бројева чија је основа 2, али модерни процесори имају оптимизована кола за брза множења користећи ефикасније алгоритме, по цени сложеније хардверске реализације. Особа која ради дуго множење на папиру ће записати све производе и затим их сабрати, али особа која користи абакус ће сабирати производе након сваког рачунања.
Пример[уреди | уреди извор]
Овај пример користи дуго множење да би се помножио 23 958 233 (множеник) са 5830 (множилац), и добија се 139 676 498 390 (резултат).
23958233
× 5830
———————————————
00000000 ( = 23,958,233 × 0)
71874699 ( = 23,958,233 × 30)
191665864 ( = 23,958,233 × 800)
+ 119791165 ( = 23,958,233 × 5,000)
———————————————
139676498390 ( = 139,676,498,390 )
Испод се налази псеудокод који описује процес множења наведен изнад. У њој се налази само један ред који одржава суму која ће на крају бити финални резултат. Обратити пажњу да се оператор += користи да означи суму постојеће вредности и сачува операцију, као у програмским језицима C и Јава.
multiply(a[1..p], b[1..q], base) // Operandi na desnoj poziciji sadrže cifru 1
product = [1..p+q] //Dodeliti prostor za rezultat
for b_i = 1 to q // za sve cifre u b
carry = 0
for a_i = 1 to p //za sve cifre u a
product[a_i + b_i - 1] += carry + a[ai] * b[bi]
carry = product[ai + bi - 1] / base
product[a_i + b_i - 1] = product[ai + bi - 1] mod base
product[b_i + p] += carry // poslednja cifra dolazi iz konačnog prenosa
return product
Множење решетком[уреди | уреди извор]
Множење решетком или ситом је алгоритамски еквивалент дугог множења. Захтева пипрему решетке, тј мреже нацртане на папиру која води рачунање и раздваја множења од сабирања. Први пут је коришћен у Европи 1202. године у Фибоначијевој "Либер Абаци". Леонардо описује ову операцију као менталну, користећи и десну и леву руку како би преносио прелазна рачунања. Матракци Насух је представио 6 различитих варијанти ове методе у књизи из 16.века "Умдет-ул Хисаб". Коришћена је у Ендерун школама широм Отоманског царства. Напијерове шипке или кости су такође користиле ове методе.
Као што је приказано у примеру, множеник и множилац су написани изнад и десно од решетке или сита. Током фазе множења, решетка се попуњава двоцифреним производима одговарајућих цифара које означавају сваки ред и колону. Десетице иду у горњи леви угао.
Током фазе сабирања, решетка се сабира на дијагоналама. На крају, ако је неопходна фаза померања, решење приказано на левим и доњим странама решетке се конвертује у нормалну форму преносом цифара десетица као у алгоритму дугог множења.
Пример[уреди | уреди извор]
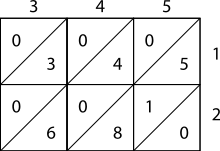

Слика на десној страни показује како израчунати 345 × 12 користећи множење решетком. Као сложенији пример можемо размотрити слику испод која приказује множење 23 958 233 са 5830, резултат је 139 676 498 390. Обратити пажњу да је 23 958 233 на врху решетке а 5830 је са десне стране. Производи попуњавају решетку или суме тих производа (на дијагонали) су дуж левих и доњих страна. Затим су те суме израчунате, као што је приказано.
2 3 9 5 8 2 3 3
+---+---+---+---+---+---+---+---+-
|1 /|1 /|4 /|2 /|4 /|1 /|1 /|1 /|
| / | / | / | / | / | / | / | / | 5
01|/ 0|/ 5|/ 5|/ 5|/ 0|/ 0|/ 5|/ 5|
+---+---+---+---+---+---+---+---+-
|1 /|2 /|7 /|4 /|6 /|1 /|2 /|2 /|
| / | / | / | / | / | / | / | / | 8
02|/ 6|/ 4|/ 2|/ 0|/ 4|/ 6|/ 4|/ 4|
+---+---+---+---+---+---+---+---+-
|0 /|0 /|2 /|1 /|2 /|0 /|0 /|0 /|
| / | / | / | / | / | / | / | / | 3
17|/ 6|/ 9|/ 7|/ 5|/ 4|/ 6|/ 9|/ 9|
+---+---+---+---+---+---+---+---+-
|0 /|0 /|0 /|0 /|0 /|0 /|0 /|0 /|
| / | / | / | / | / | / | / | / | 0
24|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|
+---+---+---+---+---+---+---+---+-
26 15 13 18 17 13 09 00
|
01 002 0017 00024 000026 0000015 00000013 000000018 0000000017 00000000013 000000000009 0000000000000 ————————————— 139676498390 |
| = 139,676,498,390 |
Бинарно множење[уреди | уреди извор]
За бројеве чија је основа 2, дуго множење се своди на тривијалну операцију. За сваки бит јединицу у мултиплиер, померити мултиплицанд за одговарајући износ, а затим сабрати померене вредности. У зависности од архитектуре процесора рачунара и избора мултиплиера, мозе бити брже кодирати овај алгоритам коиристећи хардверско померање и сабирање битова него зависити од инструкција за множење, када је мултиплиер фиксиран и број сабирања је мали.
Овај алгоритам се назива још и сељачко множење, јер је био у широкој употреби међу онима који нису били школовани и самим тим нису упамтили таблицу множења које захтева дуго множење. Овај алгоритам се такође користио и у древном Египту.
На папиру, запишите у једној колони бројеве које добијете када више пута преполовите мултиплиер, игноришући остатак. у колони поред њега у више наврата удвостручити мултиплицанд. Прецртати сваки ред у коме је последња цифра првог броја парна, и додајте преостале бројеве у другу колону како би се добио резултат.
Главне предности ове методе су те да може да се научи брзо, меморисање није потребно, и може се извести коришћењем токена као сто су чипови за покер ако папир и оловка нису доступни. Међутим, има више корака од дугог множења тако да може да буде незграпно када су у питању велики бројеви.
Примери[уреди | уреди извор]
Овај пример користи бинарно множење да помножи 11 са 3, при чему се добија резултат 33.
Decimalno: Binarno: 11 3 1011 11 5 6 101 110 2121011001 24 1 11000 —— —————— 33 100001
Експлицитни опис корака: 11 и 3 су написани на врху. 11 је преполовљено на 5.5 а 3 је удвостручено на 6. Фракциони део, тј. део иза децимале се одбацује. 5 је преполовљено на 2.5 а 6 је дуплирано на 12. Децимални део се одбацује.
Број у левој колони је паран, тако да се део у десној колони одбацује. 2 се полови а 12 се дуплира.
Све непрецртане вредности се саберу: 3+6+24=33.
Овај метод ради јер је множење дистрибутивна операција, тако да
Компликованији пример, са коришћењем претходно наведених цифара (23 958 233 и 5 830):
Decimal: Binary: 583023958233101101100011010110110110010010110110012915 47916466 101101100011 10110110110010010110110010 1457 95832932 10110110001 101101101100100101101100100 72819166586410110110001011011011001001011011001000364383331728101101100101101101100100101101100100001827666634561011011010110110110010010110110010000091 1533326912 1011011 1011011011001001011011001000000 45 3066653824 101101 10110110110010010110110010000000 2261333076481011010110110110010010110110010000000011 12266615296 1011 1011011011001001011011001000000000 5 24533230592 101 10110110110010010110110010000000000 249066461184101011011011001001011011001000000000001 98132922368 1 1011011011001001011011001000000000000 ———————————— 1022143253354344244353353243222210110 (before carry) 139676498390 10000010000101010111100011100111010110
Остали алгоритми множења[уреди | уреди извор]
- Померање и сабирање
- Множење "qуартер сqуаре"
- Алгоритам за множење бројева близу целог броја
- Гаусов комплексни алгоритам множења
- Карацубин алгоритам множења
- Тоом-Цоок алгоритам множења
- Фуријеове трансформације
Види још[уреди | уреди извор]
- Бинарни множеник
- Алгоритам дељења
- Логаритам
- Логаритмар
Референце[уреди | уреди извор]
- ^ Гарy Еасон, Бацк то сцхоол фор парентс, ББЦ Неwс, 13 Фебруарy 2000
Роб Еастаwаy, Wхy парентс цан'т до матхс тодаy Архивирано на сајту Wayback Machine (4. март 2016), ББЦ Неwс, 10 Септембер 2010
Спољашње везе[уреди | уреди извор]
- "ББЦ - бацк то сцхоол фор парентс"
- "ББЦ - Wхy парентс цан'т до матх тодаy" Архивирано на сајту Wayback Machine (4. март 2016)
- Новел Метходс оф Интегер Мултиплицатион анд Дивисион
- Qуартер Таблес Ревиситед: Еарлиер Таблес, Дивисион оф Лабор ин Табле Цонструцтион, анд Латер Имплементатионс ин Аналог Цомпутерс
- Фаст Фоуриер трансформатионс: а туториал ревиеw анд а стате оф тхе арт
- Фастер интегер мултиплицатионс

