Елиптичка крива

У математици, елиптичка крива је глатка, пројективна алгебарска крива рода један, на којој је означена тачка O. Елиптичка крива је у ствари Абелов варијетет – то јест има алгебарски дефинисано множење у односу на које је Абелова група – а O служи као неутрал. Често се сама крива, без означеног O назива елиптичком кривом.
Свака елиптичка крива може да се запише као алгебарска крива дефинисана једначином облика
- .
Оваква једначина назива се Вајерштрасовом једначином. Крива је несингуларна ако њен график нема сингуларних тачака или самопресека. (Када је карактеристика поља коефицијената једнака 2 или 3, горња једначина није довољно општа да укључи све несингуларне кубне криве.) Тачка O је у ствари тачка у бесконачности на пројективној равни.
Ако је y2 = P(x), где је P било који полином степена три од x без поновљених коренова (односно, ако је дискриминанта полинома P не-нула), онда се добија несингуларна планарна крива рода један, која је стога такође и елиптичка крива. Ако је P степена четири и нема поновљених фактора, ова једначина опет описује криву рода један; међутим она нема природно изабран неутрал. Општије, свака алгебарска крива рода један, на пример добијена пресеком две тродимензионе квадратне површине, се назива елиптичком кривом, под условом да има барем једну рационалну тачку.
Елиптичке криве су посебно важне у теорији бројева, и област су већег дела савременог проучавања; на пример, кориштене су у доказу Велике Фермаове теореме до ког је (уз помоћ Ричарда Тејлора) дошао Ендру Вајлс. Свакој холоморфној модуларној форми тежине 2 и одговарајућег небентипуса одговара елиптичка крива; кључни резултат Вајлсовог и Тејлоровог доказа и истраживања која су уследила јесте да важи и обрнуто, односно да је свака елиптичка крива модуларна.
Елиптичке криве такође имају примене у криптографији (види чланак: криптографија елиптичких кривих) и факторизацији целих бројева.
Елиптичка крива није елипса, нити је елипса елиптичка крива. Видети елиптички интеграл за порекло израза.
Елиптичке криве над реалним бројевима[уреди | уреди извор]
Иако је формална дефиниција елиптичке криве прилично техничка по природи и захтева познавање алгебарске геометрије, могуће је описати нека својства елиптичких кривих над реалним бројевима коришћењем само средњошколске алгебре и геометрије.
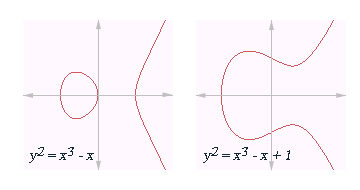
У овом контексту, елиптичка крива је планарна крива дефинисана једначином облика
где су a и b реални бројеви. Овај тип једначине се назива Вајерштрасовом једначином.
Дефиниција елиптичке криве такође захтева да крива буде несингуларна. Геометријски, ово значи да график не сме да има сингуларних тачака или самопресека. Алгебарски, ово подразумева израчунавање дискриминанте
Крива је несингуларна ако је њена дискриминанта различита од нуле. (Иако фактор −16 изгледа небитан овде, испоставља се да је он згодан у напреднијим проучавањима елиптичких кривих.)
График несингуларне криве има две компоненте ако је њена дискриминанта позитивна а једну компоненту ако је дискриминанта негативна. На пример, у горе приказаним графицима, дискриминанта је у првом случају 64, док је у другом случају −368.
Закон групе[уреди | уреди извор]
Додавањем тачке у бесконачности, добија се пројективна верзија ове криве. Ако су P и Q две тачке на кривој, онда јединствено може да се опише трећа тачка која је пресек криве и праве која пролази кроз P и Q. Ако је права тангента на криву у некој тачки, онда се та тачка броји двапут; ако је права паралелна y-оси, онда се трећа тачка дефинише као тачка у бесконачности. Тачно један од ових услова важи за било који пар тачака на елиптичкој кривој.
Тада је могуће увести операцију над групом, "+", над кривом, која има следећа својства: тачка у бесконачности се узима да је 0, неутрал групе; ако права пресеца криву у тачкама P, Q и R, онда се захтева да је P + Q + R = 0 У овој групи. Може се показати да ово претвара криву у Абелову групу, па стога и у Абелов варијетет. Такође се може показати да скуп K-рационалних тачака (укључујући тачку у бесконачности) формира подгрупу ове групе. Ако се крива означава као E, онда се ова подгрупа обично означава као E(K).
Горња група може да се опише алгебарски као и геометријски. За дату криву y2 = x3 − px − q над пољем K (за чију карактеристику важи претпоставка да није ни 2 нити 3), и тачке P = (xP, yP) и Q = (xQ, yQ) на кривој, нека важи претпоставка xP ≠ xQ. Нека је s = (yP − yQ)/(xP − xQ); како је K поље, s је добро дефинисано. Тада може да се дефинише R = P + Q = (xR, yR) као
Ако је xP = xQ, онда постоје два случаја: ако је yP = −yQ, укључујући случај када је yP = yQ = 0, тада је сума дефинисана као 0; дакле, инверз сваке тачке на кривој се налази њеном рефлексијом по x-оси. Ако је yP = yQ ≠ 0, онда је R = P + P = 2P = (xR, - yR) дато преко
Спољашње везе[уреди | уреди извор]
- Математички атлас: 14H52 Елиптичке криве
- Ерик В. Вајсштајн, Елиптичке криве на MathWorld.
- Аритметика елиптичких кривих Архивирано на сајту Wayback Machine (8. новембар 2009) на PlanetMath
- Матлаб код за исцртавање графика имплицитних функција Архивирано на сајту Wayback Machine (17. март 2006) - може да се користи за цртање елиптичких кривих.
- Интерактивни увод у елиптичке криве и криптографију елиптичких кривих[мртва веза]
Овај чланак укључује материјал са одреднице Изогенија на сајту PlanetMath, која је лиценцирана под ГЛСД.









