Алгебра

	Овај чланак или један његов део нема никакве независне и поуздане изворе. Помозите да се овај чланак побољша тако што ћете унети одговарајуће референце. Текст који не садржи референце може бити доведен у питање, а потом и уклоњен.

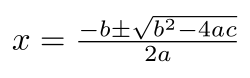
Алгебра (Algebra), арап. al-gabr, у ствари „узглобљавање (поломљених) делова“, успостављање равнотеже, облик једначине.

Генеза назива води до књиге арапског математичара Ал Хорезмија Хисаб ал џабр вал мукабала што се у слободнијем преводу може бити Књига о свођењу и двоструком одузимању. Поступак се прво односио на уређивање леве и десне стране код једначина али је касније, развојем математике, значајно проширен.

Изворно се под „алгебром“ подразумевала теорија „алгебарских“ једначина, у којима су помоћу „алгебарских“ рачунских операција (сабирање, одузимање, множење, дељење итд.) повезане познате и непознате величине. Данас овај појам означава и општију теорију математичких структура, у којој се посебно истражују структурне једнакости између тако различито усмерених области као што су теорија бројева, геометрија или алгебра у традиционалном смислу.

Важне алгебарске структуре су, рецимо, групе, прстени, тела и асоцијације. Све творевине које показују неку одређену структуру називају се „модели“ ове структуре. Резултати на које се смера истраживањима апстрактних структура покаткад важе и за њихове моделе.

Надовезујући се на Mathematical Analysis of Logic (1847.) Џорџ Була, алгебарска истраживања су постала значајна и за формалну логику. Важну улогу ту играју посебно „буловске асоцијације“ или „буловске алгебре“. Поред алгебарских структура, говори се још и ο „структурама уређења“ и „тополошким структурама“.

Класификација

Алгебра може грубо да се подели у следеће категорије:

• Елементарна алгебра, у којој се проучавају својства операција над реалним бројевима, као и правила која се тичу математичких израза и једначина. У ову сврху се користе словни симболи за представљање константи и променљивих.
• Апстрактна алгебра, која се назива још и модерном алгебром, у којој се аксиоматски дефинишу и проучавају алгебарске структуре попут група, прстена и поља.
• Линеарна алгебра, у којој се проучавају специфична својства векторских простора (укључујући матрице).
• Универзална алгебра, у којој се проучавају својства заједничка свим алгебарским структурама.
• Алгебарска теорија бројева, у којој се сњвојства бројева проучавају помоћу алгебарских система. Теорија бројева је инспирисала значајан део развоја апстракције у алгебри.
• Алгебарска геометрија, у којој се геометријским проблемима прилази са алгебарског аспекта.
• Алгебарска комбинаторика, у којој се користе апстрактни алгебарски методи за проучавање комбинаторних питања.

У неким областима напредног изучавања, аксиоматски алгебарски системи као што су групе, прстени, поља и алгебре над пољима, се проучавају у присуству геометријске структуре (метрика или топологија) која је у складу са том алгебарском структуром. Овај списак укључује разне области функционалне анализе:

• Нормирани линеарни простори
• Банахови простори
• Хилбертови простори
• Банахове алгебре
• Нормиране алгебре
• Тополошке алгебре
• Тополошке групе

Спољашње везе

Викимедијина остава има још мултимедијалних датотека везаних за: Алгебра