Метода контурних струја

Метода контурних струја је метода за решавање електричних кола у равни чиме се добијају струје и индиректно и напони у било ком делу електричног кола. Метода контурних струја користи други Кирхофов закон да би добила скуп једначина које је сигурно могуће решити уколико електрично коло може да се реши.^[1] Метода контурних струја је углавном лакша за коришћење уколико је електрично коло у равни.^[2]

Контурне струје[уреди | уреди извор]

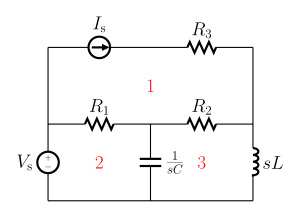
Метода контурних струја се користи тако што се прво произвољно доделе контурне струје у контурама. Контуре су затворени путеви унутар електричног кола који не садрже друге контуре у себи. На слици су означене контуре са 1, 2 и 3.^[3]

Контурна струја је струја која се креће око те контуре и једначине се решавају у односу на њих. Контурна струја не мора да буде иста као и стварна струја кроз тај део кола, али се стварне струје лако налазе из контурних. Пракса је да се све контурне струје поставе тако да су оријентисане у истом смеру. Ово смањује број грешака при писању једначина. Конвенција је да су све контурне струје оријентисане у смеру казаљке на сату.

Решавање контурних струја уместо директна примена Кирхофових закона може много да смањи број потребних израчунавања. То се дешава зато што постоји мање контурних струја него што има стварних струја у гранама електричног кола. У слици 2 нпр., има 6 струја грана у колу, али само 3 контурне струје.

Постављање једначина[уреди | уреди извор]

Свака контура производи једну једначину. Ове једначине су сума падова напона у комплетној контури контурне струје.^[4]

Уколико је напонски извор присутан унутар контурне струје, напон извора се или додаје или одузима, у зависности од тога да ли је пад напона или повећање напона у смеру контурне струје. За струјни извор који се не налази између две контуре, контурна струје ће добити његову позитивну или негативну вредност у зависности од тога да ли је контурна струја истог или супротног смера у односу на струјни извор. Следи претходно приказано електрично коло на слици 2, са свим једначинама потребним за решавање свих струја у електричном колу.

${\begin{cases}{\text{Mesh 1: }}I_{1}=I_{s}\\{\text{Mesh 2: }}-V_{s}+R_{1}(I_{2}-I_{1})+{\frac {1}{sc}}(I_{2}-I_{3})=0\\{\text{Mesh 3: }}{\frac {1}{sc}}(I_{3}-I_{2})+R_{2}(I_{3}-I_{1})+LsI_{3}=0\\\end{cases}}\,$

Када се једначине напишу, систем линеарних једначина може да се реши коришћењем било које методе за решавање линеарних једначина.

Специјални случај[уреди | уреди извор]

Постоје два специјална случаја у контурним струјама: струје које садрже суперконтуру и струје које садрже зависне изворе.

Суперконтура[уреди | уреди извор]

Суперконтура настаје када се струјни извор налази између две контуре. Електрично коло се прво посматра као да струјни извор не постоји. Ово доводи до једначине која садржи две контурне струје. Када се ова једначина напише, потребна је још једна једначина која говори о односу те две контурне струје са струјним извором. Ово ће бити једначина где је струјни извор једнак једној контурној струји минус другој. Следи једноставан пример за рад са суперконтурама.

${\begin{cases}{\text{Mesh 1, 2: }}-V_{s}+R_{1}I_{1}+R_{2}I_{2}=0\\{\text{Current source: }}I_{s}=I_{2}-I_{1}\end{cases}}\,$

Зависни извори[уреди | уреди извор]

Зависни извор је струјни извор или напонски извор који зависи од напона или струје или друге компоненте унутар електричног кола. Када се зависни извор налази унутар контуре, потребно га је посматрати као независни извор. Када се формира једначина контуре, зависни извор је потребан. Ова једначина одређује однос зависног извора у односу на напон или струју од чије вредности зависи вредност извора. Следи пример зависног извора.

${\begin{cases}{\text{Mesh 1: }}-V_{s}+R_{1}I_{1}+R_{3}(I_{1}-I_{2})=0\\{\text{Mesh 2: }}R_{2}I_{2}+3I_{x}+R_{3}(I_{2}-I_{1})=0\\{\text{Dependent variable: }}I_{x}=I_{1}-I_{2}\end{cases}}\,$

Види још[уреди | уреди извор]

Референце[уреди | уреди извор]

^ Hayt, William H., & Kemmerly, Jack E. (1993). Engineering Circuit Analysis (5th ed.), New York: McGraw Hill.
^ Nilsson, James W., & Riedel, Susan A. (2002). Introductory Circuits for Electrical and Computer Engineering. New Jersey: Prentice Hall.
^ Lueg, Russell E., & Reinhard, Erwin A. (1972). Basic Electronics for Engineers and Scientists (2nd ed.). New York: International Textbook Company.
^ Puckett, Russell E., & Romanowitz, Harry A. (1976). Introduction to Electronics (2nd ed.). San Francisco: John Wiley and Sons, Inc.

Спољашње везе[уреди | уреди извор]

[Hayt-1] Hayt, William H., & Kemmerly, Jack E. (1993). Engineering Circuit Analysis (5th ed.), New York: McGraw Hill.

[Nilsson-2] Nilsson, James W., & Riedel, Susan A. (2002). Introductory Circuits for Electrical and Computer Engineering. New Jersey: Prentice Hall.

[Russell-3] Lueg, Russell E., & Reinhard, Erwin A. (1972). Basic Electronics for Engineers and Scientists (2nd ed.). New York: International Textbook Company.

[Romanowitz-4] Puckett, Russell E., & Romanowitz, Harry A. (1976). Introduction to Electronics (2nd ed.). San Francisco: John Wiley and Sons, Inc.

[1]

[2]

[3]

[4]