Систем линеарних једначина

У математици и линеарној алгебри, систем линеарних једначина је скуп линеарних једначина, као што је
Стандардни проблем је да се утврди да ли постоји скуп вредности за непознате , који задовољава све једначине истовремено, и да се нађе такав скуп уколико постоји. Постојање скупа решења зависи од једначина, али и од доступних вредности (да ли се ради о целим бројевима, реалним бројевима, и слично). Систем из горњег примера има јединствено решење:
Историја[уреди | уреди извор]
Задаци који се своде на састављање и решавање система једначина са две или више непознатих, били су познати још у вавилонским и египатским текстовима из 2. миленијума пре н.е., као и у радовима старогрчких, индијских и кинеских математичара.[1]
Најпознатија старокинеска збирка задатака под називом „Девет поглавља вештине рачунања.”, чији је аутор непознат, настала је у време Хан династије (из период од 206. п. н. е. до 220. н.е), а њено седмо и осмо поглавље се баве системима линеарних једначина.[1]
Један од задатка из најстарије кинеске математичке збирке задатака гласи: у кавезу се налазе фазани и зечеви; све те животиње имају укупно 35 глава и 94 ноге. Треба наћи број фазана и број зечева. Решење задатка гласи: ако би у кавезу били само фазани, што је лажна претпоставка, онда би број ногу износио 70, а не 94. Према томе, вишак од 24 ноге припада зечевима – по два свакоме. Тада је јасно да је зечева било 24 : 2 = 12, а фазана 35 - 12 = 23.[2]
Карактеристично је да су у тим почетним збиркама системи једначина увек били са једнаким бројем једначина и непознатих. У седмом поглављу, које носи назив „Вишак – мањак” , изложена су две методе за решавање задатака, који се своде на систем две линеарне једначине са две непознате. Познавали су методу детерминанти, која се данас назива Крамеровим правилом.[1]
Једначине су се решавале шематски. За њихово решавање су дата кратка правила, при чему се све излаже речима. Упутства су била формулисана тако да је сваки од коефицијената уз непознате носио свој назив, а поступак је развијен полазећи од кинеске табле за рачунања. Коефицијенти једначине постављени су у виду таблице, као посебна врста абакуса. При поновљеним операцијама на тој рачунаљци, јасно се види да са коефицијентима треба поступати по истом правилу, да би се нашло решење система једначина.[2]
Други начин који су примењивали је била оно која се данас назива Гаусова метода елиминације, а тада се звала метода две лажне претпоставке и примењивана је нарочито у средњем веку, па све до 18. века.[3]
У 12. веку техника лажних претпоставки пренета је из арапске у европску математичку литературу, где је била позната под латинским називом лат. regula duorum falsorum – правило двеју грешака.[4]
Систем две линеарне једначине са две непознате[уреди | уреди извор]
Посебан случај система линеарних једначина је скуп од две линеарне једначине са две непознате, односно променљиве, код којих су решења тих непознатих иста. Општи облик система две једначине са две непознате је следећи:
где су x, y скуп непознатих вредности, а коефицијенти познати параметри, у облику реалних бројева. Коефицијенте се називају задати коефицијенти, док се коефицијенти називају слободни коефицијенти. Решење овог система би био сваки уређени пар бројева , за који важи да је:
За систем од две линеарне једначине с две непознате постоје три могућности:
- систем је одређен ако постоји само једно решење, односно један уређени пар , који задовољава систем једначина
- систем је неодређен ако постоји бесконачно много решења, односно уређених парова који задовољавају систем једначина. Када систем са две једначине и две промељниве има више од једног решења, онда је једна променељива слободна.
- Пример:
- Следећи систем једначина има бесконачно много решења:
- и оно се изражава у облику где се за променљиву x каже да је слободна, док је променљива у везана.
- систем је немогућ или контрадикторан, када не постоји ниједано решење за задати систем једначина.
- Пример:
- Следећи систем једначина је немогућ, јер не постоје бројеви који би могли да је задовоље:
Еквивалентност система линеарних једначина[уреди | уреди извор]
Два система једначина су еквивалентна ако је свако решење једног од њих уједно решење и другог, или ако оба система немају решење.
Систем еквивалентан систему, чија бар једна једначина нема решење, такође нема решење.
У случају да задати систем није представљен у општем облику, он се може свести на општи облик еквивалентним трансформацијама.
Трансформације које систем линеарних једначина преводе у њему еквивалентан систем су:
- замена места двеју једначина
- множење свих коефицијената једне једначине константом
- додавање коефицијената једне једначине одговарајућим коефицијентима друге једначине
Ако једначину система заменимо њој еквивалентном, добијамо нови систем еквивалентан полазном. Ако у једначини датог система заменимо једну од непознатих изразом који је једнак тој непознатој на основу друге једначине, добијамо нови систем који је еквивалентан полазном систему. Ако једну једначину датог система заменимо једначином која је збир или разлика једначина датог система, добијамо нови систем који је еквивалентан полазном систему.
Пример:
Ако се у полазном систему једначина
друга једначина замени збиром прве и друге једначине:
и променљива y изрази преко променљиве x у првој једначини, а друга једначина подели са 2:
те добијена вредност за x из друге једначине замени у првој једначини, добијени систем једначина је еквивалентан почетном систему:
Ради прегледности и лакшег решавања исте непознате се обично пишу једна испод друге.
Методе решавања система две линеарне једначине[уреди | уреди извор]
Решити систем једначина значи одредити решење или решења тог система или утврдити да тај систем нема решење. Под решавањем система линеарних једначина с две непознате подразумева се низ посту- пака којим се еквивалентним трансформацијама систем преводи у систем чије се решење непосредно одређује. Постоји више метода за решавања система линеарних једначина и све оне доводе до истог решења, а за решавање се бира она метода која се чини најпогоднија за постављени систем, односно да се добије еквивалентан систем у најједноставнијем облику.
Метода замене[уреди | уреди извор]
Поступак се састоји у томе да се на основу једне од две задате једначине једна непозната изрази преко друге непознате (x преко y или y преко x), а затим се тако изражена непозната замени у другој једначини, чиме се проблем своди на решавање једне једначине са једном непознатом. Избор о томе коју променљиву изразити преко друге је слободан, тако да се бира оно што је у датом случају погодније.
Методу замене је набоље примењивати када је бар један коефицијент уз неку од непознатих једнак 1 или -1, јер се тада применом правила о додавању једна непозната лако изражава преко друге.
Пример 1:
Решавање:
Непозната x се у првој једначини изрази преко непознате y:
и замени у другој једначини:
односно, множењем целе једначине са -1:
што се своди на:
Заменом вредности за , у једначини у којој је x изражено преко y добија се :
Закључујемо да је постављени систем једначина одређен и да његово решење представља уређени пар с вредностима .
Провера:
Провера тачности решења се врши заменом израчунатог решења, односно уређеног пара израчунатих вредности у почетне једначине:
Пример 2:
Решавање: Непозната y се у првој једначини изрази преко непознате x:
и замени у другој једначини:
што се своди на:
и значи да је систем једначина немогућ, односно да нема решења.
Метода супротних коефицијената[уреди | уреди извор]
За методу супротних коефицијената кључна је примена правила које гласи: ако једну од једначина система заменимо збиром или разликом једначина тог система, добијамо систем еквивалентан полазном систему. Поступак се састоји у множењу једначине одговарајућим бројем, при чему се коефицијенти испред једне од непознатих у обе једначине претварају у исте бројеве.
Ако су знаци испред те непознате супротни, сабирањем једначина се та непозната елиминише, а ако су знаци исти, да би се једна непозната елиминисала, једначине се одузимају. Елминисањем једне од непознатих, проблем се поново своди на једну једначину са једном непознатом. Елиминисана непозната се касније може израчунати заменом прве израчунате непознате у било којој од постављених једначина.
Методу супротних коефицијената је најзгодније примењивати када су коефицијенти уз исту непознату у обе једначине система међусобно супротни бројеви или међусобно једнаки бројеви.
Пример 1:
Решавање:
Да би се добили супротни коефицијенти, најлакше је помножити прву једначину са -2:
Сабирањем једначина добијамо:
множењем са -1:
се своди на:
Да би се добила вредност за x, довољно је заменити вредност за y, у било којој од две једначине. На пример, заменом у првој једначини:
Закључујемо да је постављени систем једначина одређен и да његово решење представља уређени пар с вредностима .
Графичка метода[уреди | уреди извор]
Поступак се састоји у графичком представљању сваке од задатих једначина. С обзиром да су непознате линеарно зависне, њихова графичка представа је линеарна функција, која има облик праве линије у истој равни, а за конструисање права довољно је израчунати вредности непознатих (x, y) у само две тачке, као на пример, у тачкама x = 0 и y = 0. Графичко решавање система се састоји у тражењу на графику уређеног пара , у коме се праве секу.
Две праве једне равни могу се наћи у једном од три различита међусобна односа:
- праве се секу, односно имају само једну заједничку тачку. У том случају систем је одређен и постоји јединствено решење
- праве су паралелне, али се не поклапају, растојање између њих је увек исто и немају заједничких тачака. У том случају се ради о немогућем систему, односно решење за постављени систем не постоји
- праве се поклапају, односно имају бесконачно много заједничких тачака. То значи да систем једначина има бесконачно много решења и да је систем неодређен
Пример 1:
Решавање:
У првој једначини се y изражава преко x на следећи начин:
Да би се нацртала функција, може се користити табела, на пример за вредности x = 0 и x = 7:
| x | 0 | 7 |
|---|---|---|
| y | 4 | 3 |
У другој једначини се y изражава преко x на следећи начин:
Множењем са -1 добија се:
Да би се нацртала функција може се користити табела за вредности x = 0 и x = 5:
| x | 0 | 5 |
|---|---|---|
| y | -11 | -1 |
Решење једначина се добија у пресеку правих, која се налази у тачци (7,3), односно систем има јединствено решење:

Пример 2:
Решавање:
Из прве једначине се изрази y преко x:
Затим се израчунају вредности y за најмање две вредности x зашта се може користити табела:
| x | 0 | 2 |
|---|---|---|
| y | -4 | 0 |
Из друге једначине се изрази y преко x:
Затим се израчунају вредности y за најмање две вредности x зашта се може користити табела:
| x | 0 | -3 |
|---|---|---|
| y | 6 | 0 |
Цртањем функција видимо да су праве паралелне, нема пресека, задати систем једначина нема решење
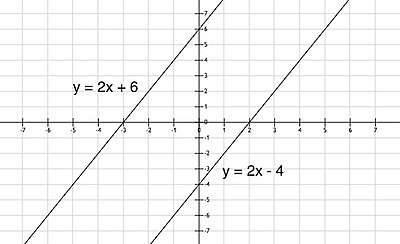
Пример 3:
Решавање:
Поређењем једначина може се уочити да су једначине еквиваленте, односно да се друга једначина добија множењем прве једначине са 4, односно обе једначине се могу представити истом функцијом:
Да би се нацртала функција потребно пронаћи најмање две тачке, зашта користимо табелу:
| x | 0 | 4 |
|---|---|---|
| y | -4 | 0 |

Примена система две линеарне једначине са две непознате[уреди | уреди извор]
Системи линеарних једначина се јављају при решавању различитих проблема. Примери:
Пример 1:
Збир два броја је за 2 већи од троструке вредности мањег од та два броја, а петострука вредност мањег је једнака двострукој вредности већег. О којим бројевима је реч?
Поставка система једначина:
Нека је x мањи од два тражена броја, а y већи. У том случају може се поставити следећи систем једначина:
Решавање:
Методом замене може се изразити вредност променљиве y преко променљиве x:
када се ова вредност замени у другој једначини добија се:
Заменом добијене вредности за x у еквивалентној једначини:
добија се:
Тражени бројеви су 4 и 10.
Провера:
Заменом добијених вредности за x и y, у првој и другој једначини се добија:
Оба израза су тачна.
Пример 2: Дуж истог пута равномерном брзином у истом смеру се крећу камион и иза њега аутомобил. У почетку растојање између ова два возила је износило 400 m. Након 40 секунди аутомобил је стигао камион. Тада је камион смањио своју брзину за трећину и након 20 секунди растојање између возила је износило 300 m, при чему је аутомобил био испред камиона. Одредити првобитне брзине којим су се кретали аутомобил и камион.
Поставка система једначина:
Нека је првобитна брзина камиона (изражена у ), а првобитна брзина аутомобила (такође изражена у ). У том случају могу се поставити једначине пређених путева, камиона и аутомобила, након првих 30 секунди и након наредних 20 секунди:
Решавање: Дељењем прве једначине са 40 и друге једначине са 20 систем се своди на:
Који се најлакше решава применом негативних коефицијента, односно одузимање друге једначине од прве:
односно
одакле се добија:
Заменом вредности у првој једначини добија се:
односно:
Брзина камиона износила је на почетку 15 , а аутомобила 25 .
Гаусова метода елиминације[уреди | уреди извор]
У систему од две линеарних једначине са две непознате:
Ако претпоставимо да је прва једначина се може помножити са бројем :
и сабере се са другом једначином добија се:
односно:
Добија се систем у коме треба посматрати неколико случајева случајева.
Ако је разлика , односно систем има јединствено решење које је одређено формулама:
- ,
Ако је разлика и бар један од бројева или различит од нуле, односно систем нема решења.
Ако је разлика разликују се три случаја:
- Ако је бар један од бројева различит од 0, систем има бесконачно много решења, односно неодређен је. Тако, на пример, ако је решење су сви парови реалиних бројева за које важи , где .
- ако је и бар један од бројева различит од нуле, систем нема решење.
- ако је систем је неодређен, има бесконачно много решења, сваки пар је решење система.
Општи облик система линеарних једначина[уреди | уреди извор]
Уопштено, систем са m линеарних једначина и n непознатих се записује на следећи начин
где су непознате, а бројеви су коефицијенти система.
Под решењем система линеарних једначина подразумевамо било који скуп од n бројева , који за идентички задовољавају систем.
Стављамо коефицијенте у матрицу на следећи начин:
Ако представимо сваку матрицу словом, ово постаје
где је A а m×n матрица, x је вектор колона са n чланова, а b је вектор колона са m чланова. Гаус-Жорданова елиминација се примењује на све ове системе, чак и ако су коефицијенти из неког произвољног поља.
Ако је поље бесконачно (као у случају реалних или комплексних бројева), могућа су само следећа три случаја (тачно један ће бити тачан) за сваки дати систем линеарних једначина:
- систем нема решења (систем је противречан)
- систем има тачно једно решење
- систем има бесконачно много решења
Одређен и неодређен системи имају заједнички назив, сагласни системи. Сагласни систем има најмање једно решење.
Ако су сви слободни чланови систем облика
се назива хомогеним системом линеарних једначина. Сваки хомоген систем је сагласан, јер има бар једно решење . Овакво решење се назива тривијално решење. Ако је хомоген систем систем одређен, онда он има само тривијално решење. Неодређени хомогени систем има и нетривијално решење.
Скуп свих решења система се назива нула простором матрице A. Посебно у светлу обиља горе наведених примена, неколико ефикаснијих алтернатива Гаус-Жордановој елиминацији је развијено за широк спектар специјалних случајева. Многи од ових побољшаних алгоритама су сложености O(n2) (види: нотација великог О). Неки од најуобичајенијих специјалних случајева су:
- За проблеме облика Ax' = b', где је A симетрична Теплицова матрица, може се користити Левинсонова рекурзија или нека од њених варијација. Једна од често окришћених варијација је Шурова рекурзија, која се користи у обради дигиталних сигнала.
- За проблеме облика Ax' = b', где је A сингуларна матрица, или готово сингуларна, матрица A се декомпонује у производ три матрица. Матрице са леве и десне стране су леви и десни сингуларни вектори. Матрица у средини је дијагонална матрица и садржи сингуларне вредности. Матрица тада може бити инвертовања простом заменом редоследа три компоненте, транспоновањем матрица сингуларних вектора, и узимањем реципрочне вредности дијагоналних елемената средишње матрице. Ако је било која од сингуларних вредности сувише близу нуле, и стога близу сингуларности, поставља се на нулу.
Примена система линеарних једначина[уреди | уреди извор]
Системи линеарних једначина спадају међу најстарије математичке проблеме, и имају многе примене, као што су обрада дигиталних сигнала, процене, предвиђање, као и линеарно програмирање, и апроксимација нелинеарних проблема у нумеричкој анализи. Постоји много начина да се реши систем линеарних једначина. Међутим, међу најефикаснијима су Гаусов поступак и декомпозиција Чолеског.
Референце[уреди | уреди извор]
- ^ а б в Бранковић 2015, стр. 4.
- ^ а б Бранковић 2015, стр. 5.
- ^ Бранковић 2015, стр. 7.
- ^ Бранковић 2015, стр. 9.
Литература[уреди | уреди извор]
- Ayres, Frank, Schaum's Outline of Modern Abstract Algebra, McGraw-Hill; 1st edition (June 1). 1965. ISBN 978-0-07-002655-1..
- Бранковић, Биљана (2015). Системи једначина у школи са освртом на проблемске задатке мастер рад (PDF). Београд: Математички факултет Универзитет у Београду. Приступљено 20. 5. 2018.
Види још[уреди | уреди извор]
Спољашње везе[уреди | уреди извор]
- Онлајн линеарни решавач
- Систем линеарних једначина са калкулатором
- Системи линеарних диференцијалних једначина
- (језик: француски) Решење линеарних система Архивирано на сајту Wayback Machine (15. септембар 2007)







































































































