Напонски разделник

У eлектроници, напонски разделник (такође познат и као потенцијални разделник) је линеарно коло које даје излазни напон (Vout) који представља део његовог улазног напона (Vin). Напонски разделник се односи на поделу напона између компоненте кола.
Пример напонског разделника се састоји од два отпорника или потенциометра у редној вези. Обично се користи за добијање референтног напона, или да је ниски напон сигнала пропорционалан напону који се мери, и такође се могу користити као сигнал Пригушник на ниским фреквенцијама. За једносмерну струју релативно ниских фреквенција, Напонски разделник може бити довољно прецизан ако су само отпорника, где се фреквентни одговор тражи преко широког опсега, (као што је у осцилоскоп сонде), напонски разделник може имати капацитивни елемент додат да омогући компензацију за капацитивност оптерећења. У пренос електричне енергије, капацитивни напонски разделник се користи за мерење високог напона.
Општи случај[уреди | уреди извор]
Напонски разделник наведен на терен је створена спајањем два електрична импеданса у серији, као што је приказано на слици 1. Улазни напон се примењује преко серије импеданси Z1 and Z2 и излазни напон је преко Z2. Z1 and Z2 може да се састоји од било које комбинације елемената, као што су отпорник, индуктор и кондензатор. Примена Омов закону, однос између улазног напона, Vin и излазног напона, Vout, могу се наћи:
Доказ: :
Функција преноса (такође познат као Преграда за 'напонског односа') овог кола је једноставно:
У принципу ова функција преноса је комплексих, рационална функција од фреквенција.
Примери[уреди | уреди извор]
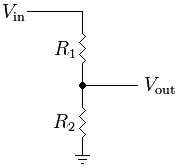
Отпорни разделник је случај где су обе импедансе, Z1 and Z2, су чисти отпорници (слика 2). Заменом Z1 = R1 and Z2 = R2 у претходном изразу даје:
Ако R1 = R2 онда
Ако Vout=6V and Vin=9V (оба најчешће користе напон), онда:
и решавањем користећи алгебре, R2 мора бити двоструко вредност R1. Да бисте решили за R1:
Да бисте решили за R2:
Сваки однос Vout/Vin веће од 1 није могуће. То је, користећи отпорнике камоли то није могуће или обрнути напона или повећавају Vout преко Vin.
Ниско-фреквенцијски филтар RC[уреди | уреди извор]

Узмите у обзир разделник који се састоји од отпорника и кондензатора као што је приказано на слици 3. Поредећи са општим случајем, видимо Z1 = R and Z2 је импеданса кондензатора, дао
Где је XC реактансе од кондензатора, C је капацитивност од кондензатора, ј је имагинарна јединица, а ω (омега) је угаона фреквенција од улазног напона. Овај разделник ће онда имати однос напона:
- .
Производ τ (tau) = RC се зове временска константа кола. Однос затим зависи од фреквенције, у овом случају опадања као фреквенција повећава. Ово коло је, у ствари, основни (првог реда) нискофреквенцијски филтер. Однос садржи имагинарни број, а заправо садржи и амплитуду и фазна информационог филтера. Да бисте издвојили само амплитуде однос, израчунати на магнитуда од односа, то је:
Индуктивни разделник[уреди | уреди извор]
Индуктивни Стаклене разделник AC улаз према индуктивности: Једначина је за не-интеракцију индуктора, узајамна индуктивност (као у аутотрансформаторu) ће изменити резултате. Индуктивни Стаклене поделити ДЦ улаз према отпорности елемената као за ресистиве делитеља изнад.
Капацитивни разделник[уреди | уреди извор]
Капацитивни разделник не пролази ДЦ улаз. За АЦ улаз једноставна једначина је капацитивна: Било која струја цурења у цапацтиве елементима захтева употребу генерализованог израза са две импедансе. Избором паралелног R и C елемената у одговарајућим пропорцијама, иста подела однос може да се одржава преко корисног распон фреквенција. Ово се принцип примењује у плаћеним осцилоскопским сондама за повећање пропусног опсега мерења.
Ефекат учитавања[уреди | уреди извор]
Излазни напон од напона разделник није фиксна већ варира у зависности од оптерећења. Да бисте добили разумно стабилан излазни напон излазна струја треба да буде мали део улазне струје. Мана овога је да је већина улазне струје се губи у облику топлоте у делитеља. Алтернатива је да користите регулатор напона.
Апликације[уреди | уреди извор]
Напонснки разделници се користе за подешавање нивоа сигнала, пристрасности активних уређаја појачалима, и за мерење напона. Витстонов мост и мултиметар оба укључују напона преграде. Потенциометар се користи као променљиве напона разделник у контроли запремине радио. Напонски разделници се такође може користити да би микроконтролер за мерење отпорност сензора.[1] Сензор је повезао у напона разделник поред познатог отпорника, а познато улазни напон је дат, а излазни напон се мери, а затим се користи за одређивање отпор сензора.
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
Литература[уреди | уреди извор]
- Horowitz, Paul; Hill, Winfield (1989). The Art of Electronics. Cambridge University Press.
Спољашње везе[уреди | уреди извор]
- Voltage divider and current calculator with variable count of resistors
- Voltage divider or potentiometer calculations
- Voltage divider tutorial video in HD
- Online calculator to choose the values by series E24, E96
- Online voltage divider calculator: chooses the best pair from a given series and also gives the color code
- Java based search tool for analysing a potential divider circuit
- Voltage divider theory - RC low-pass filter example and voltage divider using Thévenin's theorem

















