Сабирач (електроника)
У електроници, сабирач је дигитално коло које врши сабирање бројева. У многим рачунарским и другим процесорима, сабирачи се не користе само у аритметичко-логичкој јединици већ и у другим деловима где је потребно израчунати адресу, индексе табеле и сличне операције. Иако сабирачи могу бити конструисани за много репрезентација бројева, као што су бинарно кодовани децимални бројеви или код више 3, најчешће се праве сабирачи који оперишу са бинарним бројевима. У случајевима где се за представљање негативних бројева користе комплемент двојке или комплемент јединице, сабирач се лако може модификовати да врши одузимање, односно да постане одузимач. Другачије представљање означених бројева захтева комплексније сабираче.
Полусабирач (HA - half adder)[уреди | уреди извор]
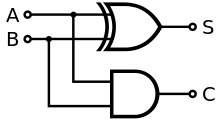
Полусабирач сабира две једноцифрене бинарне вредности A и B и као резултат враћа, такође, две вредности, суму (S) и пренос (C). Сигнал за пренос презентује величину преноса која се јавља уколико на улазу имамо обе 1 (збир износи 2, што у бинарном облику износи 10). Укупна вредност суме је 2C+S. Једноставна конструкција полусабирача, приказана на слици десно, обухвата једно ЕX-ИЛИ коло за S и једно И коло за C сигнал. Додавањем једног ИЛИ кола за комбиновање њихових излаза за пренос, два полусабирача чине један потпун сабирач.[1]
Једноставније, полусабирач сабира два улазна бита и генерише пренос и суму коју представља на својим излазима.
Потпуни сабирач (FA - full adder)[уреди | уреди извор]

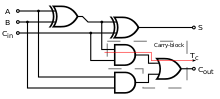
Потпун сабирач' сабира бинарне вредности и генерише вредности које шаље на излаз. Једнобитни потпуни сабирач сабира три једнобитна броја, често означена са A, B, и Cin. A и B представљају операнде, а Cin представља бит преноса претходног сабирача.[2] Потпун сабирач је обично само компонента у каскади сабирача који сачињавају сабирач који оперише са 8, 16, 32 - битним бројевима. Коло производи двобитни излаз, пренос и сума се репрезентују као и код полусабирача са Cout и S где . Истинитосна таблица једнобитног сабирача изгледа:
| Inputs | Outputs | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Комплетан сабирач може бити имплементиран на много различитих начина са транзисторима или логичким компонентама. Један начин је са и .
У оваквој имплементацији, крајње ИЛИ коло, пре бита излаза за бит преноса може бити замењено ексклузивним ИЛИ колом. Једноставно имплементирање се постиже и са само два IC чипа који садрже само једно коло по чипу. У овом случају Cout може бити имплементирано као .
Комплетан сабирач може бити конструисан и помоћу два полусабирача, повезујући A и B на улаз једног полусабирача, односно, њихову суму на улаз другог сабирача, такође, потребно је повезати битове преноса у једно ИЛИ коло.
Комплекснији сабирачи[уреди | уреди извор]
Ripple-carry сабирач (RCA)[уреди | уреди извор]
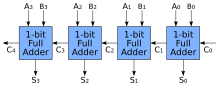
Могуће је креирати логичко коло за сабирање n-битних бројева коришћењем потпуних сабирача. На Cin улаз сваког сабирача доводи се Cout претходног. Овакав сабирач назива се ripple-carry сабирач, јер сваки бит преноса "таласа"(преноси се) до следећег сабирача. Можемо закључити да први(али само први) сабирач може бити замењен са полусабирачем.
Конструкција ripple-carry сабирача је једноставна, што смањује време израде. Међутим, ripple-carry сабирачи су релативно спори јер сваки потпун сабирач мора чекати бит преноса од претходног да би извршио сабирање. Кашњење кола се може лако израчунати посматрањем кашењења кола једног пуног сабирача (сваки потпун сабирач захтева три нивоа логике) . У 32-битном ripple-carry сабирачу налазе се 32 пуна сабирача. Дакле, најгори случај кашњења је 2 (од улаза првог сабирача-полусабирача) + 31 * 2 (за простирања кроз остале сабираче) = 64 кола кашњења. Сабирач сачињен од наизменичних И-ИЛИ-Инверт кола може бити два пута бржи. [3]
Carry-lookahead сабирач (CLA)[уреди | уреди извор]
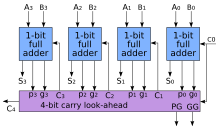
Да би смањили време израчунавања, инжењери су осмислили бржи начин сабирања два бинарна броја познатији као carry-lookahead сабирач. Ови сабирачи раде тако што креирају два сигнала (P и G), за сваку битну позицију, на основу информацији о томе да ли пренос потиче из бита мање тежине(један од улаза износи 1) или се генерише на том месту(оба улаза су 1), или пренос нестаје на тој позицији(оба улаза су 0). У већини случајева P преставља суму излаза полусабирача, а G је излазни бит преноса истог сабирача. Касније, P и G производе пренос за сваку битну позицију. Неке од напредних carry-lookahead архитектура су Manchester carry систем, Brent–Kung сабирач, и Kogge–Stone сабирач.
Неке друге архитектуре вишебитских сабирача су разбијене у блокове. Могуће је мењати дужину блока у циљу побољшања времена извршавања. Ови сабирачи у блоковима укључују carry-skip сабираче, који одређују P и G вредности за сваки блок, и carry select сабирач који прегенерише вредност суме и вредност бита преноса за сваки могући улаз (0 или 1) у блокове. Коришћењем мултиплексора бира одређену вредност када сазна бит преноса.
Lookahead carry јединица (LCU)[уреди | уреди извор]

Комбиновањем више carry lookahead сабирача може бити креиран и већи сабирач. Тако добијен сабирач може се користити на више нивоа да би се направио још већи сабирач. На пример, следећи 64-битни сабирач користи четири 16-тобитна CLA са два нивоа LCU.
Carry-save сабирачи (CSA)[уреди | уреди извор]
Када се јави потреба за коришћењем двооперандских сабирача ради истовременог сабирања три или више операнада, време које протекне збох распростирања бита за пренос мора да се понови неколико пута. Ако је број операнада к, тада се битови преноса морају пропагирати(к-1) пута. Са циљем да се смањи цена која се плаћа због праспростирања битова за пренос, код сабирања већег броја операнада, предлаже се неколико решења (техника). Техника која се најчешће користи је сабирање памћењем преноса (carry save-сабирање). Код овог начина сабирања дозвољава се пропагација преноса само у току задњег корака, док се у свим осталим корацима генерише парцијална сума као и секвенца битова за пренос. На овај начин сабирач са памћењем преноса (CSA) прихвата три n-тобитна операнда и генерише два n-тобитна резулатата, n-тобитну потенцијалну суму и n-тобитни пренос. Други CSA прихвата ове две бит-секвенце, као и други улазни операнд, а генерише нову парцијалну суму и пренос. На овај начин CSA редукује број операнада који се сабирају са три на два без пропагације преноса.
3:2 компресори[уреди | уреди извор]
Можемо посматрати комплетан сабирач и као компресор 3:2: он сажима три једнобитна улазна сигнала и као резултат враћа јединствени двобитни број; то значи да пресликава осам улазних комбинација на четири излазне. Тако, на пример, бинарни улаз 101 резултује на излазу 1+0+1=10 (децимално '2'). Бит преноса представља први бит резултата, док сума представља нулти бит. Исто тако, полусабирач може бити коришћен као 2:2 компресор, компресује четири могуће улазне комбинације на три излазне.
Овакви компресори могу бити коришћени за убрзавање проналажења суме три или више сабирка. Уколико има тачно три сабирка, користиће се carry-save сабирач. Уколико има четири или више сабирака, неопходно је више од једног слоја компресора и постоје различите могућности за дизајн кола: најчешћи су Dadda tree и Wallace tree. Оваква врста кола се пре свега користи у мултипликаторима, због чега се зову и Dadda и Wallace мултипликатори.
Референце[уреди | уреди извор]
- ^ Geoffrey A. Lancaster (2004). Excel HSC Software Design and Development'. Pascal Press. стр. 180. ISBN 9781741251753.
- ^ M. Morris Mano, Digital Logic and Computer Design, Prentice-Hall. 1979. ISBN 0-13-21450-3. стр. 119-123.
- ^ Burgess, N. (2011). Fast Ripple-Carry Adders in Standard-Cell CMOS VLSI (PDF). 20th IEEE Symposium on Computer Arithmetic. стр. 103—111.
Литература[уреди | уреди извор]
- Lancaster, Geoffrey A. (2004). Excel HSC Software Design and Development'. Pascal Press. стр. 180—. ISBN 9781741251753.
- Liu, Tso-Kai; Hohulin, Keith R.; Shiau, Lih-Er; Muroga, Saburo (јануар 1974). „Optimal One-Bit Full-Adders with Different Types of Gates”. IEEE Transactions on Computers. Bell Laboratories: IEEE. C—23 (1): 63—70. ISSN 0018-9340. doi:10.1109/T-C.1974.223778.
- Lai, Hung Chi; Muroga, Saburo (септембар 1979). „Minimum Binary Parallel Adders with NOR (NAND) Gates”. IEEE Transactions on Computers. IEEE. C—28 (9): 648—659. doi:10.1109/TC.1979.1675433. Приступљено 12. 5. 2018.
- Mead, Carver; Conway, Lynn (1980) [December 1979]. Introduction to VLSI Systems (1 изд.). Reading, MA, USA: Addison-Wesley. ISBN 978-0-20104358-7. Приступљено 12. 5. 2018.
- Davio, Marc; Dechamps, Jean-Pierre; Thayse, André (1983). Digital Systems, with algorithm implementation (1 изд.). Philips Research Laboratory, Brussels, Belgium: John Wiley & Sons, a Wiley-Interscience Publication. ISBN 978-0-471-10413-1. LCCN 82-2710.
Спољашње везе[уреди | уреди извор]
- Hardware algorithms for arithmetic modules Архивирано на сајту Wayback Machine (9. април 2007), includes description of several adder layouts with figures.
- 8-bit Full Adder and Subtractor, a demonstration of an interactive Full Adder built in JavaScript solely for learning purposes.
- Interactive Full Adder Simulation, Interactive Full Adder circuit constructed with Teahlab's online circuit simulator.
- Interactive Half Adder Simulation, Half Adder circuit built with Teahlab's circuit simulator.




