Метода половљења интервала

Неколико корака методе половљења интервала, примењеног над почетним интервалом [a₁;b₁]. Већа црвена тачка је нула функције.

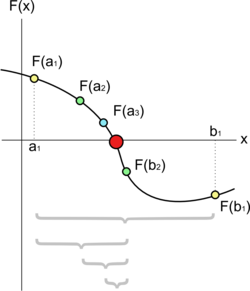
У нумеричкој анализи, метода половљења интервала је алгоритам за приближно решавање једначина, који функционише тако што понавља поступак дељења интервала на пола и избора подинтервала у коме се налази нула функције.

Претпоставимо да желимо да решимо једначину f(x) = 0. Дате су две тачке a и b, такве да су f(a) и f(b) супротног знака. Уколико је функција непрекидна, знамо да она мора да има најмање једну нулу у интервалу [a, b]. Метода половљења интервала дели интервал на два дела рачунајући c = (a+b) / 2. Постоје две могућности: или f(a) и f(c) имају супротне знакове, или f(c) и f(b) имају супротне знакове (претпоставимо да у интервалу постоји само једна нула, и она се не налази у тачки c). Алгоритам половљења интервала се затим поново примењује на подинтервал у коме се промена знака одиграла. Овај алгоритам је по својој природи рекурзиван.

Метода половљења интервала је мање ефикасна од методе тангенте (Њутнове методе), али је мање склона чудном понашању.

Ако је f непрекидна функција на интервалу [a, b] и f(a)f(b) < 0, тада метода половљења интервала конвергира нули функције f. У ствари, апсолутна грешка за методу половљења интервала је највише

${\frac {\left|b-a\right|}{2^{n}}}$

након n корака. Другим речима, грешка се полови у свакој итерацији, па метод конвергира линеарно, што је прилично споро. Са позитивне стране, метод гарантовано конвергира ако су f(a) и f(b) супротних знакова.

Псеудокод

Следи репрезентација методе половљења интервала у Visual Basic коду. Променљиве xL и xR одговарају a и b. Почетне вредности xL и xR морају бити изабране тако да су f(xL) и f(xR) супротног знака (да заграђују корен). Променљива epsilon одређује колико ће резултат бити прецизан.

 'Bisection Method
 
 'Start loop
 Do While (xR - xL) > epsilon
   
   'Calculate midpoint of domain
   xM = (xR + xL) / 2
   
   'Find f(xM)
   If ((f(xL) * f(xM)) > 0) Then
     'Throw away left half
     xL = xM
   Else
     'Throw away right half
     xR = xM
   End If
 Loop

Види још

• Бинарна претрага

Спољашње везе

• Метода половљења интервала на Mathcad Application Server
• Метода половљења интервала
• True example of using bisection method in computer programming free program to isoelectric point calculation

Литература

• Richard L. Burden, J. Douglas Faires (2000), "Numerical Analysis, (7th Ed)", Brooks/Cole. ISBN 978-0-534-38216-2.