Дисекциона слагалица

Дисекциона слагалица, такође звана трансформациона слагалица или Рихтерова слагалица,[1] плочаста је слагалица где сет делова може да се склопи на различите начине да би се направила два или више посебна геометријска облика. Стварање нове дисекционе слагалице се такође сматра дисекционом слагалицом. Слагалице могу да укључују различита ограничења, као што су делови с шаркама, делови који могу да се савијају, или делови који могу да се уврћу. Ствараоци нове дисекционе слагалице наглашавају коришћење минималног броја делова, или стварање нових ситуација, као што је осигуравање да се сваки делић спаја с другим уз помоћ шарки.
Историја
[уреди | уреди извор]Дисекционе слагалице су рана форма геометријских слагалици. Најранији познати описи дисекционих слагалици су из времена Платона (427–347 п. н. е) у старој Грчкој и укључују изазов окретања два једнака квадрата у једном великом квадрату коришћењем четири делића. Друге прастаре дисекционе слагалице су коришћене као графички описивачи Питагорине теореме (трисекција квадрата). Позната старогрчка дисекциона слагалица је остомахион, математичка дисекциона слагалица која се приписује Архимеду, а која подразумева да се два једнака квадрата претварају у једну коцку уз помоћ 14 делића дељењем претходна два делића.
У десетом веку, арапски математичари су користили геометријске дисекције у својим коментарима на Еуклидове елементе. У 18. веку, кинески ученик Таи Чен је описао елегантну дисекцију за апроксимацију вредности броја π.
слагалице су виделе велики пораст у генералној популарности у касном 19. веку када су новине и магазини почели да издају дисекционе слагалице. Најпубликованији креатори слагалици били су Сам Лојд у Америци и Хенри Дудни у Великој Британији. Од тада, дисекционе слагалице се користе као забава и за учење математике, а стварање комплексних дисекционих слагалици се сматра вежбом геометријских принципа од стране математичара и ученика математике.
Типови
[уреди | уреди извор]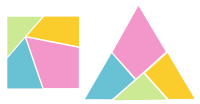

Неки типови дисекционих слагалици су намењени да направе велики број различитих геометријских облика. Танграм је популарна дисекциона слагалица овог типа. Седам делова могу да се конфигуришу у један од неколико основних облика, као што је велики квадрат и правоугаоник у којима су смештени делови, на било који број мањих квадрата, троуглова, паралелограма или езотеричних облика и фигура. Неке геометријске форме се лако стварају, док друге стварају велики изазов. Варијабилност је осигуралла популарност слагалице.
Друге дисекције су намењене да се померају између парова геометријских облика, као што су троугао или квадрат, или квадрат у петокракој звезди. Дисекциона слагалица је по опису хабердашеров проблем, представљен 1907. од стране Хенрија Дуднија. Ова слагалица представља дисекцију троугла и квадрата у само четири дела. То је једна од најједноставнијих и најпознатијих регуларних полигон на квадрат дисекција и данас представља класични пример дисекционих пузили. Није познато да ли је дисекција еквилатералног троугла на квадрат могућа с три делића.
Види још
[уреди | уреди извор]Референце
[уреди | уреди извор]- ^ Forbrush, William Byron (1914). Manual of Play. Jacobs. стр. 315.
Литература
[уреди | уреди извор]- Coffin, Stewart T. (1990). The Puzzling World of Polyhedral Dissections. Oxford University Press. ISBN 978-0-19-853207-1.
- Frederickson, Greg N. (1997). Dissections: Plane and Fancy. Cambridge University Press. ISBN 978-0-521-57197-5.
- Frederickson, Greg N. (2002). Hinged Dissections: Swinging and Twisting. Cambridge University Press. ISBN 978-0-521-81192-7.
- Frederickson, Greg N. (2006). Piano-hinged Dissections: Time to Fold!. A K Peters. ISBN 978-1-56881-299-1.
- Weisstein, Eric W. (2006). „Haberdasher's Problem”. MathWorld. Wolfram Web Resources. Приступљено 8. 8. 2006.
